Пере Грима «Мир математики» № 13 «Абсолютная точность и другие иллюзии. Секреты статистики»
Посвящается Алисии и Пау
Предисловие
Статистика — это наука, которая кажется знакомой. Мы привыкли слышать упоминания о статистике в средствах массовой информации: согласно исследованию (разумеется, статистическому), употребление алкоголя среди молодежи снизилось; результаты опроса показывают, что рейтинг доверия к одному политику выше, чем к другому; партия одержала победу на выборах с перевесом в столько-то пунктов. Даже футбольные комментаторы говорят, например, что, по статистике, одна из команд забивает больше голов во втором тайме. Ответы на вопросы вида «какую информацию можно извлечь из данных» и «какой будет степень достоверности этой информации» не всегда очевидны. Статистику иногда считают несерьезной наукой. Статистические прогнозы не всегда сбываются, и команда, которая, по статистике, всегда забивает гол во втором тайме, в следующем матче может уйти с поля без забитого мяча. В этом заключается разница между статистикой и математикой, которая считается более серьезной наукой. Если футбольная команда «потеряла все математические шансы на победу в чемпионате», это означает, что ей ни при каких обстоятельствах уже не получится стать чемпионом. Статистические данные можно трактовать очень широко, чем активно пользуются политики. Это добавляет штрихи к довольно неприглядному образу статистики в глазах обывателей. Однако статистика применяется намного шире. Она используется в медицинских исследованиях (действительно ли новое лекарство лучше старого), в биологии (сколько особей определенного вида обитает на определенной территории и грозит ли им вымирание), при прогнозировании (сколько электричества будет потрачено завтра), при анализе рынков (какая упаковка больше нравится клиентам), в социологии (что думает молодежь по конкретному вопросу), в экономике (на сколько выросли цены), при анализе технической надежности (с какой периодичностью нужно осматривать детали самолета) и при управлении качеством на предприятиях (на какой проблеме стоит сосредоточить усилия). Возможно, этот перечень слишком велик, но тем не менее он неполон: статистика используется и во многих других областях. Статистика изучает сбор данных (каким должен быть объем данных и в какой форме следует их собирать) и способы их анализа, позволяющие получить ответы на интересующие нас вопросы. Цель статистики — получить знания объективным способом на основе наблюдений и анализа реальности. Именно в этом заключается суть научного метода. В этой книге рассказывается о некоторых наиболее интересных аспектах статистики: как представить информацию с помощью графиков; как избежать пропущенных мячей (продолжим пример с футболом), располагая нужными статистическими данными; как провести сбор данных, чтобы ответить на поставленные вопросы. Мы расскажем о статистических исследованиях, предвыборных опросах и о том, какие рассуждения лежат в основе всех статистических тестов. Мы также совершим экскурс в теорию вероятностей — многим эта тема может показаться сложной и скучной, но в действительности она помогает достаточно просто получить ответы на множество занимательных вопросов. Автор стремился сделать книгу интересной и познавательной. Если мне удалось хотя бы отчасти достигнуть этой цели, за это стоит благодарить моих сокурсников по Политехническому университету Каталонии и увлеченных преподавателей статистики Universidad del Valle в Кали (Колумбия), в частности Роберто Беара. Наконец, я хотел бы выразить благодарность Педро Деликадо, Луису Марко, Лурдес Родеро и Хавьеру Торт-Марторелл за внимательное чтение первого издания этой книги и крайне уместные комментарии и предложения, которые позволили сделать ее намного лучше.Глава 1 Описательная статистика: как извлечь важную информацию из множества данных
Что делать, если перед нами — множество данных, из которых нужно извлечь некую информацию? Вне всяких сомнений, сначала рекомендуется оценить их «на глаз», не просматривая числа одно за другим (наш мозг не способен качественно воспринимать информацию в таком виде), а представив их в виде графиков. Кроме того, можно вычислить некоторые показатели, которые могут быть проанализированы напрямую.Экскурс в историю: эпидемия холеры 1854 года
Сохо — один из самых живописных районов британской столицы. Неотразимая смесь современного и традиционного делает его обязательным местом посещения многочисленных туристов, которые уже много лет гуляют мимо удивительно красивых домов, дают отдых усталым ногам в очаровательных парках, разбитых тут и там среди узких переулков. Учитывая великое множество достопримечательностей и суету, присущую центру любого большого города, вы вряд ли обратите внимание на тщательно воссозданную копию питьевой колонки XIX века, расположенную на углу улицы Бродвик. Однако этот скромный памятник установлен в память о столь важном событии, что он по праву мог бы возвышаться на сотню метров, ярко освещая ночное лондонское небо. Колонка с питьевой водой на улице Бродвик, установленная в 1992 году в честь британского эпидемиолога Джона Сноу, расположена всего в нескольких метрах от другой точно такой же колонки, которая в 1854 году снабжала местных жителей водой из Темзы. В августе того зловещего года в районе Сохо разразилась ужасная эпидемия холеры, от которой всего за три дня умерло больше ста человек, а за две недели — свыше пятисот. Более трех четвертей населения Сохо оставило свои дома, сбегая от болезнетворных паров, которые, как считалось, и были источниками ужасной болезни. Джон Сноу, выдающийся врач, который годом ранее лично дал хлороформ королеве Виктории во время ее восьмых родов, считал иначе. В статье, написанной в 1849 году, он утверждал, что холера передается не через воздух, а через воду. Медицинское сообщество не обратило внимания на его доводы отчасти потому, что в своих рассуждениях Сноу не опирался на какую-то конкретную теорию. Сноу применил целый арсенал разнообразных наблюдений, которые помогли ему установить явную связь между водой и распространением холеры. Он использовал исключительно статистические данные, позволившие обнаружить причинно-следственную связь, которую, как мы уже сказали, он не мог объяснить. Несмотря на это, его наблюдения были столь убедительны и он сумел представить результаты столь удачно, что его современникам не оставалось другого выхода, кроме как признать его правоту. Так началась радикальная перестройка систем водоснабжения больших городов.
В погоне за преступником Холера — это страшное заболевание, основными симптомами которого являются внезапная сильнейшая тошнота и диарея, могущие привести к летальному исходу от обезвоживания. Эпидемию холеры, которая разразилась 31 августа 1834 года, очень быстро стали называть крупнейшей в истории страны. При одном взгляде на цифры волосы встают дыбом: за 72 часа число жертв возросло до 127, большую часть которых составляли дети. Спустя три дня Сноу посетил зону заражения вместе с местным священником Генри Уайтхедом и обнаружил, что большинство умерших жили в домах вблизи колонки с питьевой водой на пересечении улиц Броуд (так в то время называлась улица Бродвик. — Примеч. персе.) и Кембридж. Сноу отметил: «Изучив район, я обнаружил, что почти все смертельные случаи были зафиксированы неподалеку от питьевой колонки на улице Броуд. Всего 10 умерших жили в домах, ближайший источник воды к которым был расположен в другом месте. В пяти из этих случаев жители сообщили, что предпочитали брать воду из колонки на улице Броуд, а не из ближайшей к ним; еще в трех случаях дети — жертвы заболевания проходили мимо этой колонки по дороге в школу». Изучив источник питьевой воды, Сноу не обнаружил заметных следов заражения. Далее он обратился к архивам и составил подробный список всех умерших за последние два дня. Ни один из рабочих пивоварни, расположенной вблизи источника, не заразился, а в приюте для бедняков, также расположенном неподалеку, где проживали более 500 человек, было зарегистрировано лишь пять летальных исходов. Газеты сообщали о новых жертвах эпидемии, проживавших в отдаленных районах: Хампстеде и Излингтоне. Казалось, что Сноу ошибался. Он удвоил усилия: обойдя дом за домом, он убедился, что и в приюте для бедняков, и на пивоварне имелись собственные источники питьевой воды. Одно из семейств, проживавших в Хампстеде, сообщило, что женщина — жертва холеры, ежедневно приносила воду из источника на улице Броуд, так как ей нравился вкус именно этой воды. Племянница этой женщины, также умершая от холеры, поступала аналогичным образом. «А где жила ее племянница?» — нетрудно представить, что Сноу задал именно этот вопрос. «В Излингтоне», — последовал ответ. Сноу записал: «Вывод моего исследования заключается в том, что в этой части Лондона отсутствует вспышка холеры или видимое присутствие заболевания за исключением тех, кто брал воду в упомянутом источнике». Эта простая фраза позднее изменила систему здравоохранения во всем мире. 7 сентября, когда эпидемия все еще не стихла, Сноу добился созыва срочного совещания с местными властями и сообщил им о своем открытии. Он не только выступил с речью, но и представил карту района, на которой отметил численность и место жительства умерших. Карта оказалась настолько убедительной, что уже на следующий день колонка была закрыта. Число умерших резко сократилось, и через некоторое время эпидемия остановилась.
Сила графиков Оригинал карты, составленной Сноу, хранится в Британском музее. В 1855 году улучшенная версия карты была включена в отредактированную статью Сноу, написанную в 1849 году. Фрагмент этой карты приведен на следующей странице. Современному читателю сложно понять, насколько передовым был тогда такой способ представления данных, ведь сегодня он используется повсеместно.

Фрагмент карты района Сохо, где в 1854 году разразилась эпидемия холеры. Источник питьевой воды на улице Броуд обозначен словом PUMP в центре карты. Горизонтальные линии обозначают число умерших в каждом доме.
Умершие от холеры обозначены параллельными отрезками. При нанесении этих обозначений на обычную карту рядом с каждым домом сразу же становится понятно, где располагался очаг эпидемии. Очевидно, что большинство смертельных исходов зафиксировано рядом с источником питьевой воды (pump) на улице Броуд в центральной части карты. Если прибавить к этому скрупулезный труд Сноу по сбору информации, то связь эпидемии с источником питьевой воды не требует дополнительных подтверждений в виде какой-то конкретной теории. Именно так посчитали местные власти и приняли решение закрыть колонку. Очаг заболевания угас, что и стало доказательством того, что холера передается через зараженную воду. Эксперименты, проведенные Луи Пастером в период с 1860 по 1864 год, сыграли ключевую роль в формировании теории патогенов и позволили дать теоретическое объяснение наблюдениям Сноу постфактум. В 1885 году немецкий ученый Роберт Кох установил, что возбудителем холеры является бактерия Vibrio cholerae, и уже в конце века системы водоснабжения большей части крупных европейских городов были заменены. Призрак холеры перестал угрожать половине мира.
Резюмируем данные (1): показатели центра распределения
Описать подозреваемого в преступлении так, чтобы другие смогли гарантированно опознать его, — непростая задача, если только у подозреваемого нет какой-то отличительной черты. Однако эксперты полиции знают, на что следует обращать внимание и какие эпитеты нужно использовать при описании преступника, чтобы другой человек мог себе его представить. Они также знают, как нужно составить фоторобот преступника, чтобы его было легче опознать. Чем-то подобным занимается и статистика. Чтобы обобщить обширное множество данных, рассчитывается несколько показателей (их может быть, например, пять или шесть), которые содержат больше всего информации и помогают получить достаточно точное представление обо всех данных в целом. Эти показатели обычно делятся на три группы: показатели центра распределения, показатели вариации и квантили. В этом разделе мы расскажем о показателях первой группы, которые указывают, в окрестности каких значений располагаются данные.
Среднее арифметическое Мы все рассчитывали свой средний балл, когда учились в школе или институте. Например, баллы выставляются по шкале от 0 до 10, итоговый балл рассчитывается как средний балл трех промежуточных экзаменов, а пороговая оценка равна 5. Оценки 3, 2 и 6 на промежуточных экзаменах означают, что вы не сдали экзамен; оценки 4, 4 и 7 означают успешную сдачу (а как быть, если вы получили 4, 4,3 и 6,3?). Среднее арифметическое — это один из наиболее распространенных показателей центра распределения. Эта величина используется весьма широко благодаря своим особым свойствам и простоте расчетов. Она также демонстрирует нетривиальные свойства при некоторых расчетах. Попробуем, к примеру, найти среднее арифметическое средних арифметических. Среднее арифметическое (3, 4, 3) равно 4, среднее арифметическое (4, 6) равно 5, но среднее арифметическое всех этих чисел равно 4,4, а не среднему значению средних арифметических (4 + 5)/2 = 4,5. Как правило, если дано множество из n1 значений со средним арифметическим и второе x¯1 множество из n2 значений со средним арифметическим x¯2, то средним арифметическим значений множества из (n1 + n2) значений будет

Эта формула эквивалентна формуле расчета среднего для всех значений, так как если выборка содержит n элементов, среднее значение которых равно х¯, их сумма будет равна nх¯. Таким образом, числитель общего среднего арифметического равен сумме всех элементов выборки, а знаменатель — общему числу элементов выборки. Рассмотрим пример. Если средний возраст сотрудников-мужчин в компании равен 36 годам, а средний возраст женщин — 32 годам, то каков средний возраст всех сотрудников? Ответ зависит от конкретной численности мужчин и женщин. Если половина сотрудников — мужчины, а половина — женщины, то средний возраст будет равняться 34 годам. Если 73 % сотрудников — мужчины, а 23 % — женщины, то средний возраст будет равен 35 годам. Заметим, что доля мужчин и женщин рассчитывается по следующим формулам: p1 = n1(n1 + n2) и р2 = n2(n1 + n2), поэтому первую формулу можно записать в следующем виде: x¯t = р1x¯1 + р2x¯2. В некоторых случаях среднее арифметическое является не самой подходящей величиной. Если мы хотим обобщить данные о сроках доставки товара или о времени поезда в пути, среднее арифметическое не даст нам полезной информации. Может быть так, что по договору срок поставки должен составлять 10 дней, при этом в половине случаев товар доставляется за два дня, что становится неожиданностью для заказчика (на складе может не быть места для товара, к примеру), а в другой половине — за 18 (заказчик уже потерял надежду получить товар). Хотя в среднем сроки поставок соблюдаются идеально точно, означает ли это, что в компании все в порядке? Аналогичная ситуация может произойти и в примере с поездом. Если в половине случаев мы будем приезжать на работу на полчаса раньше, это не компенсирует получасовых опозданий во второй половине случаев, особенно если в офис нельзя попасть до начала рабочего дня. В этих примерах наиболее информативной величиной будет процент опозданий или процент случаев, когда поезд опаздывает больше чем на определенное время. Еще один недостаток среднего арифметического — сильная зависимость от крайних значений. Разумеется, странно, что число ног у большинства людей выше среднего, но это на самом деле так: у некоторых людей всего одна нога или нет ни одной (крайние значения), из-за чего среднее число ног у людей чуть меньше двух.
Медиана Медиана — это значение, которое будет располагаться точно в центре, если мы упорядочим значения в порядке возрастания. Если даны значения 6, 7, 5, 2 и 9, их медиана равна 6 — именно это значение расположено в центре упорядоченного ряда из этих чисел. Если число элементов четно, медиана рассчитывается как среднее арифметическое двух центральных элементов. Свойства медианы частично компенсируют недостатки среднего арифметического. Кроме того, она меньше подвержена воздействию крайних значений. К примеру, среднее арифметическое вышеприведенных чисел равно 5,8, медиана — 6. Если при вводе этих чисел в компьютер мы вместо 9 случайно укажем 99, среднее арифметическое станет равно 23,8, а медиана будет по-прежнему равна 6. Еще одним преимуществом медианы по сравнению со средним арифметическим является тот факт, что по определению ровно 50 % значений будут меньше медианы, оставшиеся 50 % — больше. Если, например, мы хотим узнать, входим ли мы в число наиболее высокооплачиваемых сотрудников, нужно сравнить нашу зарплату именно с медианой. Рассмотрим 10 сотрудников с зарплатами 0,8; 0,8; 0,9; 0,9; 1,0; 1,0; 1,1; 1,1; 1,2 и 10 тысяч евро. Все сотрудники, за исключением одного (90 % от общего числа), получают зарплату меньше средней, которая равна 1,88 тысяч евро. С медианой подобное невозможно: если наша зарплата больше медианы, мы гарантированно входим в 50 % наиболее высокооплачиваемых сотрудников. Другой пример. Если для сдачи экзамена нужно набрать 5 баллов и более, а средняя оценка в группе равна 5, мы не знаем, сколько студентов сдали экзамен. Если экзамен сдавали 50 студентов, может случиться так, что 41 студент набрал 4 балла и не сдал экзамен, восемь студентов получили 10 баллов, еще один — 6 баллов. В результате средняя оценка равна 5, хотя распределение оценок в группе действительно немного необычно. Если медиана равна 5, то половина студентов в группе точно сдала экзамен.
Мода Когда речь идет о показателях центра распределения, также всегда упоминается мода. Мода — это значение, которое встречается наиболее часто. В выборке 0, 2, 7, 2, 8, 2, 5, 4 мода равна 2. Ее имеет смысл использовать для качественных показателей. Так, например, если в выборке новорожденных чаще всего встречаются карие глаза, то мода равна карему цвету. Она не содержит какой-то другой информации. Использование моды в этом контексте обусловлено скорее традициями, чем реальной полезностью. * * *
ФЛОРЕНС НАЙТИНГЕЙЛ Летом 1853 года, разбив турецкую армаду, русский черноморский флот был готов захватить Стамбул и взять под контроль пролив Босфор, поставив под угрозу сообщение Великобритании с Индией и нанеся ущерб интересам Франции в Средиземном море. Великобритания объявила России войну, отправив войска на полуостров Крым, где к ним присоединились французская и турецкая армии. Так началась Крымская война, которая завершилась в 1856 году и унесла тысячи жизней. Крымская война считается самой неудачной для британского военного командования. Также это первая война, зафиксированная на фотографиях и в отчетах репортеров. Эта деталь может показаться незначительной, но журналисты в своих статьях рассказывали об ужасающих условиях жизни солдат и бедствиях, вызванных некомпетентностью военного командования. В результате общество возмутилось, и британский военный министр был вынужден отправить на фронт сестер милосердия, во главе которых стояла увлеченная, умная и опытная Флоренс Найтингейл. Прибыв на фронт, сестры обнаружили, что госпитали находятся в ужасном состоянии. Флоренс Найтингейл объяснила, что большинство смертей было вызвано не ранениями, а инфекционными заболеваниями. Она собирала и документально фиксировала данные, которые свидетельствовали о связи между переполненностью госпиталей и уровнем смертности, уделяя основное внимание санитарии, правильному питанию и уходу за ранеными. В течение первых семи месяцев войны, до прибытия Флоренс Найтингейл, раненый британский солдат имел больше шансов выжить, если оставался на поле боя, а не поступал в военный госпиталь. В последние шесть месяцев войны благодаря изменениям в уходе за ранеными смертность снизилась с 40 до 2 %. Флоренс Найтингейл умело отбирала данные, отражающие реальность, и проводила грамотный анализ, чтобы понять суть проблемы и возможные способы ее решения. С помощью статистических исследований и грамотно представленных результатов она смогла преодолеть бюрократию и консерватизм военных и убедить верховное командование в необходимости радикального изменения устройства военных госпиталей. Она спасла множество жизней, а многие процедуры, введенные ею, до сих пор применяются в современных больницах. Флоренс Найтингейл — первая женщина, ставшая членом британского Королевского статистического общества.

* * *
Резюмируем данные (2): показатели вариации
Разумеется, вы слышали шутку: если один человек съел целую курицу, а второй остался голодным, то, по статистике, каждый съел половину курицы. Или если вы положите ноги в холодильник, а голову — в духовку, то средняя температура вашего тела будет абсолютно нормальной. Подобные недоразумения возникают из-за того, что мы хотим обобщить информацию исключительно с помощью средних значений, не учитывая разброс данных. Еще один пример, указывающий на эту же ошибку, — это попытка определить благосостояние жителей страны, учитывая только средний доход на душу населения. Если бы у вас была возможность выбрать, в какой стране родиться, то следовало бы обращать внимание не только на средний доход, но и на его разброс (вариацию). Лучше жить в стране, где каждому гарантирована четверть курицы, чем в той, где в среднем каждому достается половина курицы, но велика вероятность остаться ни с чем. В конечном счете чтобы обобщить информацию, содержащуюся в объемной выборке данных, нужно также измерить их вариацию. Для этого используются различные показатели, о которых мы расскажем далее.
Размах вариации Размах вариации — это разность между наибольшим и наименьшим значением. Например, если дана выборка 2, 6, 7,12,12,18, размах вариации равен 18 — 2 = 16. Этот показатель очень просто вычислить, но он обладает определенным недостатком: в нем не учитывается информация, содержащаяся во всей выборке. Анализ только крайних значений, которые могут встречаться очень редко, явно недостаточен, особенно если выборка велика. Если элементов выборки мало (например, 4–5), размах вариации — подходящий показатель. Если число элементов выборки равно двум, то этот показатель столь же удобен, как и все остальные.
Дисперсия и среднеквадратическое отклонение Наиболее часто используемый показатель вариации — среднеквадратическое отклонение. Чтобы определить его, начнем с дисперсии, так как среднеквадратическое отклонение рассчитывается как квадратный корень из дисперсии. Если бы мы хотели разработать какой-то показатель вариации, то очевидно, что в его расчете должны были бы использоваться все данные, как в случае со средним арифметическим. Например, дана выборка 1, 2, 4, 7 и 9. Можно вычислить среднюю разность между каждым значением и средней величиной, равной 4,6:

Однако этот показатель всегда будет равен нулю вне зависимости от того, какими будут элементы выборки. Следовательно, он не имеет смысла (его значение одинаково вне зависимости от вариации). Используем абсолютные значения разностей:

Этот показатель называется среднее абсолютное отклонение. Он достаточно удобен, так как большему разбросу данных соответствует большее значение этого показателя. Но все же гораздо более интересными свойствами обладает показатель, в котором проблема взаимного сокращения разностей решается путем возведения их в квадрат:

Разность между каждым значением и средним арифметическим 4,6. Дисперсия — среднее значение квадратов этих разностей.
Этот показатель называется дисперсией. Он позволяет оценить разброс значений, а также лежит в основе многих статистических методов. Дисперсия обозначается δ2. Недостаток дисперсии заключается в том, что ее единица измерения — это единица измерения исходных данных, возведенная в квадрат. Если исходная выборка состоит из значений длины в метрах, единицей измерения дисперсии будет квадратный метр, что несколько усложнит интерпретацию. Решение этой проблемы очень простое: нужно всего лишь извлечь из дисперсии квадратный корень. Полученное значение, которое мы будем обозначать δ, называется среднеквадратическим отклонением и является самым распространенным показателем вариации. Обобщение большой выборки данных очень часто производится с помощью всего двух показателей: среднеквадратического отклонения и среднего арифметического. * * *
НЕМНОГО ФОРМУЛ Общая формула расчета дисперсии такова:
где xi — значения элементов выборки, μ — среднее арифметическое, N — число элементов выборки. Формула расчета среднеквадратического отклонения такова:

* * * Коэффициент вариации Какая величина варьируется больше — вес котов или вес коров? Допустим, что средний вес кота равен 4 кг и в 95 % случаев он лежит в интервале от 3 до 5 кг. Предположим, что вес коровы в 95 % случаев лежит в интервале от 480 до 500 кг. Если мы изучим вес котов, то увидим, что он варьируется очень сильно (некоторые коты весят почти в два раза больше других), а вес коров различается несущественно. Среднеквадратическое отклонение веса котов будет находиться в пределах 0,5 кг. В соответствии с закономерностью вариации весов, 95 % выборки отстоит от среднего значения не более чем на два среднеквадратических отклонения. Об этом будет рассказано в следующей главе, посвященной нормальному распределению. Среднеквадратическое отклонение веса коров будет лежать в пределах 5 кг, что в 10 раз больше, однако вес коров варьируется меньше. Чтобы разрешить этот парадокс, возникающий при сравнении вариаций, вводится коэффициент вариации, который равен частному среднеквадратического отклонения и среднего значения:

В нашем примере коэффициент вариации для веса котов равен 0,125, для веса коров — 0,01. Коэффициент вариации — безразмерная величина. * * *
ДВЕ КЛАВИШИ ДЛЯ РАСЧЕТА СРЕДНЕКВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ Несмотря на то что дисперсия и среднеквадратическое отклонение — важнейшие показатели статистики, их часто пытаются скрыть. При попытке обобщить большую выборку данных мы можем столкнуться с одной из следующих ситуаций. 1. Интерес представляют имеющиеся данные. Мы хотим определить среднее значение или среднеквадратическое отклонение этих данных, составляющих так называемую генеральную совокупность. 2. Имеющиеся данные являются выборкой из изучаемой генеральной совокупности. Иными словами, интерес представляет не столько среднее значение или среднеквадратическое отклонение, сколько оценка (некое представление) значений генеральной совокупности. Расчет среднего значения в обоих случаях будет одинаков. Формула не изменится, так как наилучшей оценкой среднего значения генеральной совокупности является среднее значение выборки. Если мы хотим сделать какие-то выводы о генеральной совокупности на основании выборки, необходимо, чтобы выборка была репрезентативной. При расчете дисперсии ситуация выглядит несколько иначе. Если дана генеральная совокупность, то нужно использовать формулу, указанную выше. Если же дана выборка, а мы хотим оценить дисперсию генеральной совокупности, используется следующая формула:
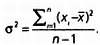
Почему? Дело в том, что при работе с выборками вариация рассчитывается с использованием среднего значения по выборке, а не среднего значения генеральной совокупности, которое мы хотим найти. Можно сказать, что среднее значение выборки подстраивается под данные выборки, что ведет к недооценке вариации генеральной совокупности. При делении на (n -1) результат будет чуть больше, и он будет точнее описывать дисперсию генеральной совокупности. При делении на 4 или на 3 разница окажется большой, но при делении на 100 или на 99 разница будет невелика. На практике для больших объемов выборки подобные расхождения не влияют на результат. Если эта тема кажется вам сложной и вы что-то не понимаете, не волнуйтесь. Если при решении задачи вам придется выбирать между двумя формулами, считайте, что речь идет о выборке. В этом случае нужно делить на (n — 1). Если вы используете статистическую программу, где нет возможности выбора из двух формул, знайте: в программе используется формула для выборки.
х¯ — среднее арифметическое. σn — среднеквадратическое отклонение в случае, когда расчет выполняется для всей генеральной совокупности и интерес представляет среднеквадратическое отклонение «всех» данных. σn-1 — среднеквадратическое отклонение в случае, когда расчет выполняется для выборки и стоит задача оценить среднеквадратическое отклонение всей генеральной совокупности, из которой взята выборка.
Статистические функции на калькуляторе: одна клавиша используется для расчета среднего арифметического, две клавиши — для вычисления среднеквадратического отклонения. * * *
Резюмируем данные (3): квантили
Некоторые показатели используются часто, но они не характеризуют центр распределения и вариацию. С их помощью «проводят границы» на области данных и получают некие эталонные значения, с которыми можно сравнить все остальные.
Квартили Если упорядочить данные по возрастанию, медиана разделит множество данных пополам. Первым квартилем называется медиана первой половины; 25 % значений будут меньше него, 75 % — больше. Медиана второй половины называется третьим квартилем, 75 % значений меньше него, 25 % — больше.

Допустим, что первый квартиль зарплаты в вашей компании равен 1000 евро, медиана — 1300 евро, третий квартиль — 2000 евро. Если вы получаете 800 евро, то находитесь среди 25 % тех, кто получает меньше всего. Если ваша зарплата равна 1500 евро, вы входите в 50 % сотрудников, получающих больше остальных, но минимум 25 % зарабатывают больше вас. Если ваша зарплата равна 2100 евро, вы входите в 25 % наиболее высокооплачиваемых сотрудников компании.
Перцентили 15-я перцентиль — это значение, меньше которого ровно 15 % упорядоченного множества данных. Очевидно, что 85 % значений будут больше него. Если ваша зарплата равна 70-й перцентили, это означает, что зарплата 70 % сотрудников меньше вашей, или, что аналогично, 30 % получают больше вас — если вы из тех, для кого стакан всегда наполовину пуст. Перцентили также используются при оценке результатов тестов на интеллект. Если вы находитесь в 90-й перцентили, это означает, что 90 % участников справились с тестом хуже, чем вы. Многие впервые сталкиваются с перцентилями, когда педиатр говорит, что, например, рост вашего сына находится в 45-й перцентили. Это означает, что 45 % мальчиков (значения для мальчиков и девочек отличаются) того же возраста ниже вашего ребенка. Всемирная организация здравоохранения составляет справочные таблицы и графики, в которых указывается рост детей разного возраста.
Графики роста девочек (вверху) и мальчиков (внизу) в возрасте от 5 до 19 лет, составленные Всемирной организацией здравоохранения, с медианой и 3-й, 15-й, 85-й и 97-й перцентилями.
Проценты: выглядят безобидно, но на самом деле опасны
Чтобы выделить какой-либо важный аспект множества данных, используются проценты («65 % подростков в возрасте от 10 до 17 лет признаются, что пользовались видеоиграми для взрослых»), но в книгах по статистике эта тема не рассматривается: считается, что она либо выходит за рамки статистики, либо слишком проста и поэтому не заслуживает упоминания. Знак процента можно встретить на простейших калькуляторах. Кажется, что процентами может оперировать любой, однако они часто вызывают путаницу, поэтому будет нелишним рассказать о них подробнее.
Общие вопросы Нужно всегда помнить, от какой величины рассчитывается процент. Рассмотрим пример. Гель для душа раньше продавался в бутылках по 750 мл, теперь же — в бутылках по 1000 мл по той же цене. Сколько процентов вы получаете в подарок? Правильный ответ зависит от того, от какого значения будет рассчитываться процент. Мы получаем бесплатно 33 % от исходного объема и 25 % от нового. Также следует различать проценты и процентные пункты. Так, если прибыль предприятия возросла с 2 до 4 %, то говорят, что она возросла на 2 процентных пункта (но не на 2 %!). Аналогично нужно различать проценты от исходной величины и проценты ее изменения. Лучше понять это различие вам поможет следующий пример. Объем продаж в прошлом году составил 10 миллионов евро. Цель на текущий год — увеличение объема продаж на 6 %. Объем продаж в нынешнем году составил 10,3 миллиона евро. На сколько процентов продавец выполнил намеченную цель? Если целью продавца является рост дохода, то она выполнена всего на 50 %. Однако если мы будем считать целевым значением объем продаж в 10,6 миллиона, а фактическим — 10,3, то получается, что цель выполнена на 97,2 %. Операции с процентами также стоит выполнять очень внимательно. 1. Если цена товара увеличилась на 20 %, а затем снизилась на 20 %, каким будет соотношение начальной и конечной цены? Цена товара изменится: она уменьшится на 4 %. Обозначив исходную цену за х, получим, что итоговая цена равна (х + 0,2х) — 0,2(х + 0,2х) = х — 0,04х. 2. Товар состоит из 10 компонентов. Стоимость каждого компонента возросла на 2 %. На сколько увеличится стоимость товара? Она возрастет на 2 %. Цена отдельных компонентов в этом случае не имеет значения. Если вы все еще сомневаетесь, выполните расчеты вручную и убедитесь в этом самостоятельно. 3. Если Иван зарабатывает на 1000 % больше Петра, он получает в 11 раз больше, а не в 10, как может показаться. Если он зарабатывает на 100 % больше, он получает в два раза больше, если на 200 % больше — то в три раза больше.
В действительности всё не так. Парадокс Симпсона Когда приводятся проценты для нескольких групп, каждая из которых разбита на подгруппы, может показаться, что налицо определенная зависимость. Однако истинная зависимость будет прямо противоположной. Это явление известно под названием парадокс Симпсона. Рассмотрим пример. Крупная компания открывает новый завод и создает 250 рабочих мест в службе продаж, монтажа и в складской службе. На рабочие места претендовали 355 мужчин и 325 женщин. Работу получили 190 мужчин (53,5 %) и 60 женщин (18,5 %). Уровень подготовки мужчин и женщин был абсолютно одинаков. Можно ли утверждать, что имеет место дискриминация женщин при приеме на работу? Нет, это не так. Исходные данные таковы:
В действительности процент принятых на работу в каждом отделе выше среди женщин. Причина в том, что в службе, куда было принято больше всего сотрудников, рабочие места получили много мужчин и мало женщин, а в других службах, где требовалось меньше сотрудников, ситуация была обратной. В начале раздела мы приводили цитату о том, что 65 % молодых людей 10–17 лет пользовались видеоиграми для взрослых. Взята она из реального газетного заголовка. В статье объясняется, откуда взята цифра в 65 %: автор сложил положительные ответы 50 % юношей и 15 % девушек! Любопытно, каков был бы результат, если бы на этот вопрос положительно ответили 50 % юношей и 60 % девушек?
Графическое представление переменной
Решим еще одну задачу. Владелец пекарни обеспокоен тем, что, как ему кажется, вес готовых булок различается слишком сильно и некоторые булки могут весить меньше, чем допускается стандартом. Для выпечки используются две печи, в которых выпекают хлеб два оператора. В какие-то дни работает первый оператор, в какие-то — второй. В следующей таблице указан вес (в граммах) для выборки булок. Измерения производились в течение 20 дней:
Вес булки должен равняться (220 ± 10) граммов. Допустим, что представленная выборка является репрезентативной. Нужно ответить на вопросы, действительно ли существует проблема; что происходит; что нужно сделать, чтобы устранить проблему, если она вообще существует. Если вы попытаетесь сделать какие-то выводы «на глаз» на основании данных, представленных в таблице, то, скорее всего, ошибетесь. Хотя речь идет всего о 160 значениях, выводы, сделанные «на глаз», скорее всего, будут неточными. Также не следует погружаться в объемные вычисления или использовать сложные методы. Достаточно представить данные графически, как показано далее.
Гистограмма веса 160 хлебобулочных изделий.
Эта диаграмма называется гистограммой. Она крайне полезна для анализа вариации данных. В нашем примере гистограмма указывает, что проблема действительно существует, так как вес некоторых булок меньше минимально допустимого. Иными словами, речь идет не об исключениях, а о естественной вариации веса булок. На следующих гистограммах представлены данные по каждой печи и по каждому оператору в отдельности. Из них четко видно, что неполадки присутствуют в печи № 2, так как центральное значение на соответствующей диаграмме смещено. С печью № 1 все в порядке, и данные для обоих операторов практически совпадают.

Вес булок для каждой печи и каждого оператора в отдельности.
Даже для очень малого объема данных, например для такого: 21,1; 17,8; 19,7; 18,6; 16,8; 21,7; 28,7; 20,1; 19,5; 17,8, на простой точечной диаграмме видны подробности, которые можно упустить при простом анализе данных «на глаз». В этом случае видно, что одно значение существенно отличается от остальных, и следует проанализировать причины подобного отклонения (возможно, это простая опечатка: оператор ввел 28,7 вместо 18,7). Эти вопросы крайне важны, так как ошибка в исходных данных может перечеркнуть всю проделанную работу.

Представление множества данных с помощью точечной диаграммы.
Если мы хотим учесть порядок выборки данных, гистограммы и точечные диаграммы нам не помогут. Для этого нужно представить данные в виде временного ряда, как показано на следующем рисунке, где четко заметно увеличение среднего роста населения Испании на протяжении XX века. Разумеется, на основе графиков подобного типа нельзя делать экстраполяции: вовсе не факт, что через 1000 лет средний рост будет находиться у отметки 2 м 70 см.

Изменение среднего роста населения Испании в период с 1910 по 1982 год. (Источник: X. Спийкер, X. Перес и А. Камара. Изменение среднего роста населения Испании в XX веке по результатам исследования министерства здравоохранения. Журнал Estadistica Espahola, № 169, 2008 г.)
Помимо стандартных графиков, которые мы только что рассмотрели, круговых и им подобных диаграмм, можно использовать и другие, не столь известные. Существует, например, диаграмма «стебель — листья». Рассмотрим практический пример. Группу из 92 студентов попросили измерить пульс. На гистограмме на следующей странице представлены полученные значения (все данные, использованные в этом примере, содержатся в файлах примеров пакета статистических программ Minitab).

Гистограмма и диаграмма «стебель — листья», на которых представлены данные о пульсе для группы из 92 студентов.
При построении диаграммы «стебель — листья» все значения делятся на две части. Наименее значимая часть (в этом случае единицы) образует «листья», другая (десятки и сотни) — «стебель». Наименьшим значением является 48, далее следует 54 и снова 54, затем три раза 58 и так далее до последнего значения, равного 100. Заметим, что строки диаграммы имеют ту же форму, что и столбцы гистограммы. Следовательно, диаграмма «стебель — листья» содержит информацию, представленную на гистограмме, и кроме этого обладает следующими свойствами. 1. Исходные данные можно восстановить. При взгляде на гистограмму можно увидеть, что существует значение в интервале между 45 и 50, но мы не можем сказать, чему оно равно. В диаграмме «стебель — листья» эта информация не теряется. 2. Диаграмма «стебель — листья» позволяет увидеть детали, которые остаются незамеченными на других графиках. Например, не следует думать, что студенты измеряли свой пульс в течение одной минуты. Если бы это было так, то примерно половина значений были бы четными, а половина — нечетными. Однако мы видим, что все значения четные. Это означает, что студенты измеряли пульс в течение 15 или 30 секунд, а затем умножали результат на 2 или на 4. Результаты, полученные таким образом, имеют большую погрешность по сравнению с результатами, полученными реальным измерением в течение одной минуты. Иногда ученые разрабатывают особые диаграммы для определенных задач. В качестве примера можно привести диаграммы, которыми сопровождаются футбольные трансляции. С помощью ряда переменных на них отображается ход матча, указываются голевые моменты каждой команды, а также другая информация — от числа пасов в штрафную зону до забитых голов и незабитых пенальти.

Ход атак во время футбольногоматча. (источник: Elpais.com)
При построении графиков чаще всего используются компьютерные программы. Это могут быть пакеты статистических программ, программы для работы с электронными таблицами или системы обработки текстов. Текстовый редактор, использованный при написании этой книги, позволяет с легкостью создавать и применять в расчетах диаграммы. С его помощью можно строить красивейшие трехмерные графики или простые плоские диаграммы. Нужно учитывать, что трехмерные диаграммы, как правило, более эффектны, но могут быть менее понятны. Тип диаграммы следует выбирать в зависимости от контекста и из соображений наглядности.

Графики, построенные в текстовом редакторе Word.
В завершение этого раздела, посвященного графическому представлению значений одной переменной, вернемся к нашему примеру с пекарней. Допустим, что в пекарне есть третья печь, для которой также были произведены измерения веса 80 готовых булок (столько же измерений было проведено для печи № 1). Как вы охарактеризуете вариацию веса хлеба, выпеченного в новой печи, по сравнению с печью № 1?

Как вы оцените печь № 3 по сравнению с печью № 1?
Если вам кажется, что вес хлеба, выпеченного в печи № 3, варьируется сильнее, чем вес хлеба, выпеченного в печи № 1, вы ошибаетесь. На обеих гистограммах представлено одно и то же множество данных. Они выглядят по-разному, так как был выбран разный масштаб. Вас сбил с толку выбранный способ представления данных. Мораль: при построении диаграмм для сравнения различных данных убедитесь, что диаграммы имеют одинаковый масштаб. Программа по умолчанию изменяет масштаб с учетом вариации данных. Нужно скорректировать масштаб вручную, иначе диаграммы будут неверно представлять данные и, образно говоря, вы попадете в сети, которые сами же и расставили.
Представление взаимосвязи между двумя переменными
Для представления связи между двумя переменными используются диаграммы, подобные следующей.

Соотношение цены и мощности двигателя 449 автомобилей с дизельным двигателем. (источник: интернет-страница Королевского автомобильного клуба Испании, 10 ноября 2009 г., указанные параметры поиска: седан, дизель, 4 двери)
Можно заметить, что некоторые значения, например 150 л. с., встречаются чаще других. Также можно определить, какие автомобили дешевле аналогов с той же мощностью двигателя. Видна четкая взаимосвязь между переменными, но это не означает, что между ними существует причинно-следственная связь. Например, если мы построим подобный график, демонстрирующий связь ущерба, причиненного пожаром, с числом пожарных, задействованных при его тушении, станет очевидна четкая взаимосвязь: чем больше ущерб, тем больше пожарных, но это не означает, что ущерб причинили пожарные. Другой пример: школьники с большим размером ноги делают меньше орфографических ошибок, чем школьники с меньшим размером. В это трудно поверить, не так ли? Тем не менее чем старше дети, тем больше у них размер ноги и тем меньше они делают ошибок. В обоих случаях существует третья переменная, которая имеет взаимосвязь с двумя рассматриваемыми переменными. В первом случае это масштаб пожара, во втором — возраст школьника. Однако в некоторых случаях причинно-следственная связь не столь очевидна. 28 декабря 1994 года в газете The New York Times была опубликована статья о возможном воздействии на здоровье умеренного потребления вина. Приводилась таблица с указанием среднего уровня употребления вина и уровня смертности от сердечно-сосудистых заболеваний в 21 стране. Эти данные представлены на диаграмме ниже.

Связь смертности от сердечно-сосудистых заболеваний с уровнем употребления вина в 21 стран. (источник: The New York Times, 28 декабря 1994 г.)
Можно заметить, что в странах, где пьют больше вина, уровень смертности от сердечно-сосудистых заболеваний ниже. Но, как мы уже говорили, это не означает, что между этими двумя переменными обязательно существует причинно-следственная связь. Из этой диаграммы не следует, что если мы будем пить больше вина (разумеется, в разумных пределах), то риск инфаркта снизится. Страны, в которых употребляют больше всего вина, одновременно с этим являются его крупнейшими производителями. Это означает соответствующий климат, режим питания, обычаи — какой-то из этих факторов и может быть причиной низкого уровня болезней сердца. Впрочем, причиной действительно может быть умеренное потребление вина, но данные, которыми мы располагаем, этого не доказывают. * * *
ПРОСТЫЕ ДИАГРАММЫ ДЛЯ РЕШЕНИЯ СЛОЖНЫХ ЮРИДИЧЕСКИХ ВОПРОСОВ На президентских выборах в США в 2000 году, когда основными кандидатами были демократ Альберт Гор и республиканец Джордж Буш, их результаты оказались практически равными, что вызвало бурное обсуждение. В штате Флорида, где проживало около 6 миллионов избирателей, Буш одержал победу с преимуществом в 537 голосов. Кандидат, одержавший победу в этом штате, набирал необходимое для победы число голосов и становился президентом. Были поданы протесты, и окончательный вердикт должен был вынести суд. Не вдаваясь в юридические тонкости, приведем диаграмму, на которой отображены голоса, полученные Гором, в сравнении с голосами в пользу другого кандидата, Патрика Бьюкенена, в каждом из 67 округов штата Флорида.

Сравнение голосов в пользу Патрика Джозефа Бьюкенена и в пользу Альберта Гора в каждом из 67 округов штата Флорида. (источник: Д. Мур. Learning from Data. «Statistics: A Guide to the Unknown», 4-е издание)
Первое, что бросается в глаза, — число голосов в Палм-Бич не подчиняется общей закономерности. Вместо закономерных 1500 голосов в его пользу было отдано 3 411 голосов. При взгляде на диаграмму становится понятно, что округ Палм-Бич должен обладать какой-то особенностью. Однако не было никакой причины, по которой Бьюкенен мог бы получить в этом округе значительно больше голосов, чем в остальных. Он сам и его сторонники заявляли, что 1000 голосов будет для них оптимистичным прогнозом. Вскоре стало ясно, что единственной особенностью была форма бюллетеня для голосования, использовавшегося в этом округе. Чтобы проголосовать за выбранного кандидата, нужно было проколоть отверстие в бюллетене. Из-за неудачного дизайна бюллетеней многие избиратели (очевидно, более 2000, достаточно взглянуть на график) проголосовали в пользу Бьюкенена, хотя в действительности хотели отдать свой голос Гору.* * *
Масштаб может быть обманчив
Для конкретного множества данных среднее значение и среднеквадратическое отклонение — это конкретные значения, не допускающие разночтений. Однако в случае с графическим представлением данных это не так. Вид гистограммы для конкретного множества данных будет зависеть от выбранного масштаба (вы уже увидели это на примере печи № 3 в нашем примере с пекарней), а также от ширины интервалов и граничных значений интервалов. К примеру, при неизменной ширине интервалов при границах 190,192,194, … гистограмма будет выглядеть иначе, чем для граничных значений 191, 193, 193, … Например, изменение значений экономического показателя за последние шесть месяцев можно представить графиком, изображенным слева, на котором показан впечатляющий рост, или графиком, изображенным справа, из которого следует, что значение показателя практически не изменилось. Различие между этими графиками заключается в выборе масштаба вертикальной оси.

Одни и те же изменения в разных масштабах.
Изменение масштаба горизонтальной оси также может преподнести немало сюрпризов. На следующем рисунке представлен график изменения объемов продаж за последние четыре года, построенный в мае 2010 года, когда были доступны данные лишь по апрель 2010 года. Это указано в подписи к графику, но создается впечатление, что объем продаж резко упал. В действительности же, учитывая, что на период до апреля включительно приходится треть годового объема продаж, прогнозное значение продаж на 2010 год превышает 150.

Четыре значения несравнимы между собой: за 2010 год доступны данные только до апреля включительно. * * *
КАТАСТРОФА «ЧЕЛЛЕНДЖЕРА» Все мы хотя бы раз видели фотографию космического челнока «Челленджер» на стартовой площадке: шаттл, похожий на самолет, вертикально закреплен на огромном топливном баке, полном горючего, по бокам которого находятся ракетные ускорители, выводящие челнок на орбиту. Эти ускорители, как и другие элементы челнока, невозможно перевозить в собранном виде, поэтому они изготавливаются и доставляются по частям, а сборка происходит на космодроме. Чтобы обеспечить отсутствие утечек в местах стыков и предупредить катастрофу, используются круглые уплотнительные кольца из каучука толщиной 6 мм и диаметром 12 м. В ночь с 27 на 28 января 1986 года группа техников и руководители завода, производившего ракетные ускорители, провели телеконференцию с коллегами из NASA, чтобы обсудить возможность переноса запуска челнока на следующий день. Их беспокоило, что, по прогнозу, температура воздуха в день запуска должна была быть существенно ниже обычной — от 26 до 29 °F (от -2 до -3 °C). Они боялись, что при таких температурах уплотнительные кольца не обеспечат полную герметичность. Имелись данные с прошлых запусков, так как обломки двигателей после каждого запуска собирались и тщательно анализировались. В одном случае были зафиксированы дефекты уплотнительных колец, но серьезных происшествий не было отмечено ни разу. После анализа данных члены рабочей группы сделали вывод, что доказательства того, что низкие температуры могут негативно отразиться на уплотнительных кольцах, отсутствуют. Было принято решение не переносить запуск. Утром следующего дня спустя 59 секунд после запуска сквозь одно из колец, которое было не полностью герметичным, начало прорываться пламя. Огонь быстро достиг топливного бака, что привело к взрыву шаттла и гибели семерых астронавтов, находившихся на его борту. Катастрофа шокировала весь мир и привела к радикальным изменениям в космической программе NASA. Президент Рональд Рейган создал комиссию по расследованию инцидента, куда вошли видные представители научного сообщества. Комиссия определила, что анализ имеющихся данных был недостаточным. Одной из ошибок стало то, что не были приняты во внимание данные о полетах, в которых кольца не были повреждены (рис. 1). Подробный анализ параметров уплотнительных колец во время всех запусков позволил бы увидеть взаимосвязь между отмеченными дефектами и температурой воздуха. На рис. 2 четко видно, что данные, соответствующие температуре в момент планируемого запуска «Челленджера», отсутствуют, следовательно, нельзя гарантировать отсутствие неполадок при этой температуре. Кроме того, можно увидеть, что при понижении температуры число неполадок возрастает. На рис. 3 число колец, на которых были обнаружены дефекты (вне зависимости от их серьезности), заменено оценкой, определенной комиссией по расследованию катастрофы. На этом рисунке связь видна еще более четко. Это наглядный пример того, как с помощью простого графического анализа данных можно получить много информации об анализируемой проблеме.

Рис. 1. Каждая точка обозначает запуск, во время которого были зафиксированы повреждения уплотнительных колец. На вертикальной оси отмечено число происшествий, на горизонтальной — температура во время запуска (в °F).

Рис. 2. На удлиненной горизонтальной оси отмечена прогнозная температура в момент запуска «Челленджера». На графике также содержатся точки, соответствующие запускам, во время которых не было отмечено неполадок уплотнительных колец.

Рис. 3. Для каждого запуска была произведена оценка повреждений уплотнительных колец. Она отложена вдоль вертикальной оси. (источник: Эдвард Тафти. Visual Explanations). * * * Графическое представление данных также может выглядеть по-разному в зависимости от выбранной переменной. Например, если объемы продаж вашей компании падают, что показано на графике слева внизу, можно построить график объема продаж с нарастающим итогом (справа), который, очевидно, будет расти.

Два вида представления информации о продажах: ежемесячном объеме (слева) и объеме с нарастающим итогом (справа).
Не думайте, что графики — это нечто бесформенное и их можно изменять в зависимости от того, какую мысль мы хотим донести. Можно построить наглядные и очень полезные графики, которые помогут с первого взгляда получить всю необходимую информацию, как, например, гистограммы в задаче с пекарней. Графики могут быть запутанными или даже давать ошибочное представление об информации при некорректно выбранной переменной или масштабе. Как правило, внимательность, здравый смысл и немного опыта помогут вам избежать подобных неточностей.
Глава 2 Расчет вероятностей: правила, которые помогут нам в мире неопределенности
Расчет вероятностей вызывает большой интерес у тех, кто полагает, что с помощью науки можно найти стратегию выигрыша в казино, лотереях и различных азартных играх. Однако такие люди вскоре обнаруживают, что теория вероятностей им в этом не поможет. В действительности она играет на руку не игрокам, а создателям азартных игр. Помимо азартных игр расчет вероятностей используется во множестве областей, начиная с медицины, где производится оценка вероятностей при планировании массовой вакцинации, до контроля качества промышленного производства, где порой требуется принять решение о качестве множества деталей на основании результатов испытаний лишь нескольких из них. Математическая теория вероятностей появилась достаточно поздно, уже в XVII веке. Определение вероятности как отношения числа благоприятных исходов к общему числу возможных исходов, данное Лапласом, было сформулировано лишь в 1814 году, хотя Архимед открыл намного менее интуитивно понятную формулу объема сферы за 2000 лет до этого. Длительное время господствовала идея о том, что случайные события непредсказуемы, не подчиняются никаким законам и, следовательно, их анализ неподвластен человеку. Кроме того, считалось, что случайность лежит в области божественного и имеет магический смысл. Поэтому изучение случайных событий длительное время считалось опасным. Одним из первых трудов, посвященных изучению законов теории вероятностей, считается работа Галилея, написанная примерно в 1620 году по заказу некоего аристократа. Он пытался определить наиболее вероятную сумму очков, выпадающую при броске трех игральных костей. Он считал, что чаще всего эта сумма оказывается равной 10 или И, но не был уверен в этом, поэтому решил попросить совета у одного из величайших мудрецов той эпохи. Галилей написал четырехстраничную статью, где изложил свои выводы и размышления. Он рассуждал следующим образом. 1. Игральная кость имеет шесть граней. Руководствуясь соображениями симметрии, мы можем считать, что вероятность выпадения каждой грани одинакова. Следовательно, вероятность того, что выпадет конкретное число, равна 1 к 6. 2. Для каждого из 6 возможных результатов для первой игральной кости существует 6 возможных результатов для второй игральной кости. Всего возможно 36 результатов, приведенных в следующей таблице. Результат броска первой кости обозначен К1, результат броска второй кости — К2.
Все пары очков имеют одинаковую вероятность выпадения, но вероятность выпадения сумм очков различается. Лишь в одном случае из 36 сумма выпавших очков будет равна 2 (если выпадет 1 и 1), и также всего в одном случае сумма очков будет равна 12 (6 и 6). Однако сумма очков будет равна 7 в шести случаях из 36 (то есть в одном случае из 6). Этот результат наиболее вероятен.

Портрет Галилея кисти Тинторетто. Этот итальянский ученый выполнил одно из первых исследований по теории вероятностей.
3. Если мы бросаем не две, а три игральных кости, рассуждения проводятся аналогично. Для каждого из 36 возможных результатов броска двух костей существует 6 возможных исходов при броске третьей кости, поэтому общее число вариантов равно 6·6·6 = 216. На следующей диаграмме изображены частоты для каждого из возможных исходов. В самом деле вероятность выпадения 10 или 11 одинакова: 27/216 = 0,125, вероятность выпадения 9 или 12 несколько меньше: 25/216 = 0,116.

Удивительно, насколько точно игрок предсказал, что вероятность выпадения 10 и 11 очков одинакова и слегка превышает вероятность выпадения 9 или 12 очков.
Расчет вероятностей и статистика
Задачами статистики в прошлом были сбор и описание демографической и другой информации, представлявшей интерес для государства. В XIX веке включение расчета вероятностей в статистику значительно расширило спектр ее возможностей. Страховые компании очень скоро начали использовать статистику смертности и теорию вероятностей, чтобы оценивать ожидаемую продолжительность жизни и точнее определять размеры страховых выплат. Аналогичным образом при прогнозировании исходов выборов и определении степени уверенности в подобных прогнозах используются результаты предвыборных опросов и теория вероятностей. При оценке эффективности нового лекарственного препарата изучается его действие на выборке пациентов, а выводы формируются на основании полученных результатов и с помощью статистических методов, в которых применяются расчеты вероятностей. Однако не нужно быть экспертом по теории вероятностей и необязательно уметь решать сложные задачи, чтобы понимать и применять наиболее распространенные статистические методы. Также не стоит думать, что статистика имеет отношение исключительно к азартным играм и казино. Иногда на обложках книг по статистике мы видим рулетку, игральные кости или колоду карт, хотя уместнее были бы изображения леса, операционных, школ или заводов, ведь именно в этих областях статистика имеет намного более широкое и интересное применение. * * *
АЗАРТНЫЕ ИГРЫ И ПРОИСХОЖДЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ Теория вероятностей стоит особняком не только потому, что она появилась сравнительно поздно, но и потому, что причины ее появления и развития были достаточно необычными. Научные открытия во все времена совершались самоотверженными учеными, которые стремились понять устройство мира и часто жертвовали собой ради блага всего человечества. Однако поводом появления теории вероятностей стало желание людей, ведущих праздную жизнь, определить стратегии выигрыша в азартных играх, которым они посвящали большую часть своего времени. Одна из первых дискуссий, посвященных математической теории вероятностей, зафиксирована в переписке Пьера Ферма с Блезом Паскалем в 1654 году. В ней речь шла о задаче, предложенной философом (и игроком!) шевалье де Мере. В задаче ставился вопрос о справедливом разделении выигрыша в неоконченной игре, если было условлено, что выигрывает тот, кто одержал верх в трех партиях, но игра завершилась со счетом 2:1. Один из вариантов — отдать весь банк тому, кто выигрывал на момент окончания игры, другой — поделить банк поровну. Но и Ферма, и Паскаль сходились на том, что наиболее справедливым будет разделение банка в соотношении 3 к 1 в пользу того игрока, который на момент окончания игры одержал верх в двух партиях.

Обозначим игроков А и В. А выиграл две партии. Рассуждения будут выглядеть так. Допустим, что игроки продолжают игру и вероятность победы в партии составляет 50 % для каждого из них. Возможные варианты окончания игры таковы. 1. Следующую партию выигрывает А. Так как счет станет равным 3:1, игра закончится, победу одержит А, который заберет банк. Вероятность этого исхода равна 0,5. 2. Следующую партию выигрывает В. Счет станет равным 2:2, и игра продолжится. Далее выигрывает А, счет становится равным 3:2 в пользу А, и игра завершается. Вероятность этого исхода равна 0,5·0,5 = 0,25 (выигрывает В, затем выигрывает А). 3. Следующую партию выигрывает В, затем снова выигрывает В. Игра завершается со счетом 2:3 в пользу В. Вероятность этого исхода равна 0,5·0,5 = 0,25.

Подведем итог. Если игра продолжается, то вероятность выигрыша А будет равна 0,5 + 0,25 = 0,75, вероятность выигрыша В будет равна 0,25. В трех случаях из четырех побеждает А, следовательно, будет справедливо, если ему достанется три четверти банка.* * *
Вероятность и ее законы
В соответствии с идеями, которые высказал еще Галилей, если существует n возможных наблюдений, имеющих одинаковую вероятность, и событие А происходит в k из этих наблюдений, то вероятность события А равна:
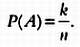
Иными словами,

Например, если в мешке лежит 5 шаров, 3 из которых окрашены в синий цвет, а 2 — в черный, то вероятность вытащить синий шар равна 3/3. Проще не бывает. В некоторых случаях теоретическую вероятность можно вычислить, используя симметрию объекта, от которого зависит результат, как, например, при броске монеты или игрального кубика. Другой подход заключается в том, что вероятность рассматривается как количество наблюдений, при которых произошло событие, при бесконечном увеличении числа наблюдений. Так, чтобы узнать, какова вероятность того, что при броске монеты выпадет решка, нужно бросить монету очень много раз и посмотреть, к какому значению стремится полученное соотношение исходов. Это же верно и в случае с игральными костями. Когда мы говорим, что вероятность выпадения определенного числа очков равна 1/6, мы имеем в виду идеальную игральную кость. Реальная игральная кость может отличаться от идеальной. Некоторые исследователи бросали монету или игральную кость множество раз и записывали полученные результаты. Одним из них был английский математик Джон Керрич, который отбывал тюремное заключение в Дании во время Второй мировой войны. Находясь в тюрьме, он бросил монету 10000 раз, при этом решка выпала 3067 раз, орел — 4933. Соотношение числа решек к числу орлов колебалось так, как показано на следующем графике, на котором приведены не реальные данные, полученные Керричем, а результаты моделирования. По мере роста числа бросков колебания уменьшаются, и разумно предполагать, что соотношение числа исходов стремится к постоянному числу при бесконечно большом числе бросков. Это значение и будет вероятностью выпадения решки при броске этой монеты.

Изменение соотношения числа решек к числу орлов при броске монеты 10 000 раз (результаты получены с помощью моделирования).
Подобные исследования выполнили Жорж-Луи Леклерк де Бюффон, французский ученый XVIII века, который бросил монету 4000 раз (решка выпала 2048 раз), и Карл Пирсон, один из отцов современной статистики, который бросил монету 24000 раз (самостоятельно или с помощью ассистентов), из которых решка выпала 12 012 раз.

Жорж-Луи Леклерк де Бюффон. Портрет кисти Франсуа-Юбера Друз.
Наиболее известный опыт с игральными костями провел в 1850 году швейцарский астроном Рудольф Вольф, который бросил два игральных кубика (один белого, другой красного цвета) целых 20000 раз. Полученные им результаты приведены в таблице на следующей странице.

Результаты, полученные при бросках монеты, согласуются с предположением о ее сбалансированности (вероятность выпадения решки равна 0,5), однако результаты экспериментов, проведенных с игральными костями, достаточно далеки от теоретических значений. При броске обоих кубиков, и белого, и красного, 3 и 4 очка выпадали заметно реже остальных. Представим результаты эксперимента графически, чтобы яснее увидеть эти расхождения (К = красный кубик, Б = белый кубик). В главе 3 мы поговорим о проверке статистических гипотез и обсудим, допустимо ли в этом случае предполагать, что кубики несбалансированы.

Результаты, полученные при броске красного (К) и белого (Б) кубиков 20 000 раз.
Правило «или» Вероятность того, что произойдет событие А или другое событие В, если оба они не могут произойти одновременно, равна сумме вероятностей этих событий. Например, вероятность вытащить туза, короля, даму или валета из колоды в 52 карты (без джокеров) равна: вероятность того, что вытащенная карта — туз: P(A) = 4/52 вероятность того, что вытащенная карта — король, дама или валет: Р(В) = 12/52 вероятность того, что вытащенная карта — туз, король, дама или валет: Р(А или В) = Р(A) + Р(В) = (4/52) + (12/52) = 16/52
Правило «и» Вероятность того, что произойдет событие А и другое событие В, если они являются независимыми, то есть если одно событие никак не влияет на другое, равна произведению вероятностей этих событий. Например, вероятность того, что при двух бросках игральной кости в первый раз выпадет 3 очка, а во второй 4, равна: вероятность выпадения 3 очков: Р(А) = 1/6; вероятность выпадения 4 очков: Р(В) = 1/6; вероятность того, что при первом броске выпадет 3 очка, а при втором 4: Р(А и В) = (1/6)·(1/6) = 1/36
Подсчет исходов Подсчет благоприятных или всех возможных исходов обычно является самой трудоемкой частью исследования, хотя в некоторых ситуациях подсчеты можно упростить с помощью простых рассуждений или проведя аналогию с похожими ситуациями. Например, пусть нам нужно попасть из пункта А в пункт С, пройдя через В. Пусть из А в В ведут три дороги, а из В в С — две дороги. Сколькими способами можно пройти из А в С? Для каждого из трех возможных путей из А в В существует два пути из В в С. Следовательно, попасть из А в С можно шестью различными способами.
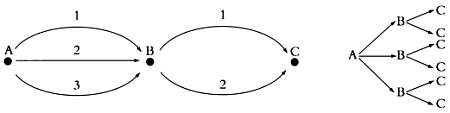
Рассмотрим другой пример, который кажется более сложным. Существует три различных исхода футбольного матча: победа команды хозяев (1), ничья (X), победа команды гостей (2). Какова вероятность угадать исходы всех 14 матчей тура чемпионата? Очевидно, что существует всего один благоприятный исход, единственная выигрышная комбинация. Кажется, что подсчитать возможные случаи сложно, но мы можем использовать тот же принцип, что и при подсчете путей из А в С: первый матч имеет три возможных исхода, каждому из которых соответствует три исхода второго матча. Если бы в туре игралось всего два матча, то общее число исходов равнялось бы 3·3 = 32. Продолжив эти рассуждения, придем к выводу, что число возможных исходов 14 матчей тура равно 314. Вероятность угадать 14 исходов, выбрав их случайным образом, равна 1/314, то есть примерно 1 к 4,8 миллиона. Для решения подобных задач очень полезны формулы комбинаторики. О некоторых из них мы расскажем при решении задач, объясняемых далее.
Применение правил Применим объясненные выше правила на примере. Для этого вычислим вероятность того, что при пяти бросках монеты в произвольном порядке решка выпадет три раза, а орел — два. Как вы вскоре увидите, эта задача намного важнее, чем кажется на первый взгляд. Будем решать ее последовательно. 1. Вероятности выпадения решки или орла при одном броске монеты одинаковы и равны 0,3. 2. Вероятность того, что при двух бросках выпадет решка и решка, равна 0,5·0,5 = 0,25. Мы применили правило «и», так как эти события являются независимыми, то есть выпадение решки в первый раз не увеличивает и не уменьшает вероятность того, что решка выпадет и во второй раз. 3. Вероятность того, что при пяти бросках последовательно выпадут решка, решка, решка, орел, орел, равна 0,5·0,5·0,5·0,5·0,5 = 0,53·0,52 = 0,03125 (мы могли бы записать это число как 0,53, но для понимания будет лучше представить вероятность выпадения орла и решки в виде отдельных сомножителей). * * *
ФРЭНСИС ГАЛЬЮН И КВИНКУНКС Фрэнсис Гальюн (1822–1911) был разносторонним ученым: сфера его интересов включала антропологию, экономику, философию, метеорологию и статистику. Он был двоюродным братом Чарлза Дарвина. Гальюн отличался целеустремленностью и тягой к знаниям, а доходы семьи позволяли ему полностью посвятить себя занятиям наукой. Он изучал медицину, но почти не практиковал, а получив семейное наследство, отправился путешествовать. Он провел два года в Африке и был награжден за свои заслуги золотой медалью Королевского географического общества. Среди полученных им результатов отметим подробный анализ отпечатков пальцев — именно по рекомендации Гальюна они начали использоваться для опознавания преступников. Эта система применяется и сейчас. Он также изучал механизмы наследственности, заметив, что дети высоких родителей чаще всего также высокие, но не настолько, как родители, и что дети невысоких родителей также обычно низкорослые, но не настолько, как их родители. Этот эффект возврата к среднему значению он назвал регрессией к среднему. Этот новый термин занял важное место в современной статистике. Чтобы наглядно представить вариацию, вызванную случайными причинами, он разработал устройство под названием квинкункс. В это устройство опускались шары, которые затем прокатывались мимо стержней, расположенных в шахматном порядке, сталкивались и случайным образом падали влево или вправо. Окончательное расположение шаров по форме напоминало колокол Гаусса. Квинкункс до сих пор используется для наглядной демонстрации нормального распределения. Компьютерные модели квинкункса можно найти в Интернете.

* * * Мы вычислили вероятность того, что сначала выпадет три решки (Р), затем два орла (О) в таком порядке: РРРОО. Но нам нужно вычислить вероятность выпадания трех решек и двух орлов в произвольном порядке, иными словами, вероятность того, что выпадет последовательность РРРОО, или ООРРР, или РОРОР или любой из вариантов.

Искомая вероятность будет равна сумме вероятностей каждого из этих исходов. Вероятности будут складываться по правилу «или», так как эти события являются независимыми (орел и решка не могут выпасть в одном и в другом порядке одновременно). Так как вероятность выпадения каждого из этих исходов одинакова, мы можем умножить вероятность выпадения орлов и решек в заданном порядке на число возможных вариантов (и здесь нам не обойтись без помощи комбинаторики). Данные n предметов можно упорядочить п\ разными способами. Например, если у нас есть 5 книг и 5 мест на полке, первую книгу можно поставить на любое из пяти возможных мест, вторую — на любое из оставшихся четырех, третью — на любое из трех, четвертую — на любое из двух, а для пятой книги останется только одно место. Таким образом, общее число различных вариантов равно 5·4·3·2·1 = 120. В нашем случае также даны 5 «предметов», но не все они отличаются между собой: у нас есть три предмета, одинаковых между собой, и еще два, одинаковых между собой, поэтому мы можем не учитывать перестановки одинаковых предметов. То есть нам нужно разделить общее число вариантов на 3! и 2!. Общее число исходов, при которых выпадет 3 решки и 2 орла, равно 5!/(3!·2!) = 10 Теперь у нас есть все данные, необходимые для вычисления искомой вероятности. Она равна

Зачем нам знать вероятность того, что при пяти бросках монеты в произвольном порядке три раза выпадет решка? Эта задача сама по себе не представляет большого интереса, но далее мы покажем, что аналогичным способом можно решить много других, очень интересных задач.
У случайности есть имя
29 апреля 2004 года некий читатель обратился в редакцию популярной газеты с вопросом: «Я использовал Excel, чтобы сгенерировать случайные числа с помощью функции «=СЛЧИС ()», но эти числа всегда очень маленькие и почти равны нулю. Мне нужна система, чтобы сгенерировать шесть чисел, не превышающих 49, для простой лотереи». По-видимому, читатель думал, что если число является случайным, то оно не подчиняется никаким правилам. Это не совсем так. Существует несколько видов случайных величин. Они делятся на непрерывные, например вес, длина, плотность и так далее, и дискретные (принимающие одно из множества отдельных значений), например число неисправных деталей в партии, количество автомобилей, приезжающих на заправку ежеминутно, и другие. В действительности существует целый «каталог» различных видов распределения вероятностей. Всякий раз, когда мы имеем дело со случайной величиной, следует определить, не подчиняется ли она какому-то конкретному закону распределения вероятностей. В большинстве случаев это действительно так, и нам не потребуется выводить формулы для расчета вероятностей, среднего значения и других интересных параметров: это уже сделали до нас. Сначала может показаться, что отличить случайные величины от неслучайных непросто, подобно тому как человеку, не знакомому с музыкой, сложно разобраться в разных музыкальных направлениях. Однако несколько практических примеров помогут вам научиться с легкостью их распознавать. Далее мы расскажем о некоторых свойствах и примерах использования трех наиболее известных законов распределения вероятностей. То, что нам уже знакомо: биномиальное распределение С помощью общих правил вычисления вероятностей мы смогли установить вероятность выпадения 3 решек и 2 орлов (в произвольном порядке) при 5 бросках монеты с помощью следующего выражения:

В целом число успешных исходов при выполнении n опытов (вероятность успешного исхода неизменна и равна р) — это случайная величина, которая подчиняется очень известному закону распределения вероятностей. Это распределение называется биномиальным. Если мы сталкиваемся с этим распределением, нам не нужно выводить новые формулы для вычисления вероятностей. * * *
ОДНА ОЧЕНЬ ПОЛЕЗНАЯ ФОРМУЛА Если мы отойдем от конкретных чисел и попытаемся вычислить вероятность выпадения х решек при n бросках, где р — вероятность выпадения решки, (1 — р) — вероятность выпадения орла, мы получим следующую формулу:

Интересно, что ее можно использовать не только для решения задач о броске монеты, но и для любых задач, которые подчиняются нижеприведенной схеме:
* * * Рассмотрим три задачи. 1. При производстве на конвейере выпускается 1 % бракованных деталей. Если детали упаковываются в коробки по 50 деталей, какова вероятность того, что в одной коробке окажутся сразу две бракованные детали? 2. Баскетболист забивает 75 % штрафных бросков. Какова вероятность того, что он попадет 8 раз из 10? 3. В семье четверо детей. Какова вероятность того, что ровно двое из них — мальчики? Что общего у этих задач? Все они следуют описанному нами сценарию, следовательно, их очень легко решить.

Расчеты можно произвести с помощью электронных таблиц. В Excel ответ можно найти, используя следующую функцию:

Последняя переменная, которая следует за вероятностью успеха, указывает, хотим ли мы вычислить только вероятность для указанного числа успешных событий (например, ровно 2 бракованные детали; в этом случае эта переменная равна 0) или же накопленную вероятность (число бракованных деталей равно 2 и менее, в таком случае этой переменной нужно присвоить значение 1).

В задаче про игрока в баскетбол мы предполагаем, что вероятность попадания со штрафного броска постоянна, то есть не зависит от давления зрителей, нервов или хода игры (одно из преимуществ хорошего игрока — сохранять процент попаданий неизменным вне зависимости от этих условий). Многие думают, что в задаче о сыновьях и дочерях наиболее вероятно, что в семье два мальчика и две девочки, однако вероятность этого исхода равна всего 38 %. Наиболее вероятным (62 %) является любое другое сочетание. От числа погибших от удара копытом лошади в прусской армии к числу забитых мячей в чемпионате Испании по футболу: распределение Пуассона Если переменная подчиняется биномиальному закону распределения, можно подсчитать, сколько раз она примет определенное значение (число качественных и число бракованных деталей). Эта переменная также будет иметь предельное значение: число качественных деталей не может превышать общего числа деталей в партии. Иногда мы сталкиваемся с переменными, которые обозначают число событий, произошедших в единицу времени или на единицу площади. Такие переменные не имеют верхней границы, по крайней мере с теоретической точки зрения. К классическим примерам подобных переменных относится число посещений интернет-страницы в день, число поломок лифта в год, число звонков на АТС в час и, разумеется, число писем, ежедневно приходящих вам по электронной почте. К примерам событий, происходящих в пространстве, можно отнести следующие: число точек, пораженных ржавчиной, на метр проволоки, число дефектов на квадратный метр (или 10 квадратных метров) ткани, число изюминок в ложке с хлопьями, которые вы едите на завтрак. В 1837 году французский математик Симеон Пуассон решил найти способ изменить формулу биномиального распределения так, чтобы ее можно было применить к подобным ситуациям. Он открыл любопытное выражение, в котором для расчета вероятности любого числа событий достаточно знать лишь среднее число событий (λ). Формула вычисления вероятности того, что некое событие произойдет х раз, выглядит так:


Французский математик XIX века Симеон Пуассон.
Так, если лифт ломается в среднем два раза в год (λ = 2), вероятность того, что в течение года он не сломается ни разу, такова:

Если на интернет-страницу в среднем заходит 100 посетителей в день (будем считать, что число посетителей неизменно в любой день недели, хотя очевидно, что будет существовать определенная разница между рабочими и выходными днями), то вероятность того, что в конкретный день страницу посетит менее 80 человек, такова:

Выполнять расчеты по этой формуле не очень удобно, но нам опять помогут электронные таблицы:

В 1898 году русский экономист и статистик Владислав Борткевич опубликовал книгу, в которой доказал, что распределение Пуассона можно использовать для объяснения статистической закономерности, наблюдаемой при редких событиях. Он использовал данные о самоубийствах и несчастных случаях со смертельным исходом, но самым известным примером его работ является анализ числа солдат, умерших от удара копытом лошади в 14 корпусах прусской армии за 20 лет (с 1875 по 1894 год).

Владислав Борткевич, русский статистик, открывший новые способы применения распределения Пуассона.
В следующей таблице фактическая частота соответствует числу армейских корпусов, умноженному на число лет (14·20 = 280). Среднее число умерших за год в пересчете на один корпус равно (91 + 2·32 + 3·11 + 4·2)/280. Используя это значение в вышеприведенной формуле, получим теоретические значения частоты, приведенные в таблице.

Если мы хотим найти более современный пример, то можно рассмотреть число голов, забитых командой во время футбольного матча. Эта переменная прекрасно соответствует требованиям распределения Пуассона: события происходят в течение четко обозначенного периода времени (футбольного матча), предельного числа событий не существует, а число незабитых голов подсчитать нельзя. Так, на диаграмме слева представлено число голов, забитых каждой командой в каждом из 380 матчей испанского чемпионата 2008–2009 годов. На диаграмме справа представлены данные, вычисленные по нашей формуле.

Фактическое и теоретическое (вычисленное по модели Пуассона) распределение числа мячей, забитых каждой командой в 380 матчах сезона 2008–2009 чемпионата Испании по футболу.
Диаграммы очень похожи. Модель Пуассона хорошо объясняет изменение числа мячей, забитых командой в течение матча.
Колокол Гаусса, или нормальное распределение Колокол Гаусса встречается в математике очень часто. Его форма соответствует форме гистограммы, на которой представлено большое множество значений, подчиняющихся так называемому нормальному распределению. Например, мешки с сахаром весом 1 кг весят не ровно 1000,000… г — некоторые весят немного больше, другие — немного меньше. Подобное колебание веса неизбежно. Оно вызвано множеством незначительных факторов, по отдельности незаметных, но в сумме имеющих ощутимый эффект. На диаграмме ниже показано, что большинство значений находятся вблизи центрального значения, и по мере удаления от него соответствующие значения встречаются всереже и реже. Это классический колокол Гаусса, или диаграмма нормального распределения.

Возможное распределение фактического веса мешков с сахаром весом 1 кг. Диаграмма имеет форму колокола Гаусса.
Математическое выражение, описывающее форму этого колокола, впервые получил французский математик Абрахам де Муавр в 1733 году. Однако эта диаграмма носит имя немецкого математика Карла Фридриха Гаусса, который использовал ее в 1809 году в своей теории ошибок измерения, в частности ошибок, возникающих при астрономических наблюдениях. Гаусс показал, что вне зависимости от расстояния до измеряемого объекта и от его размеров при повторении измерений в одних и тех же условиях полученные значения будут распределяться особым образом. Однако нормальное распределение занимает в статистике особое место не только потому, что оно используется в теории ошибок, но и потому, что оно очень часто встречается в природе.

Портрет Гаусса на банкноте в 10 немецких марок. В центре изображена диаграмма нормального распределения.
Говоря об истоках современной статистики, следует упомянуть имя бельгийского ученого Адольфа Кетле (1796–1874), который в XIX веке провел множество исследований, стремясь обнаружить статистические закономерности, которым подчиняется число преступлений, количество новорожденных, умерших и так далее. В поиске данных, подчиняющихся нормальному распределению, его ждал неожиданный сюрприз: в шотландском журнале были опубликованы данные о росте и охвате грудной клетки более чем 5000 солдат из различных шотландских полков. Эти данные подчинялись тому же закону, что и ошибки астрономических наблюдений.

Адольф Кетле, один из крупнейших статистиков XIX века.
По словам самого Кетле, «если неподготовленный человек измерил бы одного солдата 5738 раз, то результаты не распределились бы столь равномерно… как результаты 5738 измерений шотландских солдат. Если бы нам представили два ряда чисел, не снабдив их какими-либо комментариями, мы бы могли с уверенностью определить, какой ряд чисел соответствует результатам измерений 5738 разных солдат, а какой получен в результате неумелых измерений единственного солдата». * * *
ЗАКОН ЭПОНИМОВ СТИГЛЕРА Многие законы, теоремы, заболевания, научные открытия и постоянные носят имена их первооткрывателей. Так, известны болезнь Альцгеймера, постоянная Эйлера, великая теорема Ферма, комета Галлея и колокол Гаусса. Название события или закона по имени человека называется эпонимом. Стивен Стиглер, преподаватель статистики Чикагского университета и известный историк статистики, открыл закон, который вкратце звучит так: «Ни одно открытие не носит имя того, кто в действительности его совершил». Если говорить об упомянутых нами примерах, то болезнь Альцгеймера, названная в честь Алоиса Альцгеймера, была описана до него минимум пятью учеными. Постоянная Эйлера была открыта Якобом Бернулли, великая теорема Ферма в действительности не теорема, а гипотеза Ферма, а доказал ее Эндрю Уайлс в 1995 году. Комета Галлея была известна астрономам еще до Рождества Христова, хотя именно Эдмунд Галлей вычислил ее орбиту и предсказал дату ее возвращения. Если говорить о статистике, то нормальное распределение и диаграмма в форме колокола были открыты и подробно описаны не Гауссом, а французским математиком Абрахамом де Муавром, который опубликовал свои труды по этой теме в 1733 году, почти на 80 лет раньше Гаусса. Это не означает, что одним ученым незаслуженно достаются лавры других. Некоторые совершают важный вклад в науку или объясняют уже открытое, но не очень известное явление, и по этой причине имена этих ученых остаются в истории. Профессор Стиглер опубликовал статью, посвященную этой теме, но он был не первым: до него об этом писали многие другие ученые, в частности Роберт Мертон, которого нередко цитирует Стиглер. Получается, что закон Стиглера подчиняется сам себе.

Портрет Абрахама де Муавра, который открыл так называемый колокол Гаусса за много лет до этого знаменитого немецкого математика. * * *

«Живая» гистограмма. Каждый человек стоит в колонне, соответствующей его росту. (источник: Эдвард Тафти. Наглядное отображение количественной информации. Цитируется работа Brian L. Joiner «Living Histograms», опубликованная в 1975 году в журнале International Statistical Review.)
Есть и еще одна причина, по которой нормальное распределение играет столь значительную роль. Очень часто в статистических исследованиях основное внимание уделяется средним значениям: анализируется средняя урожайность в зависимости от использованного удобрения, среднее значение выборки сравнивается с предполагаемым средним значением генеральной совокупности и так далее. Средние значения варьируются в зависимости от того, каким образом была взята выборка. Их вариацию на практике можно описать с помощью закона нормального распределения, даже если исходные данные генеральной совокупности не подчиняются этому закону. Например, число очков, выпадающее при броске игральной кости, совершенно не подчиняется закону нормального распределения. Это дискретное распределение с шестью возможными значениями: 1, 2, 3, 4, 5 и 6. Вероятность выпадения каждого из них одинакова. Если мы бросаем два кубика и анализируем среднее число выпавших очков, то частота выпадения различных средних значений уже не будет одинаковой. Наиболее вероятно, что среднее значение будет равно 3,5. Если мы бросаем четыре кубика, то столбиковая диаграмма, представляющая вероятность возможного среднего числа выпавших очков, будет напоминать колокол Гаусса. Если мы будем бросать 10 кубиков, что равносильно взятию выборки величиной 10, то на диаграмме будет очевидно вырисовываться колокол Гаусса. Таким образом, распределение средних значений подчиняется нормальному закону.

Распределение средних значений стремится к нормальному, хотя исходные значения не подчиняются нормальному закону.
Тем не менее хотя этот закон распределения встречается очень часто, название «нормальный» — не самое удачное: можно подумать, что остальные чем-то необычны. Однако это название используется повсеместно, при этом некоторые предпочитают назвать его гауссовым распределением. Если исходные данные по своей природе подчиняются нормальному закону (это также можно проверить графически или с помощью тестов), то их распределение полностью описывается всего двумя величинами: средним арифметическим, которое определяет центр колокола Гаусса, и среднеквадратическим отклонением, которое определяет форму колокола.

Среднее значение и среднеквадратическое отклонение — две величины, характеризующие нормальное распределение.
Если вес мешков с сахаром подчиняется нормальному закону, среднее значение равно 1000 г, среднеквадратическое отклонение — 5 г, то можно рассчитать, сколько мешков будут иметь вес свыше 1010 г, сколько — от 995 до 1010 г или менее 995 г. До недавнего времени для этого требовалось выполнять расчеты и сверяться со специальными таблицами (которые до сих пор включаются в некоторые учебники по статистике), но сегодня все расчеты можно выполнить автоматически с помощью электронных таблиц Excel. Например, вероятность того, что мешок сахара весит меньше 995 г, равна

Заметим, что приблизительно 16 % мешков имеют вес менее 995 г, но о весе конкретного мешка ничего определенного сказать нельзя. По этой же причине можно говорить об ожидаемой продолжительности жизни населения, но не о конкретной дате смерти отдельного человека. Также существуют правила, основанные на том, что вне зависимости от среднего значения (μ, читается «мю») и среднеквадратического отклонения (σ, читается «сигма») 68 % значений будут лежать в интервале μ ± σ, 95 % — в интервале μ ± 2σ, 99,7 % — в интервале μ ± 3σ. Так, в прошлом примере среднее значение μ = 1000, среднеквадратическое отклонение σ = 5. В интервале 995—1005 будет лежать 68 % результатов. Следовательно, в этот интервал не попадает 32 % значений, по 16 % с каждой стороны. Это означает, что 16 % мешков будут иметь вес меньше 995 г.

Это правило также можно использовать для интерпретации среднеквадратического отклонения. Если мы рассмотрим распределение роста людей, среднее значение может равняться 170 см. В этом случае среднеквадратическое отклонение должно лежать в интервале 6–7 см, так как 1 или 2 % населения гарантированно имеют рост выше 190 см. Следовательно, это значение превышает среднее на три среднеквадратических отклонения.
Другие виды распределения. Рассуждения о «теоретических» моделях Существуют и другие законы распределения вероятностей. Например, если случайная величина является непрерывной и все ее значения равновероятны, распределение называется равномерным. Когда мы используем функцию «=СЛЧИС ()» в Excel для генерации случайных чисел, результаты подчиняются именно этому закону. Существует много других законов распределения. На следующей иллюстрации показаны законы распределения, включенные в пакет статистических программ Minitab.

Распределения вероятностей, для которых можно вычислить вероятности напрямую с помощью пакета статистических программ Minitab.
Однако не следует путать модель с реальностью. Например, сфера очень часто встречается во Вселенной, но не существует объектов идеально сферической формы. Зачем же тогда нужны формулы вычисления площади поверхности или объема сферы? Они позволяют получить достаточно точные значения для применения на практике. Это же справедливо и для законов распределения вероятностей. Один из самых часто используемых примеров нормального распределения — распределение роста людей. Однако если мы возьмем точные данные о росте миллиона взрослых жителей нашей планеты, то увидим, что они не подчиняются нормальному распределению с абсолютной точностью. Этого не произойдет и в том случае, если мы разделим людей на группы в зависимости от пола, расы и других характеристик. Нормальное распределение — это качественная модель, которая позволяет с достаточной степенью точности оценить рост людей. Тем не менее это всего лишь модель, которая не полностью соответствует реальности. Это же справедливо и для других законов распределения вероятностей, так как на практике гипотезы не выполняются с абсолютной точностью. Все эти законы описывают лишь теоретические модели (определение «теоретическая» для модели является излишним), которые тем не менее крайне полезны.
Занимательные задачи: удивительные вероятности
Задачи теории вероятностей могут быть достаточно сложными, даже несмотря на относительную простоту формулировки (какова вероятность того, что в выигрышной комбинации национальной лотереи встретятся два последовательных числа?). Интерес представляют необычные вероятности, которые часто противоречат тому, что подсказывает нам интуиция. В то же время сложные задачи нетрудно решить, применив немного воображения. Рассмотрим несколько примеров.
Ложноположительные результаты обследования При медицинском осмотре у человека нашли заболевание, которое встречается всего у 1 % населения. В 5 % случаев результат обследования является ложноположительным (обследование показывает, что человек болен, когда в действительности он здоров). Какова вероятность того, что этот человек действительно болен? Вы можете подумать, что ответ — 95 %, но это неверно. Истинная вероятность намного меньше. Из каждой 1000 результатов 50 являются ложноположительными (5 %), 1 — истинно положительным. На каждый 51 положительный результат приходится лишь один истинно положительный. Значит, вероятность того, что пациент действительно болен, равна всего 1/51, то есть немного меньше 2 %.
Задача о днях рождения В группе 30 студентов. Какова вероятность того, что два студента или более отмечают день рождения в один и тот же день? Многие считают, что эта вероятность невелика, но в действительности она не настолько мала, как может показаться. Сначала нужно вычислить вероятность того, что два человека родились в разные дни. Первый из них может родиться в любой день года (365 благоприятных исходов из 365 возможных), второй может родиться в любой день за исключением того дня, в который родился первый (364 благоприятных исхода из 365 возможных):

Аналогично можно вычислить вероятность того, что три человека родились в разные дни:

Вероятность того, что все 30 студентов родились в разные дни, будет равна:

Существует всего два возможных случая: либо все студенты родились в разные дни, либо минимум двое из них родились в один и тот же день. Следовательно, вероятность того, что как минимум два студента празднуют день рождения в один и тот же день, равна

* * *
СОВПАДАЮЩИЕ ДНИ РОЖДЕНИЯ Это может показаться удивительным, но вероятность того, что в группе из 23 человек двое или более отмечают день рождения в один и тот же день, немного больше 50 % (вероятность равна 50,7 %). Если приведенные рассуждения кажутся вам неубедительными, рассмотрим разные группы из 23 человек. Проблема заключается в том, как найти такие группы людей и узнать дату рождения каждого из них. Тем не менее эту проблему можно решить. На футбольном поле одновременно находятся 23 человека (11 + 11 + 1 судья). Стартовые составы команд и даты рождения всех игроков нетрудно найти в Интернете. Сказано — сделано[1]. Рассмотрим матчи первого тура первого дивизиона чемпионата Испании по футболу 2010 года (матчи игрались 3 января). Из 10 матчей в 5 на поле выходили игроки, отмечающие день рождения в один и тот же день, а именно:

Однако не стоит думать, что если вероятность равна 50 %, то на 10 исходов обязательно будет приходиться 5 благоприятных, ведь при 10 бросках монеты решка необязательно выпадает 5 раз. Вероятности таковы:

* * * В группе из 30 человек двое или больше родились в один день с вероятностью порядка 70 %. В группе из 23 человек эта вероятность несколько больше 30 %, в группе из 40 человек она составляет порядка 89 %.

Вероятность того, что в группе людей два человека или более родились в один день, зависит от размера группы.
Возможен и другой вариант этой задачи, обратный исходному: какова вероятность того, что в группе из 30 человек два человека или более умрут в один день (но необязательно в один и тот же год)?
Выигрышная комбинация выпадает дважды Рассмотрим еще один удивительный пример из теории вероятностей. Один человек всю взрослую жизнь (допустим, 30 лет) играет в лотерею. Если каждую неделю разыгрывается два тиража, какова вероятность того, что за этот период одна и та же выигрышная комбинация выпадет больше одного раза? Существует множество различных лотерей, но, как правило, выбираются 6 чисел от 1 до 49. Число возможных комбинаций в тираже равно 13 983 816 (это число сочетаний из 49 по 6), и лишь одна является выигрышной. Допустим, что этот человек играет 100 раз в год, 3000 раз на протяжении всей жизни. Задача аналогична задаче о днях рождения, только в этом случае в «году» 13983816 дней, а группа состоит из 3000 человек, каждый из которых родился в один из этих дней. Какова вероятность того, что два человека или более родились в один и тот же день? Применив формулы из предыдущей задачи (здесь нам не обойтись без электронных таблиц), получим, что искомая вероятность равна 59 %. Поэтому неудивительно, если за этот период одна и та же выигрышная комбинация действительно выпадет дважды.
Последовательные числа в билетах национальной лотереи В завершение этого раздела попробуем ответить на вопрос, которым вы наверняка задавались. Какова вероятность того, что в выигрышной комбинации лотереи выпадут два последовательных числа? Она намного выше, чем может показаться, и равна 49,5 %. Вычислить точное значение с помощью формул комбинаторики не так-то просто, но порядок этой величины можно оценить с помощью Excel. Для этого нужно выполнить следующие действия. 1. Расположить числа от 1 до 49 в столбце А. 2. Поместить случайные числа в столбец В. 3. Упорядочить столбец В, после чего порядок чисел в столбце А также изменится. 4. Числа в столбце А упорядочены случайным образом. Скопируйте первые шесть значений в столбец С. Эти числа составят выигрышную комбинацию. 5. В столбец D поместите 15 абсолютных значений разницы между числами выигрышной комбинации. В столбце F на следующем рисунке представлены формулы, по которым рассчитываются значения в столбце D.

6. В первую строчку столбца Е поместите наименьшее значение из столбца D. Если это значение равно 1, это означает, что выигрышная комбинация содержит последовательные числа.
Выполнив эти действия, измените порядок чисел в столбце В, что снова повлечет изменение порядка чисел в столбце А. Результатом будет новая выигрышная комбинация, и все остальные числа пересчитаются автоматически. Excel удобен тем, что можно выполнить все необходимые действия один раз, а затем нажать клавишу F4, и все действия выполнятся заново. Можно проверить, что число 1 встретится в столбце Е примерно в половине случаев. Если вам знаком какой-либо язык программирования, вы можете написать небольшую программу для симуляции розыгрыша лотереи и подсчитать, сколько раз выпадут последовательные числа. Также можно обратиться к результатам прошлых тиражей. Результаты испанской национальной лотереи опубликованы на странице Государственной организации лотерей (www.onlae.es). Начиная с первого розыгрыша, о котором имеются данные, прошедшего 17 октября 1985 года, до 31 декабря 2009 года было проведено 2245 тиражей, в 1148 из которых (50,14 %) в выигрышной комбинации встречаются последовательные числа. Последний аккорд: 22 августа 2002 года выигрышной комбинацией была последовательность 13, 21, 24, 26, 32 и 34. 10 декабря 2009 года… точно такая же! Это не так уж удивительно — вероятность подобного совпадения в 2245 тиражах равна 16,5 %.
Глава 3 Как представить целое, зная лишь его часть
Одна из наиболее типичных задач статистики — сделать выводы о целом на основании данных о его части. Это целое называется генеральной совокупностью. Генеральная совокупность может представлять собой множество рыб в озере, множество изделий, выпущенных заводом за последний год, множество жителей, имеющих право голоса на ближайших выборах, или множество людей, страдающих от определенного заболевания. Тщательное изучение генеральной совокупности возможно крайне редко. Опросить всех избирателей, чтобы узнать, за кого они будут голосовать на следующих выборах, нереально и также нереально опросить всех, кто болеет определенной болезнью, чтобы узнать, как подействовало новое лекарство. Конечно, если нас интересует прочность изготовленных изделий, которую нельзя определить, не разрушив изделие, то можно разрушить все произведенные изделия, чтобы определить прочность каждого, но такой подход не выглядит самым разумным. Вместо этого изучается часть генеральной совокупности, которая называется выборкой. На основе результатов, полученных при изучении выборки, оцениваются характеристики генеральной совокупности. Правила вычисления вероятностей позволяют нам получить информацию о качестве этой оценки с помощью ряда понятий, в частности «доверительный интервал» и «предельная ошибка». Очевидно, что наши выводы будут справедливы тогда и только тогда, когда выборка будет репрезентативной. Если она не является репрезентативной, то очевидно, что по ней нельзя будет сделать какие-либо выводы о генеральной совокупности. В некоторых источниках повышенное внимание уделяется математическим аспектам (так как использование непонятных математических терминов — эффектный, хотя и дешевый прием), а способ формирования выборки не указывается. Правильное формирование выборки — достаточно дорогостоящий процесс, но этот аспект крайне важен, так как именно он гарантирует корректность выводов.
Оценка параметров генеральной совокупности с помощью репрезентативной выборки.
Сколько рыб в озере? Сколько машин такси в городе?
Далее мы рассмотрим два примера оценки параметров генеральной совокупности, в частности ее размера, с помощью выборок.
Рыбы Подсчитать, сколько всего рыб в озере, непросто, особенно если озеро большое, а вода в нем мутная. Тем не менее биологи знают, как решить эту задачу. Разумеется, для этого нужно использовать методы статистики. Очень часто используется так называемый метод двойного охвата, который заключается в следующем. 1. Нужно выловить некоторое количество рыб, пометить их и выпустить обратно в озеро. Разумеется, ловить рыбу нужно так, чтобы не поранить ее. Для этого рыбу можно оглушить электрическим током. Метка не должна влиять ни на подвижность рыбы, ни на ее выживаемость. Также необходимо, чтобы метка сохраняла длительную устойчивость к воздействиям среды. 2. Должно пройти некоторое время (порядка нескольких дней), чтобы помеченные рыбы распространились по всему озеру. Затем нужно заново выловить определенное количество рыб (именно в этом заключается суть метода двойного охвата), необязательно такое же, как в первый раз. 3. Нужно произвести расчеты: если в озере N рыб, а мы пометили М из них, то соотношение помеченных рыб к общему их числу равно M/N. Объем повторно взятой выборки, которую можно считать репрезентативной выборкой рыбы в озере, равен С. Из С выловленных рыб R помеченных. Разумно предположить, что доля помеченных рыб во второй выборке равна доле помеченных рыб в озере, иными словами,

Таким образом, примерное число рыб в озере N равно

Рассмотрим пример с конкретными числами. Сначала вылавливается и помечается М рыб (их можно считать случайной выборкой из N рыб, обитающих в озере). В нашем случае М = 13.

Мы выжидаем некоторое время, чтобы помеченные рыбы равномерно распределились по всему озеру, и вылавливаем С рыб, из которых R имеют метку. В нашем случае С = 15, R = 3.

Произведем вычисления. Число рыб в озере примерно равно: N = M·C/R = 15·15/3 = 75

Но что означает «примерно равно»? Если вы подсчитаете число рыб на рисунке в нашем примере, то увидите, что их всего 67. Следовательно, погрешность в расчетах составляет 12 %. Эта ошибка больше или меньше, чем следовало ожидать? Какова возможная величина ошибки при использовании этого метода? Статистика отвечает на эти вопросы, используя разумные предположения и математические инструменты. Однако чтобы получить достаточно точный результат, мы можем прибегнуть к помощи небольшой компьютерной программы, моделирующей вылов рыбы из озера. Мы можем повторить вышеописанные действия произвольное число раз и на основе примерной оценки числа рыб, полученной при каждом моделировании, оценить величину ошибки и частоту, с которой они возникают. Если мы будем использовать те же числа, что и в нашем примере, то увидим, что в 85 % случаев число помеченных рыб во второй выборке будет варьироваться от 2 до 5. Используя выведенную нами формулу, получим, что число рыб в озере лежит в интервале от 45 до 112. В 15 % случаев число рыб будет лежать вне этого интервала.

Распределение числа помеченных рыб в повторной выборке (моделирование было выполнено 10 000 раз).
Оценка числа рыб бывает чаще избыточной, чем недостаточной. Среднее оценочное значение 82 также больше фактического числа рыб в озере. В этом случае говорят, что оценка является смещенной и не отражает истинного значения оцениваемой величины. Оценка существенно улучшится, если внести в формулу небольшие изменения. Проблема в том, что объяснить, почему следует внести именно эти поправки, достаточно сложно.
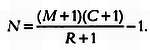
Выполнив расчеты с помощью этой формулы, получим, что если в повторной выборке встретилось 2 помеченных рыбы, то оценка общего числа равна 85, если число помеченных рыб равно 5, то оценка общего числа равна 42. Следовательно, в 85 % случаев оценка численности рыб будет лежать в интервале от 42 до 85. Кроме того, в 27 % случаев число помеченных рыб будет равно 3, что соответствует числу в 64 рыбы, и это очень близко к истинному значению. Эта оценка является несмещенной: если мы повторим вышеописанные действия множество раз, то средняя оценка будет совпадать с истинным значением. Также можно ввести поправочные коэффициенты, если вы считаете, что вероятность вылова разных рыб отличается, метка влияет на выживаемость рыб или метка может стираться. Эта тема очень подробно изучена и описана в книгах по экологии. Также это прекрасный пример того, как статистика может решать задачи, которые кажутся крайне сложными или вовсе невозможными.
Такси Подсчитать число такси в городе намного проще, чем количество рыб в озере. Можно начать с поиска этой информации в Интернете. Так, например, на сайте администрации крупного города может быть указано, что общее число выданных лицензий равно 10481. Каждая лицензия соответствует одному автомобилю. Задача решена.

Однако если эта информация недоступна в Интернете, можно воспользоваться методами статистики. Номер лицензии написан на каждом автомобиле такси. Максимально возможным номером является число выданных лицензий. Когда мы покупаем новый автомобиль, нам выдается новый номер (следующий за последним выданным), а номер старого автомобиля уничтожается. Однако с номером лицензии такси дело обстоит иначе (возможно, с некоторыми исключениями): число лицензий фиксировано, и если кто-то хочет приобрести ее, то может купить только у одного из ее нынешних обладателей. Номер лицензии при этом не изменится. Это значительно упрощает подсчеты. Не пользуясь ни телефоном, ни Интернетом, постояв в центре города всего 10 минут, можно очень точно определить число такси в городе. Посмотрим, как это делается. Допустим, мы выбрали из генеральной совокупности следующие значения: 8, 14, 22, 27 и 35. Попробуем оценить число элементов генеральной совокупности на основе этой выборки. Оно будет однозначно больше 25, так как выборка содержит число 35, и крайне маловероятно, что оно будет равно 1000, так как все пять случайно выбранных элементов генеральной совокупности достаточно невелики. Точная оценка будет примерно равной 40 или 50. Первое правило для оценки числа элементов генеральной совокупности может быть таким: общее число элементов в два раза больше среднего значения минус 1. Например, если генеральная совокупность состоит из 10 элементов 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10, то среднее значение будет равно 5,5, а общее число элементов — 2·5,5–1. Если x¯ — среднее значение генеральной совокупности из N последовательных чисел, начинающихся с 1, то всегда выполняется следующее соотношение: N = 2x¯— 1 Если мы применим эту формулу к вышеприведенным данным о выборке, получим, что ее среднее значение равно 21,2, а примерное число элементов генеральной совокупности составит 2·21,2–1
 41. Эта оценка очень близка к той, что мы предположили изначально.
Однако эта формула имеет один очень важный недостаток. Предположим, даны числа 3, 4, 6 и 15. Их среднее значение равно 7, а оценка общего числа элементов равна 13. Это очевидно неверно, так как выборка содержит число 15, следовательно, генеральная совокупность содержит минимум 15 элементов. Забавно, что результаты, полученные с помощью сложных методов, нередко противоречат элементарному здравому смыслу. Нужен иной способ. В действительности, чтобы определить общее число элементов совокупности в нашем примере, достаточно знать, сколько значений больше 35.
41. Эта оценка очень близка к той, что мы предположили изначально.
Однако эта формула имеет один очень важный недостаток. Предположим, даны числа 3, 4, 6 и 15. Их среднее значение равно 7, а оценка общего числа элементов равна 13. Это очевидно неверно, так как выборка содержит число 15, следовательно, генеральная совокупность содержит минимум 15 элементов. Забавно, что результаты, полученные с помощью сложных методов, нередко противоречат элементарному здравому смыслу. Нужен иной способ. В действительности, чтобы определить общее число элементов совокупности в нашем примере, достаточно знать, сколько значений больше 35.
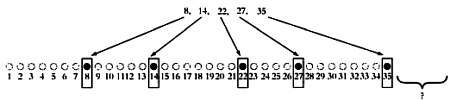
Достаточно разумный вариант — руководствуясь соображениями симметрии, предположить, что после последнего элемента находится столько же элементов, сколько перед первым. В нашем примере мы сложим 7 и 35 и получим примерное число элементов генеральной совокупности — 42. Этот метод неудобен тем, что мы не учитываем элементы, расположенные между элементами выборки. Между тем всегда следует использовать всю доступную информацию. Для этого мы добавим к последнему значению в выборке среднее расстояние между элементами выборки (первое расстояние будет равно числу элементов совокупности перед первым элементом выборки).

В нашем случае это среднее расстояние будет равно: (7 + 5 + 7 + 4 + 7)/5 = 6 Следовательно, оценка общего числа элементов совокупности равна 41. Пусть х1, x2…, хn — значения, расположенные на 1, 2, n-м местах. В этом случае среднее расстояние, которое нужно прибавить, будет вычисляться по формуле:

Нетрудно видеть, что эта формула равносильна следующей: (xn/n) — 1 Следовательно, более точную оценку общего числа элементов генеральной совокупности можно вычислить по формуле:

Насколько точна эта оценка? С помощью методов математической статистики можно доказать, что она является максимально точной из возможных. На языке специалистов такая оценка называется равномерно несмещенной оценкой с минимальной дисперсией. Таким образом, нам достаточно записать номера лицензий 20 такси, прибавить к наибольшему из них его же значение, поделенное на 20, и вычесть 1. В нашем примере, если число лицензий равно 10481 и они пронумерованы последовательными числами, то в 95 % случаев оценка, выполненная по этой формуле, будет лежать в интервале от 9175 до 10990. Очевидно, что этот метод подходит не только для подсчета числа такси в городах. Его также можно использовать, например, чтобы определить число участников массового забега, если всем им выданы последовательные номера. Службы разведки в прошлом посредством похожих методов оценивали вооружение врага. Мы знаем, что оружие имеет табельный номер, поэтому достаточно каким-то образом заполучить лишь несколько единиц, чтобы оценить общее количество оружия.
Какова доля домохозяйств, подключенных к Интернету?
Сначала нужно уточнить определения: что мы будем считать домохозяйством и подключением к Интернету. Нет смысла производить подробные расчеты, если нам неизвестно точное значение используемых понятий. В одном газетном заголовке утверждалось, что половину сигарет выкуривают люди с психическими расстройствами. Это звучало так, будто половина курильщиков — ненормальные, что выглядит явным преувеличением. Однако в тексте заметки под психическим расстройством понималась зависимость от какого-либо вещества, поэтому не половину, а почти все сигареты выкуривают люди, страдающие от никотиновой зависимости, следовательно, имеющие «психическое расстройство». Многие слова, которые мы произносим в повседневной жизни, неоднозначны. Одно из таких слов — «семья». Что такое семья? Муж, жена и их дети? А если вместе с ними живут бабушка и дедушка, их следует считать членами семьи? Достаточно странно определять принадлежность человека к семье по тому, в каком доме он живет. Семью можно понимать и в более широком смысле, как, например, на свадьбах, где «семья невесты» и «семья жениха» насчитывают по несколько десятков гостей. * * *
ОЦЕНКА ВЫИГРЫШНОЙ КОМБИНАЦИИ НАЦИОНАЛЬНОЙ ЛОТЕРЕИ Нам прекрасно известно, что все числа национальной лотереи выпадают с одинаковой вероятностью. Но что можно сказать о среднем значении чисел выигрышной комбинации? 7 января 2010 года выигрышная комбинация испанской национальной лотереи состояла из следующих чисел: 19, 24, 25, 38, 43 и 49, их среднее значение равно 33. В субботу, 9 января, выпали числа 13, 26, 29, 30, 31 и 43; их округленное среднее значение равно 29. Все ли средние значения выпадают с одинаковой вероятностью или некоторые из них встречаются чаще, чем другие? Определенные средние значения действительно встречаются чаще, поскольку, как мы объяснили в предыдущей главе, средние значения подчиняются закону нормального распределения. На следующей гистограмме представлено среднее значение чисел выигрышных комбинаций всех лотерей, начиная с 17 октября 1985 года и заканчивая 31 декабря 2009 года:
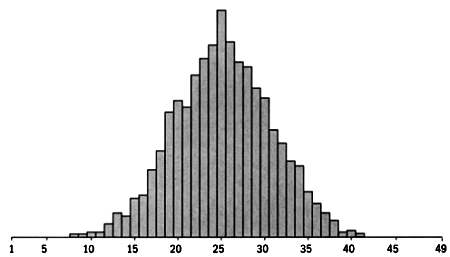
Средние значения чисел в выигрышных комбинациях.
Среднее значение будет с намного большей вероятностью лежать между 20 и 30, чем между 5 и 15. Почему бы нам не выбирать только те комбинации, в которых среднее значение чисел лежит в промежутке от 20 до 30? Ведь таких комбинаций намного больше, и вероятность того, что одна конкретная комбинация окажется выигрышной, всегда одинакова. Иными словами, если в розыгрыше участвует 1000 номеров, то какое число выпадет с большей вероятностью: лежащее в интервале от 500 до 550 или же число, лежащее вне этого интервала? Очевидно, что с большей вероятностью выпадет число вне этого интервала, но это не означает, что конкретное число внутри этого интервала выпадет с меньшей вероятностью, чем конкретное число вне этого интервала.* * * Равносильны ли понятия «дом» и «домохозяйство»? Очевидно, нет, так как если в доме никто не живет, он не является домохозяйством. Домохозяйством также нельзя считать дом, где кто-то живет только по выходным или в сезон отпусков. Является ли домохозяйством квартира, где живут студенты в течение учебного года? Связаны ли понятия «домохозяйство» и «семья»? Следовательно, необходимо четко сформулировать, что такое домохозяйство. Определение подключения к Интернету представляет меньше трудностей, так как способ подключения, будь то ADSL-модем или оптический кабель, не имеет значения. Однако некоторые домохозяйства используют незащищенное беспроводное соединение соседей или бесплатное подключение из соседней библиотеки или кафе. Следует ли считать, что эти домохозяйства подключены к Интернету, или же нужно учитывать только тех, кто платит за подключение?
ДОМОХОЗЯЙСТВО, социально-экон. ячейка, объединяющая людей отношениями, возникающими при организации их совместного быта: ведении общего домашнего хозяйства, совместном проживании и т. д. В отличие от семьи, отношения родства или свойства между членами одного Д. необязательны: оно может включать жильцов, пансионеров, прислугу и других, а также состоять из одного человека, живущего самостоятельно.Словарное определение понятия «домохозяйство».
Будем считать домохозяйством дом или квартиру, где большую часть года проживает один или несколько человек, связанных родственными отношениями. Будем предполагать, что домохозяйство подключено к Интернету, если подключение находится под его контролем и может быть отключено или подключено в любой момент. Если мы возьмем выборку в 1000 из 100000 домохозяйств и в нашей выборке 51,9 % домохозяйств будут подключены к Интернету, значит ли это, что точно таким же будет процент для всей генеральной совокупности? Очевидно, что это необязательно так. Если мы сформируем другую выборку, также случайным образом, то результат, вероятно, будет отличаться, например он может быть равен 50,7 или 52,3 %. По этой причине в представление результатов подобных исследований входит не только примерное значение, но и предельная ошибка. Например, результат оценки может быть равен (51,9 ± 2,3) %. Эти 2,3 %, которые мы прибавляем и вычитаем, и называются предельной ошибкой средней величины. Это означает, что мы получили конкретное значение, но не можем быть до конца уверены, что доля генеральной совокупности точно равна этому числу. Теория вероятностей позволяет определить точность, с которой произведена оценка, и вычислить предельную ошибку средней величины (исходные значения подчиняются закону биномиального распределения: мы анализируем конкретное домохозяйство и можем получить один из двух результатов — домохозяйство подключено к Интернету либо нет). Интервал, покрывающий данную величину с заданной надежностью, называется доверительным интервалом. Можно ли гарантировать, что истинное значение будет находиться в границах этого интервала? Опять-таки этого гарантировать нельзя. Предельная ошибка средней величины рассчитывается для определенного уровня надежности. Как правило, надежность принимается равной 95 %. Это означает, что используемый нами метод позволяет найти истинное значение (в данном случае истинную долю домохозяйств, подключенных к Интернету) в 95 % случаев. Однако мы не можем знать, действительно ли истинное значение находится в границах найденного интервала в нашем конкретном случае. Это аналогично тому, что найденный нами интервал нам бы сообщил человек, который говорит правду в 95 % случаев: ему вполне можно доверять, но абсолютную точность этого результата гарантировать нельзя.

Иллюстрация понятия доверительного интервала.
Можно рассчитать доверительные интервалы с надежностью 99 % или 99,9 %. Обычно это не делается, поскольку, учитывая размер выборки, с ростом надежности доверительный интервал расширяется, и нет никакого смысла говорить, что искомая доля лежит в интервале (51,9±40)%: это можно сказать, не проводя вообще никаких вычислений. Если мы хотим повысить надежность оценки, сохранив при этом предельную ошибку на прежнем уровне, то единственным выходом будет увеличение размера выборки (деньги решают множество проблем, и эту в том числе).
«Партия А опережает партию В на 3,6 пункта»
За подобными заголовками в прессе обычно следует примерно такой текст: «Согласно исследованию, проведенному центром X, если бы выборы состоялись сегодня, партия А опередила бы партию В на 3,6 пункта. Три месяца назад ее преимущество было на полпункта меньше. Данные подтверждают, что популярность партии А растет». В примечаниях к этой статье, помимо прочего, упоминается, что предельная ошибка равна ±4,3 %. Поверхностный анализ этих данных показывает, что преимущество партии А вовсе не столь очевидно. Если в пользу партии А проголосовали 41,6 % опрошенных, то при данной предельной ошибке оценка лежит в интервале от 37,1 % до 46,1 %. Если в пользу партии В проголосовало 38 %, то границами доверительного интервала будут 33,3 % и 42,5 %. Следовательно, в соответствии с результатами опроса можно утверждать, что рейтинг партии А равен 39 %, партии В — 40 %. Нет никаких сомнений в том, что если три месяца назад преимущество партии А было на полпункта меньше (по результатам опроса, а не в реальности), это не является доказательством роста популярности партии А.
Вопрос на миллион Очень часто при проведении исследований возникает вопрос: каким должен быть размер выборки, чтобы результатам можно было доверять? Ответ на этот вопрос зависит от нескольких параметров. 1. От желаемой точности результатов, иными словами от допустимой предельной ошибки. Если мы хотим получить результат с предельной ошибкой 1 %, размер выборки должен быть больше, чем при предельной ошибке в 4 %. 2. От желаемой надежности результата. Если нас устроит надежность 80 %, размер выборки будет меньше, чем для надежности в 95 %. 3. От истинного значения оцениваемой доли. На первый взгляд это может показаться странным, но размер выборки действительно зависит от истинного значения оцениваемой доли. Если в генеральной совокупности отсутствует вариация (100 % элементов совокупности равны между собой), для оценки значения будет достаточно одного элемента совокупности. Если, например, все шары в мешке белые или все черные, достаточно вытащить всего один шар, чтобы определить цвет всех шаров. Чем больше вариация, тем больше необходимый размер выборки. В наименее благоприятном случае объем выборки должен равняться 30 % генеральной совокупности. Мы предполагаем, чему равно искомое значение доли. Предпочтительнее дать этой величине оценку сверху. Если нам ничего не известно о генеральной совокупности либо мы придерживаемся консервативных методов, то можно предположить, что искомый объем выборки равен 50 % от генеральной совокупности. Если нам известно, что искомая доля меньше (например, доля домохозяйств, в которых есть факс), то можно предположить, что их доля равна 20 % (фактическое значение гарантированно будет меньше). 4. От размера генеральной совокупности. Если генеральная совокупность мала (допустим, менее 100000 единиц), а допустимая погрешность также невелика (1–2 %), с ростом размеров генеральной совокупности нам потребуется выборка большего размера. Однако для больших генеральных или для погрешности измерения в 5 % и выше влияние размера выборки будет практически незаметным. Эта тема является источником множества недоразумений, и далее мы расскажем о ней более подробно. * * *
РАЗМЕР ВЫБОРКИ Приведем формулу, связывающую всевеличины, необходимые для определения размера выборки:

где: zα/2 — значение, связанное с уровнем надежности. При надежности в 95 % (используется чаще всего) это значение равно 1,96. Иногда используется значение 2, соответствующее надежности 95,5 %. р — оцениваемая доля; q = 1 — р; Е — предельная ошибка; N — размер генеральной совокупности.* * * Теперь вам понадобится только редактор электронных таблиц — с его помощью легко проверить, как будет изменяться размер выборки при увеличении надежности или допустимой погрешности. Также нетрудно видеть, как на размер выборки влияют различные переменные. Можно построить таблицу, подобную той, что приводится ниже, которая уже содержит все необходимые данные.

Таблица, содержащая размеры выборки для надежности в 95 % в наименее благоприятном случае, когда p = q = 0,5.
Сюрприз! Размер выборки почти не зависит от величины генеральной совокупности
Существует несколько весьма распространенных предположений о размере выборки, которые тем не менее полностью ошибочны. Например, результаты опросов иногда ставятся под сомнение, так как «выборка нерепрезентативна, потому что не охватывает даже 10 % совокупности». Подобные цифры, как, например, 10 % в этом случае, выбираются произвольно. Профессор Роберто Беар из Universidad del Valle в Кали (Колумбия) объясняет истинное положение вещей на нескольких наглядных примерах.
Нужно ли солить суп? Мы готовим суп в небольшой кастрюле и, чтобы определить, готов ли он, пробуем его из ложки. Если к нам пришли гости и мы готовим суп в большой кастрюле, значит ли это, что суп нужно пробовать из большой ложки? Разумеется, нет. Мы используем одну и ту же ложку и пробуем суп одинаково, не важно, готовится ли он в маленькой кастрюле или в большой. Размер выборки не зависит от величины генеральной совокупности. Однако вне зависимости от размера кастрюли нужно как следует перемешать суп, чтобы любая выборка содержала одну и ту же информацию. Перед тем как попробовать суп, важнее тщательно размешать его, а не взять ложку побольше. Это очевидно для всех. Также очевидно, что если мы не размешаем суп, то это не исправить, взяв ложку побольше. Если выборка нерепрезентативна, то увеличение ее размера не решает проблему.
Какая у меня группа крови? Чтобы безошибочно определить группу крови человека, достаточно всего одной капли, так как все капли крови человека одинаковы. Однородность совокупности и в этом случае намного важнее размера выборки. И у новорожденного весом чуть больше 2,5 кг, и у его отца, который может весить больше 100 кг, на анализ берется один и тот же объем крови. Однако связь между размером выборки и величиной генеральной совокупности можно оценить не только интуитивно, но и с помощью формулы. Если генеральная совокупность невелика, с увеличением ее размера объем выборки быстро возрастает, однако затем, начиная с определенного значения, он практически не меняется. * * *
ЛЕВШИ ЖИВУТ МЕНЬШЕ (ИЛИ НЕТ?) 4 апреля 1991 года на первой странице газеты Washington Post была опубликована статья об исследовании, согласно которому левши в среднем живут на 9 лет меньше правшей. В исследовании использовались данные о продолжительности жизни левшей и правшей в двух округах штата Калифорния. Правши часто доживали до преклонного возраста, а среди левшей долгожителей было намного меньше. Новость имела значительный эффект, и вскоре появились объяснения этому результату: якобы левши более подвержены определенным заболеваниям и чаще получают серьезные травмы. Одной из причин этому может быть тот факт, что все устройства, которые мы используем ежедневно, предназначены для правшей. Из-за этого левши чаще получают серьезные травмы, попадают в несчастные случаи и, как следствие, живут существенно меньше. Однако в феврале 1993 года в журнале American Journal of Public Health была опубликована обширная статья, подкрепленная множеством источников, и всё сразу встало на свои места: разницу в продолжительности жизни можно объяснить разницей в распределении возраста левшей и правшей. В начале XX века левшей переучивали держать ручку, ложку и так далее в правой руке, поэтому на момент проведения исследования число пожилых левшей было крайне невелико. Следовательно, до преклонного возраста доживали немногие левши — не потому, что они умирали раньше, а потому, что их переучивали и они становились правшами. Эта статья не попала на передовицы газет, подтвердив правило, согласно которому наибольшее внимание приковывают удивительные и неожиданные новости. Этот пример показывает, как просто порой бывает найти правдоподобную причину той или иной закономерности. Вспомним хотя бы об аналитиках, которые объясняют, почему биржевые индексы падают или растут.* * * Для предельной ошибки в 3 % и надежности в 95 % из генеральной совокупности объемом 10 000 элементов достаточно выбрать всего 1000. Начиная с этого значения требуемый объем выборки практически не увеличивается. Для генеральной совокупности из 100 000 элементов потребуется выборка в 1056 элементов, для совокупности из 1000 000 — 1066 элементов, для 50 000 000 — 1068 элементов. И для небольшого города, и для всей страны размер выборки будет одинаков.

Соотношение между размером генеральной совокупности и размером выборки для предельной ошибки в 3% и надежности 95 %.
Но при этом выборка обязательно должна быть репрезентативной. Если суп хорошо перемешать, не имеет значения, из какой ложки мы будем его пробовать.
Сила случая
Иногда в статьях, описывающих результаты опросов, приводятся расчеты погрешности, но не указывается, как формировалась выборка, либо, напротив, приведены все необходимые пояснения, так что очевидно, что выборка производилась не случайным образом. Все математические правила и законы, на которых основаны эти вычисления, выполняются только при условии, что выборка является случайной. В противном случае погрешность будет рассчитана неверно вне зависимости от того, насколько внимательно вы произвели все необходимые подсчеты. Оптимальный способ формирования случайной выборки таков: нужно взять перечень всех представителей генеральной совокупности, случайным образом выбрать определенное число людей, связаться с ними и назначить встречу. Проблема в том, что этот способ ведет к большим затратам. Можно выбрать не людей, а дома, но в этом случае днем мы не застанем тех, кто работает, а вечером они вряд ли согласятся ответить на наши вопросы. Кроме того, если опрос можно производить только вечером, его проведение потребует длительного времени. Преимущество полностью случайных выборок в том, что они позволяют получить очень точные оценки с помощью традиционных статистических методов. Их единственным недостатком является высокая затратность. Существуют и другие способы, каждый из которых имеет свои преимущества и недостатки. Можно использовать районированную выборку; в этом случае генеральная совокупность разделяется на области, после чего выборки берутся из каждой области. Этот вид выборки наиболее эффективен, если вариация значений между областями невысока. Также можно использовать серийную выборку. Ее принцип заключается в том, что выбираются не отдельные люди, а этажи или подъезды, после чего опрашиваются все жильцы. Это дешевле, чем опрашивать отдельных людей, проживающих далеко друг от друга. Компании, специализирующиеся на проведении опросов, знают, как достичь требуемой достоверности экономически выгодным способом. Однако при любых обстоятельствах важно обеспечить репрезентативность выборки, в противном случае фиаско неизбежно.
Опрос, который изменил все опросы: Лэндон против Рузвельта На выборах президента США в 1936 году кандидатом от республиканской партии был Альф Лэндон, кандидатом от демократической партии — Франклин Делано Рузвельт. Уважаемый и влиятельный журнал того времени The Literary Digest, который публиковал точные прогнозы о результатах прошлых выборов, провел крупнейший в истории предвыборный опрос. По почте было разослано примерно 10 миллионов анкет. Адреса были взяты из списков автовладельцев и из телефонных справочников. Было получено 2300 000 ответов, из которых следовало, что победу одержит Лэндон, а соотношение голосов составит 3 к 2 в его пользу. Выборы выиграл Рузвельт, причем с заметным перевесом: он получил 60,8 % голосов. Причиной ошибки стало формирование прогноза на основе нерепрезентативной выборки. В 1936 году автомобили и домашние телефоны были доступны только обеспеченным людям, которые в большинстве своем голосовали за республиканцев. Крупномасштабный опрос завершился не менее масштабным провалом. В то же время компании, незадолго до того основанной Джорджем Гэллапом, удалось предсказать итог выборов, опросив менее 3000 человек, но обеспечив репрезентативность выборки. Урок не прошел даром: теперь опросы больше не проводятся методом «грубой силы», а имя компании Гэллапа стало своеобразным знаком качества.
Жеребьевка при призыве в армию При формировании выборки или выборе единственного числа случайным образом нужно уделять особое внимание деталям, так как в противном случае могут возникнуть непредвиденные трудности. Среди специалистов широко известен случай, произошедший в армии США в разгар войны во Вьетнаме. Во время призыва в 1970 году впервые использовалась жеребьевка: в ящик было помещено 366 капсул, каждая из которых соответствовала определенному дню года. Сначала в ящик поместили 31 капсулу по числу дней в январе, затем — 29 по числу дней в феврале и так далее. Капсулы перемешали и начали вытаскивать из ящика по очереди. Сначала призвали тех, кто родился в день, указанный на первой капсуле, затем — на следующей и так далее. Однако из-за того, что, по-видимому, капсулы плохо перемешали, возникла проблема. Капсулы, соответствующие дням декабря, остались лежать сверху, и их доля в результатах жеребьевки оказалась намного больше, чем можно было бы ожидать при действительно случайном выборе. Капсулы, соответствующие дням января, лежали на дне и были вытащены ближе к концу жеребьевки, поэтому во Вьетнам отправилось намного больше молодых людей, рожденных в декабре, чем рожденных в январе. Средства массовой информации обратили на это внимание, но никаких изменений предпринято не было. В следующем году система была изменена и жеребьевка проводилась действительно случайным образом. В Европе, в частности в Испании, произошел похожий случай. В 1997 году 165 342 юноши достигли призывного возраста, но армии требовалось меньше призывников. 16442 человека оказались «лишними», поэтому была проведена жеребьевка, чтобы определить, кто не подлежит призыву. Каждому призывнику был присвоен номер. Суть жеребьевки состояла в том, что случайным образом определялся один номер, и от призыва освобождался призывник с этим номером, а также 16441 человек, следующий за ним. Однако случайное число в интервале от 1 до 165 342 было выбрано некорректно. Сначала из лотерейного барабана, в котором находилось всего два шара с номерами 0 и 1, был взят шар, определяющий, в каком интервале находится число. Если выпадал ноль, число бралось из интервала от 1 до 99999, если выпадала единица, число бралось из интервала от 100000 до 165342. Выпал шар с номером 1. Далее из второго барабана, где находились шары с номерами от 0 до 9, был взят второй шар под номером 8. Так как этот номер соответствовал числу, превышающему 180 000, из барабана было извлечено еще несколько шаров, пока не выпал шар с номером, не превышающим 6. Была ли допущена ошибка? Разумеется. Вероятность выпадения числа в интервале от 1 до 99999 была той же, что и вероятность выпадения числа от 100000 до 165342, однако первый интервал содержит больше значений, чем второй, из-за чего для одних призывников вероятность избежать призыва равнялась 8,2 %, для других — 12,6 %, что на 50 % больше.
«Неформальные» опросы Профессиональная ассоциация разослала своим членам письма с анкетами, содержавшими вопросы о работе и годовом доходе. Целью исследования было получить данные, которые затем можно было бы использовать при переговорах о размере заработной платы. Участникам требовалось указать тип компании, в которой они работают (международная, семейная, крупная, мелкая, с большими традициями, недавно основанная и так далее), сферу деятельности, должность, время работы на этой должности, в компании, в сфере деятельности вообще и, наконец, величину заработной платы и премий. Участникам опроса также были высланы конверты с обратным адресом для отправки заполненных анкет по почте. Было отправлено 5 000 анкет и получено 357 ответов. Надежность выводов составила 95 %, погрешность — 5 %. Если вы сверитесь со справочной таблицей, содержащей размеры выборок, то увидите, что размер выборки является корректным. Проблема в том, что эта выборка не является случайной. Следовательно, результаты опроса ошибочны. Если отвечают только желающие, то такую выборку нельзя считать случайной. Возможно, что участники опроса, занимающие высокие посты, очень заняты, постоянно находятся в командировках и не имеют времени на участие в опросах. В опросе также не примут участие те, кто поздно возвращается с работы, мало зарабатывает или временно не имеет работы и не хочет возвращаться к этой теме, а также те, структура зарплаты которых не соответствует ни одному из вариантов, предлагаемых в анкете. Таким образом, выборка не является случайной. Значит, мы не можем использовать математические методы, корректные только для случайных выборок. Это же справедливо и для анкет постояльцев отелей, в которых можно оставить отзыв о качестве обслуживания. Эти анкеты заполняют только те постояльцы, которые особенно недовольны обслуживанием, либо те, кто хочет выразить благодарность в письменном виде (а также, возможно, те, у кого достаточно времени на заполнение анкеты). Информация, полученная из этих анкет, поможет определить положительные и отрицательные моменты, но ее нельзя использовать для получения статистических данных, отражающих мнение клиентов в среднем. Если мы выйдем на улицу с микрофоном в руке и камерой на плече, чтобы опросить жителей, а затем представим их мнение в эфире с комментарием «мы вышли на улицы, чтобы узнать, что думают жители о…», это сделает нашу телепрограмму динамичной и интересной, но не поможет узнать истинное мнение горожан в целом.
Да или да? Значение формулировок вопросов Формулировки вопросов, порядок их следования и даже ударение на отдельные слова может повлиять на результат опроса. Если мы косвенно указываем, какой ответ является «правильным», участник опроса, скорее всего, ответит именно то, что мы хотим услышать. Когда автор этой книги и его коллега читали курс лекций по статистике для всех желающих, мы провели опрос среди слушателей, чтобы показать, как формулировки вопросов влияют на результат. Мы сказали, что хотим узнать мнение аудитории о новом законе, касающемся финансирования политических партий, и раздали всем опросные листы. Все листы выглядели одинаково, но в половине листов формулировка одного из вопросов была изменена.

Две формулировки одного и того же вопроса о финансировании политических партий.
Почти все опрошенные ответили «да» вне зависимости от того, какая из двух анкет им была выдана. То есть некоторые согласились с тем, что «крупные финансовые группы не должны вкладывать значительные суммы денег», другие — с тем, что «компании и организации должны иметь возможность вкладывать средства». Как вы видите, предпочтения составителей опроса могут повлиять на формулировки вопросов, что в свою очередь отразится на результатах. Следовательно, важно понимать, в чем заключается вопрос и как именно следует его задать. Также наряду с результатами опроса следует всегда приводить точные формулировки вопросов.
Звонит телефон, но вас нет дома. Телефонные опросы Проведение опросов по телефону — самый простой и удобный способ, хотя очевидно, что и он имеет определенные недостатки. Телефон доступен практически всем, кто проживает в более или менее развитых районах, но молодежь предпочитает пользоваться мобильными телефонами. Очевидно, что их номеров нет в справочниках и они не войдут в число участников опроса. Нужно определить, повлияет ли на результаты опроса тот факт, что в выборку не войдут те, у кого нет домашнего телефона. Также имеет значение, в какое время будет производиться опрос, кого мы будем опрашивать и как будем заменять тех, кто не пожелает участвовать в опросе. Если мы не уделим должного внимания этим моментам, выборка будет недостаточно репрезентативной, что приведет к серьезным ошибкам.
Частный случай: предвыборные опросы
Предвыборные опросы — один из наиболее популярных способов применения статистики (о котором, однако, не все отзываются положительно). Эти опросы стоят особняком, так как приковывают очень большой интерес общественности. К тому же, в отличие от других случаев, в итоге нам становится известно истинное значение величины, которую мы хотим оценить. Проблема заключается в том, что, помимо традиционных сложностей с формированием случайной выборки, существуют и другие непростые моменты. Рассмотрим некоторые из них.
Избиратели постепенно изменяют свой выбор Предвыборные опросы проводятся за несколько дней или даже недель до того, как пройдут выборы. В некоторых странах результаты таких опросов запрещено публиковать в течение определенного периода времени до выборов (в Испании этот срок равен одной неделе). Таким образом, экстраполяция выполняется дважды: в первый раз — когда мы экстраполируем результаты по выборке на всю генеральную совокупность, во второй — когда предполагаем, что в день выборов результаты будут теми же, что и в день опроса. Однако в это время партии проводят предвыборную кампанию, проходят дебаты между кандидатами, могут происходить события, о которых кандидаты выскажутся определенным образом… Все это может повлиять на мнение избирателей, особенно тех, кто в момент опроса еще не определился с выбором.
За кого голосуют те, кто не определился? Избиратели, которые не определились с выбором, представляют проблему для организаторов предвыборных опросов. Их доля нередко составляет от 20 до 50 % опрошенных. В этом случае их мнение определяется по результатам ответов на вопросы вида «Какой партии вы симпатизируете больше?», или «Программа какой партии вам ближе?», или «За какую партию вы голосовали на прошлых выборах?». Эксперт пытается предсказать, за какую партию проголосует участник опроса, который сам пока еще не знает этого. Очевидно, что отнесение голосов не определившихся избирателей в пользу той или иной партии имеет очень большое значение. Эта задача лежит преимущественно в области социологии и политики, а не статистики. * * *
КАК ПОЛУЧИТЬ КОНФИДЕНЦИАЛЬНУЮ ИНФОРМАЦИЮ И НЕ ПОСТАВИТЬ ОПРАШИВАЕМОГО В НЕЛОВКОЕ ПОЛОЖЕНИЕ Когда мы задаем вопросы, которые считаются неэтичными, или же вопросы личного характера, участники опроса редко отвечают искренне. Однако существуют способы получить эту информацию и в то же время сохранить секрет опрашиваемого. Например, допустим, что неудобный ответ — «да». Чтобы участник опроса мог ответить на вопрос безбоязненно, можно действовать так. 1. Опрашиваемый достает карту из колоды. Половина карт — красные, половина — черные. Участник опроса никому не показывает карту и возвращает ее на место. 2. Если он вытянул красную карту, он отвечает «да», если черную — он отвечает на поставленный вопрос. Очевидно, что если он ответит «да», то мы никак не сможем узнать, что произошло на самом деле: возможно, участник опроса вытянул красную карту либо он действительно ответил «да» на неудобный вопрос. Если мы опросим 1000 человек и 612 ответят «да», примерно 500 из них ответят так потому, что они вытянули красную карту, поэтому их ответы следует исключить. Из остальных 500, которые действительно ответили на вопрос, 112 ответили положительно, следовательно, доля ответивших «да» составит 112/500 = 22,4 %.* * * Недостаточно откровенные ответы на вопросы Формулировки вопросов и порядок их следования также имеют очень большое значение. Написание четких и понятных вопросов, которые не наводят на мысль о «правильном» ответе, — непростая задача. Вопросы должны быть составлены грамотно, а сотрудники, проводящие опрос, должны быть хорошо обученными и мотивированными (читай — высокооплачиваемыми). Иногда опросы дают возможность свободного ответа, что делает ответы участников относительно правдоподобными, а число «неопределившихся» уменьшается, так как часть из них, возможно, на самом деле просто предпочитают не распространяться о своем мнении.
От процента голосов к числу кресел в парламенте Во многих случаях по-настоящему важен не процент голосов, полученный партией на выборах, а число кресел, которое эта партия займет в парламенте. Системы, по которым это число рассчитывается в зависимости от процента полученных голосов (как, например, метод д’Ондта), усложняют расчеты. Например, в избирательном округе, где голосованием распределяется пять мест в парламенте, определенная партия получила 32 % голосов, предельная ошибка составила 3 %, надежность — 95 %. Проблема в том, что если партия получит 31 % голосов, то получит одно кресло, если 33 % — два кресла. Эта разница очень важна, но ее нельзя точно определить с помощью данных, которыми мы располагаем. Другая проблема заключается в том, что существует минимальный процент голосов (например, 5 %), дающий право занять места в парламенте. Если, допустим, за какую-то партию проголосовало 4,6 % избирателей, то нельзя точно сказать, имеет ли она право занять место в парламенте. Результат этой партии также повлияет на число кресел, которое будет распределяться между остальными.
Тем не менее законы статистики выполняются При проведении предвыборных опросов точно спрогнозировать результат будущих выборов мешают многие факторы, которые не всегда относятся к статистике (не говоря уже о манипуляциях и заинтересованности организаторов опроса). Было бы полезно определить, насколько часто результаты крупных предвыборных опросов оказываются ошибочными и какова величина ошибки. Как правило, об ошибочных прогнозах говорят больше, чем о точных, подобно тому как в СМИ больше внимания уделяется плохим новостям. Даже в научных кругах более наглядными и показательными считаются именно те случаи, когда прогноз оказывался неточным. Также могут существовать (и существуют) опросы, результаты которых формируются на основе мнений заинтересованных лиц. Цель таких опросов — повлиять на предпочтения избирателей. Хорошим показателем надежности результатов может служить опыт и авторитет организации, проводившей исследование, а также указание на источник, в котором опубликованы результаты опроса. Чтобы охарактеризовать подлинную надежность результатов, одного лишь статистического показателя в 95 % не всегда бывает достаточно.
Глава 4 Как мы рассуждаем, когда принимаем решение. Проверка статистических гипотез
Этот случай произошел в 1920-е годы в Англии, в Кембридже. Несколько преподавателей, их супруги и гости по случаю прекрасной погоды пили чай на открытой террасе. Попробовав чай, одна из присутствующих дам заметила, что вкус меняется, если налить молоко в чай, а не наоборот. Кто-то осторожно возразил, что это маловероятно. Начался спор, в котором стороны прибегали ко всевозможным аргументам из физики и химии: состав напитка не меняется в зависимости от того, что было налито в чашку сначала, чай или молоко; частицы растворялись абсолютно одинаково; перепад температур исключался и прочие многочисленные доводы. Спорящие пришли к выводу: определить, что было налито в чашку сначала, невозможно. Или же… все-таки возможно? Один из присутствующих, человек лет сорока по имени Рональд Эйлмер Фишер, предложил развеять сомнения с помощью «передовой» методики — проведения эксперимента. Очевидно, что опыт нельзя было провести всего с двумя чашками, так как в этом случае вероятность угадывания равнялась 1/2. В этом случае нельзя определить, действительно ли участник эксперимента смог отличить по вкусу один напиток от другого или же попросту угадал. Однако если бы перед участником эксперимента стояло по 4 чашки с каждым напитком, вероятность угадывания равнялась бы всего 1 к 70 (так как существует 70 способов выбрать 4 чашки из 8). Если бы в этих условиях испытуемый смог точно определить, что было налито в каждую чашку сначала, чай или молоко, это означало бы, что способ приготовления чая действительно можно определить на вкус с небольшой, притом известной, погрешностью. Фишер в те годы уже был известным ученым. В 1935 году он опубликовал ставший классическим труд The Design of Experiments о стратегиях выбора экспериментальных данных. Во второй главе его книги некоторые ключевые понятия проиллюстрированы именно этим примером с чашками чая.Рассуждения дегустатора чая
Сначала предположим, что дегустатор чая не может различить, что было добавлено в чашку сначала, чай или молоко. Это предположение совершенно логично. Опровергнуть первоначальную гипотезу могут только результаты качественно продуманного и проведенного эксперимента. Исходная гипотеза будет опровергнута, если результаты эксперимента окажутся маловероятными при допущении, что дегустатор действительно не может различить чашки. Какие именно результаты окажутся «маловероятными», определяем мы сами: менее 5 % случаев, менее 1 % случаев или любое другое число. Допустим, мы готовы поверить, что дегустатор чая действительно может различать чашки, только тогда, когда вероятность случайного угадывания не будет превышать 5 %. Следовательно, эксперимент, в котором нужно выбрать 3 чашки из 6, будет некорректным, так как это можно сделать 20 различными способами, и вероятность случайного угадывания составит ровно 1 к 20, то есть 5 %. Это нетрудно проверить: первую чашку можно выбрать шестью способами, вторую — пятью, третью — четырьмя, следовательно, 3 чашки можно выбрать 6·5·4 = 120 способами. Однако здесь мы учитываем порядок выбора, то есть предполагаем, что чашки подписаны буквами от А до F и считаем варианты ADF и FDA различными. Чтобы учесть повторы, нужно поделить число вариантов на число способов, которыми можно упорядочить 3 чашки (3·2·1 = 6). Следовательно, выбрать 3 чашки из 6 можно 120/6 = 20 способами. Если нужно правильно выбрать 4 чашки из 8, то число вариантов будет равняться (8·7·6,5)/(4·3·21) = 70. Так как выбрать случайным образом все 4 чашки, в которых был сначала налит чай, а затем — молоко, можно только одним способом, то вероятность угадывания равняется 1 к 70, то есть 1,4 %. Если участник эксперимента верно укажет на 3 чашки из 4, это не будет доказывать, что вкус чая будет отличаться: вероятность правильного выбора трех чашек случайным образом равна примерно 23 %. Но не стоит тратить все силы на математические рассуждения. Также нужно уделить очень большое внимание деталям проведения эксперимента, отсутствию подсказок для испытуемого и другим нюансам. Фишер прямо указывает, что чашки в эксперименте должны располагаться случайным образом: «Наш эксперимент состоит в том, что мы приготовим восемь чашек чая с молоком, четыре — одним способом, четыре — другим, после чего подадим чашки, расположенные в произвольном порядке, дегустатору, который вынесет свой вердикт. Порядок проведения эксперимента объясняется дегустатору заранее: он должен попробовать чай из восьми чашек в произвольном порядке (определенном с помощью игральных костей, рулетки, карт или просто с помощью случайно выбранных чисел). Задача дегустатора — разделить чашки на две группы по четыре в зависимости от того, что было налито в каждую чашку сначала — чай или молоко». Каков же был результат эксперимента? Фишер не упоминает об этом в своей книге, но среди присутствующих находился профессор Хью Смит, который рассказал об этом случае Дэвиду Салсбергу, автору превосходной книги о бурном развитии статистики в XX веке. Книга называется The Lady Tasting Tea. В тексте подробно описывается этот эксперимент, который и дал название книге. По словам Хью Смита, леди действительно удалось точно указать все четыре чашки.

The Design of Experiments — классический труд, автор которого, Рональд Фишер, на примере дегустатора чая объясняет суть своего метода. * * *
РОНАЛЬД ЭЙЛМЕР ФИШЕР: В НУЖНОЕ ВРЕМЯ В НУЖНОМ МЕСТЕ Рональд Фишер родился в 1890 году. Он получил очень хорошее математическое образование и внес важный вклад в статистику и генетику. Хотя какого-либо официального рейтинга не существует, Рональд Фишер несомненно входит в число ученых, которые внесли наибольший вклад в развитие статистики в XX веке. Согласно некоторым источникам, он был болезненным ребенком, но отличался большой тягой к знаниям и очень интересовался астрономией. Также у него было очень плохое зрение, и врачи запретили ему читать при искусственном свете (не забывайте, что в те времена лампы отличались от современных). Это мешало ему заниматься, и чтобы Рональд не отставал от остальных, преподаватель обучал его математике, не используя ни бумаги, ни карандаша. Это способствовало развитию у Фишера великолепного геометрического мышления, что впоследствии позволило ему решать сложные задачи оригинальным геометрическим методом. В возрасте 29 лет он вместе с женой, которой в то время было 20 лет и которая родила ему троих детей (обычаи того времени отличались от современных), переехал на старую ферму около опытной сельскохозяйственной станции Ротамстед к северу от Лондона. Владельцы станции, производители удобрений, заключили с ним контракт, желая, чтобы Фишер помог им упорядочить огромный объем данных, накопленный за 90 лет работы станции. Ученый показал, что при использованном способе сбора данных влияние дождей и погоды в целом нивелировало возможный эффект от применяемых удобрений. Говорить о влиянии отдельных факторов на основе имеющихся данных было нельзя. Однако Фишер не просто указал, что данные собирались неверно, но и объяснил, какие поправки следует внести. Написанная им книга The Design of Experiments полностью изменила представление о способах сбора экспериментальных данных и оказала огромное влияние на исследования в сельском хозяйстве и промышленности.
* * *
Вес, рост, коэффициент корреляции и его значение
Мы знаем, что рост и вес человека связаны и что высокие люди обычно весят больше, чем низкие (разумеется, существуют исключения, но мы говорим об общем правиле). Здесь речь не идет о строгой связи: нет математической формулы, с помощью которой можно вычислить вес человека, зная его рост. Тем не менее существует тенденция, определенная взаимосвязь. На следующей диаграмме показана связь роста и веса в группе из 92 студентов университета (использовались данные, входящие в пакет статистических программ Minitab, о котором мы уже упоминали в главе 1).

Соотношение между весом и ростом в группе из 92 студентов.
Как вы охарактеризуете эту зависимость? Она «сильная», «заметная» или «слабая»? Как вы понимаете, в подобных ситуациях необходимо оценивать зависимость более точно. Для этого используется показатель, называемый коэффициент корреляции (иногда его называют коэффициентом корреляции Пирсона). Формула для вычисления коэффициента корреляции несколько громоздка, но вывести ее нетрудно (не беспокойтесь, мы не будем выводить эту формулу). По сравнению с другими похожими показателями коэффициент корреляции обладает многими преимуществами: его значения всегда лежат в интервале от —1 до 1 и не зависят от единицы измерения исходных данных. В нашем случае коэффициент корреляции не изменится, если мы будем использовать сантиметры и килограммы вместо дюймов и фунтов (как в исходных примерах). Если коэффициент корреляции равен 1, это означает, что между двумя переменными существует строгая зависимость. При увеличении значения одной переменной значение другой также увеличится. В этом случае между переменными действительно присутствует математическая зависимость, и зная значение одной переменной, можно точно вычислить значение другой. Однако в реальности подобная ситуация встречается крайне редко. Если коэффициент корреляции равен, например, 0,8, это означает наличие четкой взаимосвязи. В нашем примере коэффициент корреляции равен 0,785. Если он равен нулю, это указывает на отсутствие какой-либо взаимосвязи. Отрицательные значения означают то же, что и положительные, с единственной разницей: с ростом значения одной переменной значение другой будет не увеличиваться, а уменьшаться.

Расчет коэффициента корреляции с помощью Excel.
Однако этот показатель имеет свои недостатки (ничто не совершенно!). Если взаимосвязь между переменными отсутствует, не следует ожидать, что коэффициент корреляции будет равен нулю. Это будет означать, что данные распределены абсолютно равномерно, что не встречается на практике. Коэффициент корреляции может быть примерно равным нулю, но что именно означает это «примерно равен»? Кроме того, значение этого коэффициента зависит от объема исходных данных. Если объем исходных данных невелик, а значение коэффициента корреляции далеко от нуля, это не означает наличие корреляции. Если даны всего лишь два значения каждой переменной, то коэффициент корреляции всегда будет равен 1 или —1 вне зависимости от того, присутствует ли корреляция на самом деле. На следующей диаграмме представлено 35 точек, коэффициент корреляции равен 0,494. Это значение достаточно далеко от нуля, чтобы можно было говорить о присутствии корреляции? Или же это расположение точек можно получить случайным образом и переменные никак не связаны между собой?

Существует ли взаимосвязь между этими переменными?
Чтобы определить, действительно ли полученный коэффициент корреляции свидетельствует о взаимосвязи (или, если говорить на языке статистики, является ли это значение статистически значимым), используем моделирование. Сгенерируем два множества случайных чисел по 35 чисел в каждом. Очевидно, что эти числа будут никак не связаны между собой, однако коэффициент корреляции между ними не будет строго равен нулю, а будет равняться, например, — 0,123. Если мы заново сформируем эти два множества случайным образом и повторим моделирование 10000 раз, то получим 10000 значений коэффициента корреляции между двумя совокупностями из 35 чисел, которые никак не связаны между собой. Чтобы рассчитать эти значения, используем небольшую программу. Результат ее работы представлен на следующей гистограмме. Вертикальной чертой обозначено значение коэффициента корреляции, полученное нами в предыдущем примере, равное 0,494.

Значения коэффициента корреляции для двух совокупностей из 35 не связанных между собой чисел.
Из гистограммы следует, что коэффициент корреляции действительно может принять полученное значение, если переменные не связаны между собой, но очевидно, что вероятность этого крайне мала. Анализ результатов моделирования показывает (на гистограмме это не заметно), что 12 значений больше 0,494, 9 — меньше —0,494. Это означает, что полученное нами значение (или большее) выпадает примерно два раза из 1000, если исходные переменные независимы. Может ли быть так, что наш случай — именно тот, что выпадает два раза из 1000? Это неизвестно, но маловероятно. Разумнее всего полагать, что проанализированные нами переменные, соответствующие весу и росту 35 женщин в группе из 92 студентов, взаимосвязаны.
Схема рассуждений: проверка статистических гипотез
И в задаче, поставленной перед дегустатором чая, и в задаче о связи между переменными, которую мы только что рассмотрели, нужно ответить, по сути, на один и тот же вопрос: разумно ли считать, что дегустатор может различить вкус чая, приготовленного по-разному? Можно ли считать, что две переменные коррелируют? В обоих случаях, чтобы ответить на этот вопрос, нужно действовать по одной и той же схеме. 1. Нужно сформулировать исходную гипотезу. Чаще выбирается консервативная гипотеза: в задаче о дегустаторе чая мы предполагаем, что он не способен различить чай на вкус, а в задаче о корреляции — что переменные никак не связаны. 2. На основе доступных данных рассчитывается требуемая величина. Если данные отсутствуют или использовать их нельзя, нужно получить подходящие данные. В задаче о связи между переменными искомой величиной является коэффициент корреляции. В задаче о дегустаторе чая искомой величиной является число неверно указанных чашек во время эксперимента. 3. Если полученное значение находится в интервале, соответствующем исходной гипотезе, нет никаких оснований полагать, что исходная гипотеза ошибочна. Следовательно, мы будем по-прежнему ее придерживаться. Если полученное значение маловероятно, мы заменяем исходную гипотезу альтернативной (дегустатор может различить чай на вкус, переменные взаимосвязаны). В учебниках по статистике исходная гипотеза называется нулевой гипотезой, альтернативная (верная в случае, когда исходная гипотеза не выполняется) совершенно ожидаемо называется альтернативной гипотезой. Вероятность, с которой может быть достигнуто полученное значение статистического показателя (при условии, что нулевая гипотеза верна), называется р-значение. Этому числу уделяется особое внимание в статистических исследованиях, так как именно оно указывает, следует ли придерживаться нулевой гипотезы или будет разумнее отказаться от нее. В нашем случае, если дегустатор чая правильно указывает 4 чашки из 4, мы можем отвергнуть нулевую гипотезу с р-значением, равным 1,4 %. В задаче о взаимосвязи двух переменных р-значение равно 2 %: если бы переменные не были бы взаимосвязаны (нулевая гипотеза верна), то вероятность того, что коэффициент корреляции был бы равен или больше полученного нами, равнялась бы 2 %.
Что, если нулевую гипотезу нельзя опровергнуть? Если р-значение велико, то нельзя сказать, что результат противоречит нулевой гипотезе. Однако это совершенно не означает, что мы доказали истинность этой гипотезы. Именно поэтому говорят о том, что нулевая гипотеза отвергается (либо нет), а не принимается, и тем более не говорят о доказательстве истинности нулевой гипотезы. Обычно проводят такую аналогию: как известно, нулевая гипотеза суда заключается в том, что обвиняемый невиновен. Иными словами, он считается невиновным, если не найдено доказательств его вины. Собранные улики являются доказательствами, которые подтверждают или опровергают нулевую гипотезу. Если на одежде обвиняемого были найдены пятна крови жертвы, это очевидно свидетельствует не в пользу гипотезы о его невиновности. Однако если пятен нет, то это может означать, что преступление было тщательно спланировано или же полиция действовала неудачно, следовательно, обвиняемого нельзя осудить (то есть отвергнуть нулевую гипотезу нельзя). Но это не доказывает, что подсудимый невиновен. * * *
НЕОБЫЧНЫЙ СЛУЧАЙ: РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ДЛЯ ТРЕХ ТОЧЕК Рональд Фишер первым получил общую формулу распределения для коэффициента корреляции. Он использовал столь нетривиальные математические методы, что Карл Пирсон, еще один ведущий статистик и редактор важнейшего научного журнала своего времени, по-видимому, не понял доказательства Фишера и препятствовал его публикации. Это, разумеется, не понравилось Фишеру. Инцидент положил начало вражде между двумя несомненно величайшими статистиками своего времени. Собственно, это совершенно не удивительно. Следствия формулы Фишера достаточно необычны. Если даны три точки, соответствующие значениям независимых переменных, то диаграмма распределения возможных значений коэффициента корреляции имеет необычную форму, прямо противоположную привычному колоколу Гаусса. Наиболее вероятные значения располагаются не в середине интервала, а на его концах.

Теоретическое распределение коэффициента корреляции между независимыми переменными для трех точек в соответствии с формулой, выведенной Фишером (слева), и результат моделирования, выполненного 10 000 раз (справа).
Если даны четыре точки, то все значения коэффициента корреляции равновероятны. Если дано пять точек, то наиболее вероятным значением является ноль. По мере роста числа точек начинает вырисовываться традиционный график в форме колокола.* * *
Еще один пример: сбалансированы ли игральные кости?
В главе 2 упоминается, что в 1850 году швейцарский астроном бросил пару игральных костей (красного и белого цвета) 20000 раз. Полученные результаты были достаточно далеки от ожидаемых теоретических значений. Это дает основания подозревать, что в эксперименте, возможно, использовались несбалансированные игральные кости. Так как все шесть возможных результатов являются равновероятными, если мы бросим игральные кости 20 000 раз, то теоретически каждое значение выпадет 20000/6 = 3333 раза. В следующей таблице представлены результаты эксперимента, теоретические значения и абсолютная величина отклонения от теоретических значений.

Являются ли эти отклонения достаточно большими, чтобы говорить о несбалансированности игральных костей? Или же эти отклонения могут возникнуть случайным образом? В конце концов, если бы результаты эксперимента в точности совпадали бы с теоретическими значениями, это тожевыглядело бы странно. Чтобы развеять сомнения, проверим статистическую гипотезу по той же схеме, что использовал Фишер для решения задачи о дегустаторе чая. Будем предполагать, что игральные кости сбалансированы, и отвергнем эту гипотезу только в том случае, если полученные данные будут явно ей противоречить. Будем анализировать максимальное отклонение между полученными и теоретическими значениями. В предыдущей таблице показано, что для красного кубика эта величина равна 417, для белого — 599. Зададимся вопросом: каковы ожидаемые значения этой величины для идеально сбалансированных игральных костей? И снова на этот вопрос можно ответить с помощью моделирования. Смоделируем 20000 бросков игральной кости, подсчитаем, сколько раз выпадет каждое значение, и рассчитаем максимальное отклонение от теоретического значения. При первом моделировании максимальное отклонение равнялось 83, при втором — 97. После того как моделирование было выполнено 10000 раз, была получена гистограмма, представленная на следующем рисунке. На ней также указаны значения, соответствующие красному и белому игральному кубику.

Распределение максимального отклонения для сбалансированных игральных костей и значения, полученные экспериментально.
Очевидно, что данные эксперимента противоречат гипотезе о сбалансированности игральных костей. Если бы эта гипотеза была верна, то вероятность получить подобные данные была бы очень, очень мала. В этом случае р-значение равно нулю с точностью до нескольких знаков после запятой. Следовательно, мы можем утверждать, что игральные кости несбалансированны, а вероятность того, что мы ошибаемся, практически равна нулю. В качестве показателя, обобщающего данные эксперимента, можно использовать не максимальное отклонение, а величину, в которой учитывается отклонение для всех шести возможных результатов броска игральной кости. Такой величиной может быть сумма всех отклонений, равных разности фактической и теоретической частоты, возведенных в квадрат (чтобы положительные и отрицательные отклонения не скомпенсировали друг друга), разделенная на теоретическую частоту. Для красной игральной кости эта величина будет равна

Расчеты могут показаться вам излишне сложными, но эта величина обладает определенным преимуществом: она не требует моделирования распределения для случая, когда нулевая гипотеза верна (так называемого эталонного распределения). Эта величина называется критерий х2 (хи-квадрат). Ее впервые использовал в 1900 году Карл Пирсон, сыгравший важную роль в истории статистики. Мы уже упоминали его имя, когда говорили о коэффициенте корреляции. Для обычных статистических тестов нет необходимости в моделировании распределения величины. Вместо этого оно выводится с помощью математических методов. Формула для расчета распределения коэффициента корреляции достаточно сложна и не имеет своего названия, хотя при большом размере выборки это распределение близко к нормальному. Первым, кто вывел формулу для этого распределения, был не кто иной, как Рональд Эйлмер Фишер. * * *
СЛИШКОМ МАЛОЕ ОТКЛОНЕНИЕ ТОЖЕ ПОДОЗРИТЕЛЬНО Если мы бросим идеально сбалансированную игральную кость 20000 раз, то каждое из возможных значений выпадет примерно 20 000/6 = 3333 раза. Отклонение фактической и теоретической частоты редко превышает 250. Это происходит всего один раз на каждые 100000 симуляций. Однако также весьма необычно, если фактические значения очень близки к теоретическим. Допустим, игральная кость была брошена 20000 раз и были получены следующие результаты:

Есть основания подозревать, что эта информация недостоверна, так как столь малое отклонение фактической и теоретической частоты встречается всего один раз на миллион. Фишер обнаружил любопытное совпадение между экспериментальными данными, опубликованными Менделем в его знаменитых работах о наследственности, и ожидаемыми теоретическими значениями. Удивительнее всего то, что Мендель ошибочно спрогнозировал результаты некоторых экспериментов, но полученные данные тем не менее были подозрительно близки к прогнозным значениям. По мнению Фишера, данные скорректировал необязательно сам Мендель, а кто-то из его ассистентов, который недобросовестно отнесся к работе и решил подменить реальные данные именно теми, которые ожидал увидеть Мендель. Этот вопрос спровоцировал бурное обсуждение. Эта задача относится не только к теории вероятности, но также к генетике и ботанике, так как в ней идет речь о фундаментальном механизме наследования признаков у растений. Споры не утихали длительное время, но какой-то определенный итог этих дискуссий подвести трудно. Стороны сходятся на том, что нет четких доказательств того, что Мендель или кто-то еще скорректировал результаты эксперимента.* * *
До сих пор это верно, далее — нет: границы р-значения
Как правило, выбирается определенное p-значение, чаще всего 5 %, и если полученное на практике p-значение оказалось меньше, то нулевая гипотеза отвергается, в противном случае — нет. Это значение называется уровнем значимости. Конечно, всем нам нравятся четкие и простые правила, но было бы неразумно выбрать одно универсальное значение и применять его всегда вне зависимости от контекста. Выбор граничного значения равносилен выбору вероятности того, что мы ошибочно отвергнем нулевую гипотезу. Вероятность ошибки, которую будет разумно выбрать, зависит от ситуации и возможных последствий ошибки. Предположим, как-то утром, выходя из дома, мы смотрим прогноз погоды и решаем, что вероятность дождя равна 10 %. Стоит ли взять с собой зонтик? Если мы не возьмем с собой зонтик и примем 10-процентный риск попасть под дождь, никому из нас это не покажется неразумным. Если мы ошибемся, то потеряем немного (разве что слегка намокнем). Также следует учесть, что ходить весь день с зонтиком достаточно неудобно. Другой пример. Мы едем по второстепенной дороге, на которой очень мало машин. Мы замечаем, что на подъеме, где не видно встречную полосу, есть небольшая выбоина. Ее можно объехать, приняв немного левее. Однако мы не станем этого делать. Вероятность того, что по встречной полосе этой пустынной дороги проедет автомобиль, невелика, а вероятность того, что мы встретимся точно на подъеме, — еще меньше. Однако мы не станем выезжать на встречную полосу: несмотря на то что вероятность столкновения крайне мала, если оно все же произойдет, то ущерб будет значительным. Если мы проедем по выбоине, то почувствуем лишь легкое неудобство. Очевидно, что вероятность ошибки, к которой мы готовы при принятии решения, зависит от обстоятельств и от возможных последствий этой ошибки. Приведем другой пример, также связанный с дорожным движением, а именно с радарами для измерения скорости проезжающих машин. Хорошо известно, что эти радары, как и любые другие приборы, имеют определенную погрешность измерения. Если они показывают, что скорость машины равна 120 км/ч, возможно, что фактическая скорость равна 119 или 122 км/ч. По этой причине, если на дороге установлено ограничение скорости в 120 км/ч, водителей штрафуют только тогда, когда их скорость превышает ограничение на определенную величину. Это делается для того, чтобы исключить возможное влияние погрешности измерения и гарантировать, что водитель действительно ехал с превышением. Если будет выбрано значение, для которого доля ошибочных значений будет равна 5 % (таким образом, в 5 % случаев будут оштрафованы водители, которые не превышали скорость), это вызовет жаркие споры, ведь каждый день сотни людей будут незаслуженно получать штрафы. Подведем итог. Выбор граничного значения нельзя делать только с помощью методов статистики; нужно рассматривать конкретную ситуацию. Когда проводится эксперимент, в котором сравнивается эффективность нового и существующего лекарств, выбор граничного значения 0,05 означает, что с вероятностью в 5 % будет сделан ошибочный вывод об эффективности лекарства. Какие последствия это повлечет? Имеет ли новое лекарство серьезные побочные эффекты? Дороже ли новое лекарство, чем то, что уже используется? Ответы на эти вопросы крайне важны при выборе оптимального граничного значения. Однако верно и то, что во многих случаях значение 0,05 выбирается без какого-либо анализа. Это происходит потому, что для этого значения уже рассчитаны различные статистические показатели, которые можно найти в справочных таблицах. Когда много лет назад эти величины рассчитывались с помощью примитивных средств, в таблицы заносились лишь значения, соответствующие определенным вероятностям, в частности 0,001; 0,005; 0,01; 0,05; 0,10. Из возможных табличных значений в качестве границы, отделяющей «обычное» от «необычного», чаще всего выбиралось именно 0,05. Преимущество этого значения в том, что это круглое число в нашей десятичной системе счисления. Если бы у нас на руках было по шесть пальцев, то в качестве граничного значения было бы естественно выбрать 0,06.
Глава 5 Что лучше? Что эффективнее? Как формировать выборки для ответов на подобные вопросы
Статистику необходимо использовать тогда, когда для ответа на вопрос нужно собрать и проанализировать данные. К таким вопросам относятся, например, вопросы об эффективности вакцины или лекарства, о прочности нового способа сварки и другие. Как правило, сбор данных — трудоемкая и дорогостоящая операция. Следует тщательно продумать, каков оптимальный способ решения этой задачи, позволяющий потратить минимум ресурсов. Кроме того, почти никогда не удается получить все необходимые данные и нужно знать, как извлечь из них максимальную выгоду. Не стоит забывать и о вариации данных, которые не подчиняются строгим математическим законам, и при одних и тех же исходных данных результаты могут различаться. Если нужно ответить на вопрос, снижает ли регулярный прием определенной дозы аспирина вероятность инфаркта, это можно сделать на основе рассуждений о действии аспирина на организм, однако во многих случаях реальность преподносит немало сюрпризов. Точнее всего на этот вопрос можно ответить, если собрать экспериментальные данные. Нужно сформировать две группы людей, обладающих как можно более схожими признаками, одной группе прописать аспирин, другой — нет, после чего сравнить результаты. Нам известно, что не все участники исследования одинаковы, поэтому реакция на аспирин у них будет различаться. Нужно учесть все эти факторы и сделать корректные выводы, указав степень их надежности. Именно этим и занимается статистика.Крупномасштабное исследование: вакцина против полиомиелита
Возможность сделать прививку и обезопасить себя от инфекционного заболевания, вне всяких сомнений, стала одним из решающих этапов в борьбе с болезнями, помогла улучшить здоровье людей и повысить ожидаемую продолжительность жизни. Однако для каждого заболевания требуется особая вакцина, и найти ее иногда бывает непросто. Лабораторные тесты, тесты на животных, на добровольцах помогают собрать достаточно информации об эффективности вакцины. Однако прежде чем одобрить и рекомендовать ее к массовому применению, нужно тщательно проверить, скомпенсируют ли ее преимущества затраты и неизбежные риски. Здесь на сцену выходит статистика. В 1954 году было проведено масштабное исследование по оценке эффективности вакцины против полиомиелита (вакцины Солка, созданной эпидемиологом Джонасом Солком). Оно очень подробно описано в книге Statistics: A Guide to the Unknown, где рассказывается о 29 случаях применения статистики в самых разных областях. Каждая глава написана специалистом, глубоко разбирающимся в соответствующей теме. Глава об анализе эффективности вакцины написана профессором Чикагского университета Полом Мейером.
Полиомиелит и его особенности Благодаря эффективности прививок полиомиелит исчез практически полностью, но еще не так давно он входил в число самых опасных болезней. Им болели преимущественно дети, многие оставались парализованы или всю жизнь страдали от серьезных осложнений болезни. Кроме того, масштабные эпидемии полиомиелита возникали неожиданно. Что любопытно, от них в большей степени страдали социальные группы с лучшими условиями жизни, а наиболее бедные страны и слои населения оказывались практически не затронутыми. Причиной этому был тот факт, что в менее благополучных слоях населения дети заражались раньше, когда они еще находились под защитой иммунитета матери, поэтому вирус не приводил к развитию заболевания. Кроме того, у детей вырабатывался иммунитет к полиомиелиту. Дети, жившие в более благоприятных условиях, заболевали позже, когда их уже не защищал материнский иммунитет. Борьбе с этой болезнью способствовал и тот факт, что сам президент Рузвельт переболел полиомиелитом и всячески поддерживал исследования в этой области. В начале 1950-х годов руководство системы здравоохранения США посчитало, что новая вакцина, созданная Джонасом Солком, является эффективной, что было доказано исследованиями, проведенными в небольших масштабах. Однако перед тем как рекомендовать массовое применение вакцины, требовалось получить неопровержимые доказательства ее эффективности и отсутствия негативных побочных эффектов. Было решено провести эксперимент, ставший самым крупным в истории системы здравоохранения.
Контрольная группа Допустим, что результаты испытаний нового лекарства от определенной болезни показывают, что любой, кто принял это лекарство, излечивается за 7 дней. Можно ли говорить об эффективности этого лекарства? Возможно, вам кажется, что если все заболевшие излечиваются, то лекарство и в самом деле эффективно. Однако на самом деле эксперимент не доказывает этого. Возможно, что если бы испытуемые не принимали никакого лекарства, то излечились бы за тот же срок. Более того, возможно, что без принятия лекарства болезнь проходит за 2–3 дня, в противном случае на ее лечение уходит 5–6 дней. По этой причине для доказательства эффективности нового лекарства или вакцины формируется репрезентативная выборка из числа тех, кому предназначено лекарство. Затем выборка разделяется на две группы случайным образом. Это обеспечивает отсутствие системных различий между представителями той и другой группы. Далее лекарство получают пациенты лишь из одной группы. Путем сравнения с пациентами второй группы анализируется эффект от нового лекарства. Группа, которая не получает никакого лечения, называется контрольной группой. В случае с полиомиелитом регулярно отмечались непредсказуемые колебания числа заболевших. Например, в 1952 году, когда произошла наиболее серьезная вспышка полиомиелита за период с 1930 по 1956 год, в США заболело порядка 60000 человек; в 1953-м — всего лишь около 35000, на 42 % меньше. Если бы в 1953 году была испытана новая, абсолютно неэффективная вакцина, можно было бы предположить, что она эффективна, так как число заболевших существенно снизилось. Этот случай был не единственным: в 1932 году по сравнению с предыдущим годом число заболевших уменьшилось более чем наполовину. Это же произошло в 1936, 1938, 1942, 1947 и 1956 годах. Столь же неудачной была бы попытка привить всех детей в одном регионе, например в штате Нью-Йорк, и не привить детей, например, в Чикаго, так как болезнь распространялась неравномерно и крупная вспышка заболевания могла произойти в конкретном штате именно в этом году. Было необходимо разделить всех испытуемых на две равные группы, находящиеся в абсолютно равных условиях. Одной группе вводилась бы вакцина, вторая группа являлась бы контрольной.
Две «наиболее похожие» группы: плацебо и двойной слепой метод Если некоторые люди получают лекарство (принимают ежедневно по одной таблетке или получают разовый укол, как в случае с вакциной Солка), а другие не получают ничего, то первые будут убеждены, что лекарство имеет определенный эффект, и отметят некоторое улучшение, даже если лекарство не будет обладать никаким эффектом. Этот феномен называется эффектом плацебо. Несомненно, именно он является причиной успеха многих видов так называемой альтернативной медицины, когда заболевание проходит как бы само собой. В случае с полиомиелитом ребенок либо подвержен заболеванию, либо нет, и можно подумать, что ощущения пациента не будут зависеть от того, получил он прививку или нет. Однако не все варианты течения болезни являются тяжелыми или имеют осложнения. Если у ребенка, получившего прививку, обнаруживаются симптомы, сходные с симптомами полиомиелита, то и родители, и врач посчитают, что ребенок вряд ли мог заразиться, ведь он получил прививку! То есть если у ребенка действительно была легкая форма полиомиелита, ее можно перепутать с другой болезнью, и этот случай заболевания окажется незарегистрированным. Напротив, члены группы, не получившей вакцину, будут обращать больше внимания на любые симптомы, так как будут чувствовать себя незащищенными. Если у них обнаружатся признаки заболевания, эти случаи будут изучены и диагностированы более тщательно. В результате может возникнуть ошибочное представление о том, что в группе, не получившей прививок, отмечено больше случаев болезни. Чтобы избежать положительного воздействия эффекта плацебо только на группу, получавшую лечение, все испытуемые получают внешне одинаковое лекарство. Они не знают, принимают они настоящее лекарство или им дают нейтральные таблетки того же вкуса и цвета, что и настоящие, — эти таблетки и называются плацебо. Более того, сам испытуемый не знает, к какой группе он принадлежит (в случае с полиомиелитом нужно, чтобы об этом не знал ни ребенок, ни его родители), а врач, который проводит лечение, не знает, какое лекарство принимает пациент — настоящее или плацебо. Это делается не потому, что врачам нельзя доверять, а для того чтобы избавиться от возможных стереотипов. Так, если ребенок получает настоящее лекарство и врач замечает признаки улучшения, он несколько преувеличит их, а если врачу известно, что ребенок получает плацебо, то он будет больше обращать внимание на отрицательные, а не на положительные симптомы. * * *
ЗНАЧИМЫЕ И ВАЖНЫЕ РАЗЛИЧИЯ При сравнительном анализе самое главное — определить, являются ли наблюдаемые различия значимыми или нет. Именно в этом заключается цель всех статистических тестов. Может показаться, что это противоречит здравому смыслу, но если различия являются значимыми, то это не означает, что они важные. Различия называются значимыми, когда считается, что они не являются случайными, и два рассматриваемых способа лечения действительно дают разные результаты. Однако мы можем быть уверены, что они действительно дают разные результаты, даже если эта разница будет незаметна на практике. Например, эксперимент может показать, что один клей приклеивает лучше другого, но разница между ними практически незаметна. Может случиться, что из-за недостаточного объема данных или значительной вариации результатов различия будут очень большими, но при этом они будут вызваны случайными факторами. Иными словами, в таком случае нельзя сказать, что один клей действительно лучше другого.* * * Чтобы этого не произошло, подобные исследования проводятся так, чтобы ни пациент, ни врач не знали, кто принимает настоящее лекарство, а кто — плацебо. Именно поэтому этот метод называется двойным слепым методом. Однако и при формировании контрольной группы, получающей плацебо, также присутствуют определенные трудности. Одна из их — сложность организации эксперимента. В случае с вакциной Солка требовалось приготовить инъекции с вакциной, идентичные тем, что содержали только соляной раствор. Далее их нужно было пронумеровать и проконтролировать, инъекцию какого типа получает пациент. При этом ни персонал, вводивший инъекцию, ни лечащий врач не должны были знать, какой именно препарат вводится пациенту. Еще одна проблема лежит в области этики. Некоторые полагали, что неразумно вводить детям соляной раствор вместо вакцины, которая, как считалось, была достаточно эффективной. В качестве альтернативы было предложено вводить вакцину детям, которые учились во втором классе, а учеников первого и третьего класса использовать в качестве контрольной группы. В этом случае нарушался основной принцип двойного слепого метода, однако примерно в половине штатов, где проводился эксперимент, был использован именно этот способ. В остальных штатах контрольные группы получали плацебо.
Необходимость в выборке очень большого размера Доля заболевших составляла всего 50 человек на 100 000. Ожидалось, что применение вакцины позволит сократить число заболевших вдвое. Очевидно, что проведение экспериментов с малыми группами было невозможным. Если бы, например, мы ввели вакцину 1000 детей, а еще 1000 использовали в качестве контрольной группы, то, скорее всего, ни в одной группе не было бы ни одного заболевшего и эксперимент не имел бы смысла. Если бы численность каждой группы составляла 10 000 человек, могло случиться так, что в контрольной группе заболели 5 человек, в группе получивших вакцину — 2 человека. Эта разница столь мала, что ее можно назвать случайной (отвергнуть нулевую гипотезу о том, что доля заболевших в каждой группе одинакова, в этом случае нельзя). Было необходимо, чтобы численность групп составляла несколько сотен тысяч человек, чтобы результаты можно было считать достоверными. Требовался крупномасштабный эксперимент.
Результаты Эффективность вакцины полностью подтвердилась. В вакцинированной группе число заболевших было в два с лишним раза меньше, чем в группе, которой вводилось плацебо. Использованное в эксперименте p-значение имело порядок 10-9. Иными словами, вероятность того, что число заболевших в обеих группах случайно оказалось бы одинаковым, равнялась 1 на миллиард.

Результаты в тех регионах, где в качестве контрольных групп использовались школьники старших и младших классов, оказались аналогичными. Все были довольны тем, как был проведен эксперимент, ведь результаты оказались даже лучше, чем ожидалось. Число заболевших среди вакцинированных оказалось заметно меньше, но если бы в эксперименте не использовалась контрольная группа, которой вводилось плацебо, эксперимент не помог бы окончательно развеять все сомнения, а его результаты можно было бы трактовать по-разному.
Роль статистики. Полиомиелит в наши дни Вакцина Солка позволила совершить шаг вперед в борьбе с полиомиелитом, но результаты ее использования все еще были не вполне удовлетворительны, и через несколько лет на смену ей пришла другая, более эффективная вакцина. Перед началом массового применения были должным образом проведены необходимые статистические исследования. Сегодня полиомиелит практически исчез. В настоящее время вспышки полиомиелита отмечаются всего в четырех странах мира: Нигерии, Индии, Пакистане и Афганистане. Всемирная организация здравоохранения, ЮНИСЕФ и другие международные организации предпринимают усилия по борьбе с полиомиелитом в этих странах. По их оценкам, очень скоро перестанут отмечаться новые случаи этого заболевания. Через три года после того, как это произойдет, будет официально объявлено об исчезновении полиомиелита.
Аспирин и инфаркты
В 1983 году в США было проведено крупномасштабное исследование для оценки влияния аспирина на сердечно-сосудистые заболевания. Анализ малых групп показал, что прием аспирина может снизить вероятность повторного сердечного приступа. Однако не было никаких доказательств того, что этот положительный эффект аспирина распространяется на всех. Для участия в эксперименте было приглашено 261 248 врачей мужского пола старше 40 лет, данные о которых были взяты из реестра Американской медицинской ассоциации. 59 285 человек выразили согласие участвовать в эксперименте. Из их числа следовало исключить людей со сложной историей болезни, тех, кто уже принимал аспирин, а также тех, у кого наблюдались побочные эффекты от аспирина. В итоге был отобран 22 071 врач. Все они были здоровы и не находились в группе риска. Им было предписано принимать по 325 мг аспирина (или плацебо) раз в два дня. Одновременно с исследованием влияния аспирина был изучен эффект бета-каротина (химического соединения, которое в нашем организме преобразуется в витамин А) при определенных типах рака. Испытуемые были случайным образом разделены на четыре группы: члены первой группы принимали аспирин и бета-каротин, второй группы — аспирин и плацебо бета-каротина, третьей группы — плацебо аспирина и бета-каротин, четвертой группы — плацебо аспирина и плацебо бета-каротина.

Лекарства, которые принимали четыре группы участников эксперимента. Все таблетки выглядели одинаково. Звездочкой отмечены таблетки-плацебо.
Несмотря на строгие критерии отбора участников эксперимента, они отличались по возрасту, истории болезни, характеру, некоторые из них курили. Следовательно, требовалось очень внимательно разделить участников эксперимента на четыре группы случайным образом, так как только таким способом можно было гарантировать общую схожесть групп по составу. Можно возразить, что большинство людей, находившихся в предынфарктном состоянии, случайным образом попали в одну из групп. Однако, согласно теории вероятности, если распределение проводилось действительно случайным образом, то вероятность подобного исхода в большой группе ничтожна. Так как состав всех четыре групп схож и все испытуемые находились под влиянием одинаковых внешних условий, существенные различия в результатах групп, выходящие за рамки случайного отклонения, объясняются только разным действием принимаемых лекарств. Именно такова логика экспериментов, в которых сравнивается действие различных лекарств на случайной выборке. Использовался двойной слепой метод, то есть ни пациенты, ни лица, наблюдающие за ними, не знали, какое лекарство принимает тот или иной пациент. Наблюдательный комитет анализировал результаты каждые полгода. Хотя изначально планировалось, что эксперимент продлится семь лет, спустя пять лет после его начала он был прекращен: положительный эффект аспирина оказался столь существенным, что было принято решение как можно скорее оповестить об этом и участников эксперимента, и всех врачей страны.

В группу, получавшую аспирин, входили те, кто принимал аспирин и бета-каротин, а также те, кто принимал аспирин и плацебо бета-каротина. Группа плацебо включала две оставшиеся подгруппы. Статистическое исследование показывает, что если бы аспирин не имел никакого положительного эффекта (вероятность инфаркта в обеих группах была бы одинаковой), то вероятность того, что подобная разница в результатах случайна, имела бы порядок 2 на 100000. Следовательно, разумно предполагать, что аспирин снижает вероятность инфаркта. Новость о результатах эксперимента появилась на первой полосе газеты New York Times и привлекла большое внимание средств массовой информации. Эксперимент по анализу воздействия бета-каротина продолжался в течение запланированного времени. Автору не удалось найти информации о результатах этого эксперимента. Скорее всего, они были негативными. Согласно известной на данный момент информации, прием бета-каротина не только не снижает вероятность заболевания раком, но и увеличивает ее для курильщиков. Однако аспирин — тоже не панацея. Считается, что он препятствует образованию скоплений тромбоцитов и образуется меньше сгустков крови. Но это тоже таит в себе опасность. Исследования показали, что в группе, принимавшей аспирин, наблюдался небольшой (не статистически значимый) рост случаев смертности от эмболии. Поэтому решение о регулярном приеме аспирина следует принимать взвешенно. Нужно следовать рекомендациям врача, который оценит индивидуальные особенности, преимущества и недостатки приема аспирина в каждом конкретном случае.
Табак и рак легких
С тем, что курение вредит здоровью, сегодня согласны практически все, но эта точка зрения была распространена не всегда. Теперь нам известно, какие именно вещества, содержащиеся в табачном дыме, могут вызвать рак. Также известно, как эти вещества превращают здоровые клетки в раковые, — это было показано с помощью опытов на животных. Но, как и во многих других случаях, статистические данные указывали, что ситуация не столь однозначна и требуются более подробные исследования. Данные, которые были получены в 1950-х, свидетельствовали, что курильщики чаще болеют раком легких, чем некурящие. Но чтобы однозначно подтвердить это, требовались более тщательные исследования. Чтобы подтвердить связь между курением и возникновением рака легких и других заболеваний, было проведено семь масштабных исследований (одно в Великобритании, одно в Канаде, пять в США). Число испытуемых составляло от 34000 до 448000 человек. По сути, все исследования проводились по одной и той же схеме: лицам, выбранным для участия в исследовании, высылались анкеты. Требовалось указать, сколько сигарет человек выкуривал сейчас и в прошлом, а также основные демографические данные. Была создана система, гарантирующая, что в случае смерти участника опроса этот факт регистрировался, а также указывалась причина смерти. Эти исследования позволили узнать, какое влияние оказывает возраст, в котором человек начал курить, вид и число выкуриваемых сигарет, а также заболевания, которым подвержены те, кто бросил курить. Один из выводов исследования заключался в том, что частота заболевания раком легких среди курильщиков в 11–20 раз выше, чем среди некурящих. Возможен встречный аргумент (его выдвинул в том числе Фишер): данные исследований показывают, что раком легких чаще болеют курильщики, но это не доказывает, что причиной этого заболевания является именно табак. Можно предположить, что курильщики в целом более нервные и беспокойные, и именно эти черты характера, из-за которых они начали курить, являются причиной определенных заболеваний. Быть может, те, кто подвержен табачной зависимости, имеют определенную генетическую особенность, из-за которой (а не из-за курения) они чаще болеют раком легких. Эти аргументы можно выдвинуть потому, что проведенные исследования не являются экспериментами в полном смысле этого слова, как было в случае с испытаниями вакцины против полиомиелита или при изучении действия аспирина по профилактике сердечных заболеваний. В этих случаях участники эксперимента случайным образом делились на две группы, экспериментальную и контрольную, так чтобы все возможные различия между ними являлись следствием изучаемого явления. Считалось, что причиной любых существенных различий между двумя группами является именно изучаемое явление. Однако исследования воздействия табака не были экспериментальными: две группы, курильщики и некурящие, уже были сформированы, и ученые лишь наблюдали за развитием событий. Нельзя было заставить курить некурящих или уговорить заядлых курильщиков бросить курить. С теоретической точки зрения в идеальном исследовании курить должны все, но половина испытуемых, выбранная случайным образом, должна курить обычный табак, а другая половина — некое совершенно безвредное вещество, по вкусу и остальным свойствам идентичное табаку. Производители сигарет могли бы заявить, что только такое исследование является корректным, и были бы правы. Однако оно настолько же корректно, насколько и нереализуемо на практике. Все же доступные данные однозначно указывают, что табак — важный фактор возникновения рака легких и мочевого пузыря, сердечно-сосудистых и других заболеваний. Связь между раком легких и употреблением табака была отмечена во множестве исследований, выполненных в различных странах и условиях. Это устраняет возможную предрасположенность к этим заболеваниям определенной группы людей. Кроме того, известно, какие именно вещества, содержащиеся в табачном дыме, могут вызывать рак. Гипотеза о генетической предрасположенности не объясняет роста числа заболеваний среди женщин, которые начали курить, и среди некурящих, постоянно находящихся рядом с курильщиками. Эти факты не всегда были очевидны, и обнаружить их помогла именно статистика.
Случайный отбор и влияние различных факторов
При разработке экспериментов для сравнения различных лекарств, катализаторов химической реакции и так далее наиболее важный момент — получить два множества данных, которые отличаются единственной переменной, изучаемой в эксперименте. При проведении подобных экспериментов в медицине могут сравниваться два лекарства или выясняться эффект от приема лекарства по сравнению с плацебо, как в случае с вакциной полиомиелита или при анализе действия аспирина по предотвращению инфарктов. Как вы уже видели, ключевой вопрос — как разделить участников исследования на две максимально похожие группы. Парадоксально, но наилучшие результаты достигаются при формировании групп случайным образом. В этом случае любые значимые различия между группами (то есть те, которые нельзя объяснить случайными событиями) объясняются различным воздействием изучаемого фактора на обе группы. Однако если помимо изучаемого фактора на группы действуют и другие факторы, то нельзя сказать, что именно является причиной различий в результатах групп. Рассмотрим пример. Одной из классических книг по проведению экспериментов является Statistics for Experimenters Бокса, Хантера и Хантера, где объясняется, как нужно провести эксперимент, чтобы сравнить степень износа различных материалов, из которых изготавливается подошва молодежной обуви. Если в эксперименте участвует всего 10 молодых людей, их можно разделить случайным образом на две группы по 5 человек: члены одной группы получат обувь с подошвой из материала А, члены второй группы — обувь с подошвой из материала В. По прошествии определенного времени (например, полугода) нужно измерить износ подошв на всех парах обуви и провести соответствующий статистический анализ (в этом случае будет использоваться так называемый t-критерий Стьюдента для независимой выборки). Естественно, что группы следует формировать случайным образом. Не стоит просить подростков выстроиться в шеренгу и выдавать первым пяти обувь с подошвой из материала А, последним пяти — обувь с подошвой из материала В: те, кто встал в шеренгу первыми, больше бегают и двигаются, поэтому быстрее износят обувь. Однако этот способ сбора данных имеет один недостаток. Износ подошвы зависит не только от материала (именно это мы анализируем в ходе эксперимента), но и от самого подростка: некоторые из них больше бегают и будут даже играть в футбол в этой обуви, другие будут бегать меньше. Некоторые, возможно, почти не будут надевать выданную обувь, так как она им не понравится или они побоятся порвать ее, и подошвы не износятся. Так как на износ подошвы влияет не только материал, из которого она изготовлена, но и другие факторы, то мы не сможем определить, какой именно фактор будет причиной возможных различий. Может случиться так, что по вине посторонних факторов различий наблюдаться не будет, но в действительности подошвы из анализируемых материалов будут изнашиваться по-разному. Как справиться с этой проблемой? Нужно выдать каждому подростку один ботинок с подошвой из первого материала, другой — с подошвой из другого материала. В этом случае все возможные отличия в износе подошвы будут вызваны исключительно различными свойствами материалов и никаким другим фактором. В этом случае сравниваются не средние значения в обеих группах, а износ подошв обоих ботинок каждого подростка. Если одна подошва в среднем изнашивается больше другой (не имеет значения, насколько сильно они изнашиваются, важна лишь разница между ними), это вызвано различием в свойствах материалов. Для сравнения средних значений выборок, сформированных таким образом, используется так называемый t-критерий Стьюдента для парных выборок. Очевидно, что не следует изготавливать из материала А подошву только правых ботинок, а из материала В — подошву левых ботинок, так как, возможно, подошвы на одной ноге в среднем изнашиваются больше. Этого можно избежать, если чередовать материалы случайным образом (например, бросать монету для каждой пары обуви, и если выпадает решка, то из материала А изготавливается подошва правого ботинка). Таким образом, ожидается, что если обувь на конкретной ноге изнашивается больше, при чередовании материалов случайным образом возможное влияние этого фактора будет устранено. * * *
УИЛЬЯМ СИЛИ ГОССЕТ, ОН ЖЕ «СТЬЮДЕНТ» Любой, кто хотя бы немного изучал статистику, непременно сталкивался с распределением Стьюдента, которое используется даже чаще, чем нормальное распределение, или с t-критерием Стьюдента для сравнения средних значений. Стьюдент — это псевдоним, которым подписывал свои работы Уильям Сили Госсет (1876–1937), внесший огромный вклад в статистику. Всю свою жизнь он проработал на пивоваренном заводе Guinness в Дублине. В начале XX века, когда Госсет окончил курсы математики и химии в Университете Оксфорда, компания Guinness перешла в руки юного наследника, который решил отойти от традиционных способов изготовления пива и воспользоваться помощью ученых в разработке новых, более совершенных способов пивоварения. Одним из тех, кто был принят на работу, был Стьюдент. Он быстро понял, как важно использовать методы статистики при сравнении различных рецептов приготовления пива. Было необходимо изучить влияние сырья, характеристики которого существенно варьировались и были подвержены воздействию факторов окружающей среды. Требовалось проводить эксперименты, но их число всегда было недостаточным, и нужно было делать выводы на основе небольшого объема доступных данных. До того времени считалось, что использованные выборки всегда были достаточно велики, чтобы по ним можно было точно оценить параметры генеральной совокупности. Однако при работе с малыми выборками оценки были неточными, и ими нельзя было руководствоваться. Госсет занялся поисками решения этой задачи и опубликовал свои выводы под псевдонимом Стьюдент, поскольку сотрудникам компании запрещалось публиковать статьи с результатами своих исследований. Существует несколько версий того, как и почему Госсет выбрал себе такой псевдоним. По одной из версий, в компании Guinness стало известно об увлечении Госсета математикой уже после его смерти, однако другие источники указывают, что в компании знали о том, что он публикует статьи, а псевдоним Стьюдент предложил сам директор. По-видимому, целью Госсета было не сохранить в секрете разрабатываемые им теории, а скрыть от конкурентов, что Guinness использует статистические методы для улучшения качества продукции.

* * * Выбор материала случайным образом не ведет к дополнительным затратам и позволяет исключить влияние прочих известных и даже неизвестных факторов. Похожим примером является анализ износа различных видов покрытия, которое наносится на стекла очков. Если одной группе людей раздать очки с одним покрытием, другой — с другим покрытием и по прошествии некоторого времени измерить его износ, то на степень износа очевидно повлияет не только материал, но и то, как люди ухаживали за очками, факторы окружающей среды и другие причины. Следовательно, как и при анализе материала для подошв, наилучшим вариантом будет раздать всем очки, в которых на одно стекло будет нанесено одно покрытие, на второе стекло — другое покрытие (разумеется, это невозможно, если цвета покрытия отличаются). Стоит ли выбирать покрытие случайным образом или же можно всегда использовать покрытие А для правых стекол, покрытие В — для левых? Ученые, проводившие подобные эксперименты, говорят, что мы всегда начинаем протирать очки с одного и того же стекла. Тот, кто сначала чистит правое стекло, всегда чистит первым именно его, а то стекло, которое протирается первым, как правило, будет чище. Поэтому всегда лучше производить выбор случайным образом.
Сделайте это сами
Существуют городские легенды (кто знает, возможно, это не просто легенды), которые можно проверить с помощью статистики. Рассмотрим несколько примеров.
Помогает ли чайная ложка удержать газ в бутылке шампанского? Некоторые люди считают, что если опустить ложку в горлышко бутылки шампанского, то из нее не будет выходить газ (или по крайней мере он будет выходить медленнее, чем из открытой бутылки) и вино дольше сохранит свой вкус. Как развеять сомнения? Попробовать, то есть провести эксперимент. Эта задача похожа на задачу о дегустаторе чая. Можно попросить кого-нибудь попробовать шампанское из бутылки, в горлышко которой положили ложку, затем из бутылки с открытым горлышком. Мы уже знаем, что одного бокала из каждой бутылки недостаточно. Нужно налить минимум три бокала из одной бутылки и столько же — из другой. Бутылки должны быть полностью одинаковыми и должны храниться в одинаковых условиях. Единственная разница должна состоять в том, что в горлышко одной бутылки положили ложку. Вероятность случайно угадать все три бокала из бутылки, в горлышко которой положили ложку, равна 5 % (напомним, что три предмета из шести можно выбрать 20 разными способами, лишь один из которых является правильным). Чтобы снизить вероятность случайного угадывания, нужно предложить дегустатору больше бокалов, но следует учесть, что после определенного числа бокалов он уже не сможет четко различать вкус шампанского. Можно дать попробовать шампанское нескольким людям, но нужно быть внимательным: в этом случае вероятность случайного угадывания возрастет. Если вероятность того, что один человек точно укажет все три бокала, равна 5 %, то вероятность того, что один из пяти человек верно определит все три бокала, будет равна примерно 40 %, и сделать какие-то точные выводыбудет нельзя. Очевидно, что можно использовать прибор, измеряющий содержание газа в вине, и получить абсолютно точный результат. Однако не стоит забывать, что прибор может указать на различия, которые будут неощутимы на вкус, а между тем именно они представляют для нас интерес. Следовательно, вопреки показаниям прибора, класть ложку в горлышко бутылки не имеет смысла. По этой же причине не стоит доверять проведение эксперимента дегустатору вина, способному определять его вкус с исключительной точностью.
Умеете ли вы выбирать дыни? Задача о выборе спелой дыни еще больше похожа на задачу о дегустаторе чая. Некоторые люди утверждают, что умеют выбирать спелую дыню по весу, на звук и так далее. Чтобы определить, так ли это на самом деле, можно выбрать пять дынь случайным образом и предложить знатоку выбрать из них одну, по его мнению, самую спелую. Далее нужно взять по одной дольке из каждой дыни и снова предложить выбрать самую спелую, но теперь уже на вкус. Разумеется, в обоих случаях знаток должен указать одну и ту же дыню. Недостаток этого эксперимента заключается в том, что вероятность случайного угадывания равна 1/5 (20 %), следовательно, результат будет ненадежным. Однако вероятность случайного угадывания в двух случаях из двух составляет всего 4 %, в трех случаях из трех — 8 %, что крайне маловероятно, если знаток действительно не умеет выбирать спелые дыни.
Будут ли цветы стоять дольше, если добавить в воду аспирин? По-видимому, аспирин полезен не только для человека. Достаточно распространено мнение, что цветы будут стоять дольше, если добавить в воду аспирин. Чтобы проверить это экспериментально, можно взять два букета по 20 цветов (лучше если все цветы будут разными, то есть выбрать по две розы, две гвоздики, две маргаритки и так далее). Далее нужно поставить букеты в вазы и убедиться, что они находятся в абсолютно одинаковых условиях. Единственное различие будет заключаться в том, что в воду в одной вазе мы добавим немного аспирина, в другой — нет. Если эффект от аспирина отсутствует, вероятность того, что первым завянет определенный цветок, равна 50 %. Следовательно, крайне маловероятно, что во всех 20 случаях дольше простоят цветы в той вазе, куда был добавлен аспирин. Вероятность случайного совпадения равна вероятности выпадения решки 20 раз подряд при 20 бросках монеты. Применив правило «и» (см. главу 2), получим: 0,520 = 9,5·10-7 (порядка одной миллионной). Если цветы в вазах с аспирином будут стоять дольше, это будет очевидно доказывать эффективность аспирина. Вероятность того, что цветы в воде, куда был добавлен аспирин, будут стоять дольше минимум в 19 случаях, равна 2 на 10000; минимум в 15 случаях — порядка 2 %; в 14 случаях — почти 6 %. Следовательно, неудивительно, что цветы будут стоять дольше в воде, куда был добавлен аспирин, в 14 случаях и менее, даже если аспирин не оказывает абсолютно никакого эффекта. Приняв вероятность ошибки равной 5 % (эта величина называется уровнем значимости), аспирин следует считать эффективным, если цветы будут стоять дольше минимум в 15 случаях из 20.

Этот эксперимент очень прост, и в нем не учитывается, на сколько дольше сохраняется один цветок по сравнению с другим — на день, два дня или на неделю. Можно использовать и другие показатели, например критерий Уилкоксона, в котором учитывается разница во времени для каждой пары цветов. Однако важнее, чтобы эксперимент был проведен корректно, а его выводы не экстраполировались на другие случаи, нежели какой именно критерий мы выберем.
Действительно ли дорогие батарейки работают дольше? Когда мы покупаем бытовую технику, то помимо прочих факторов учитываем и ее внешний вид. Однако при покупке батареек единственный важный параметр — это время их работы. Любопытно проанализировать разницу в ценах между одинаковыми батарейками в зависимости от марки или магазина, где они были куплены. Обычные батарейки с напряжением 1,5 В от известных производителей могут стоить в два раза дороже батареек, купленных в дешевом супермаркете (и это совсем не значит, что там продаются только плохие батарейки). Также верно и то, что в последнее время известные производители предлагают различные скидки, и разница в цене уже не столь велика — рынок диктует свои правила. Правда ли, что дорогие батарейки работают дольше? И если они действительно работают дольше, то выгоднее ли покупать их? Иными словами, компенсирует ли разница во времени работы разницу в цене? Чтобы ответить на эти вопросы, нужны данные. Необходимо тщательно продумать алгоритмы сбора данных и проанализировать их нужным образом, чтобы получить достоверный результат. Иначе говоря, нужно использовать методы статистики. Задачу непросто решить по следующим причинам. * * *
КАК РАЗДЕЛИТЬ 20 МЫШЕЙ НА ДВЕ РАВНЫЕ ГРУППЫ СЛУЧАЙНЫМ ОБРАЗОМ? Допустим, мы хотим провести эксперимент на лабораторных мышах, чтобы сравнить, как различные диеты (обозначим их А и В) влияют на выносливость. У нас есть 20 мышей приблизительно одного возраста, их остальные характеристики также примерно равны. Мы делим их на две группы по 10 и кормим мышей каждой группы в соответствии с определенной диетой. По прошествии нескольких месяцев мы проводим эксперимент: помещаем мышей в воду и замеряем, сколько времени они смогут удержаться на поверхности, после чего вытаскиваем их из воды. Эксперимент показывает, что мыши, которых кормили по диете В, более выносливы, чем те, которых кормили по диете А: разница во времени, в течение которого мыши удерживались на поверхности воды, является статистически значимой и однозначно свидетельствует в пользу диеты В. Кажется, вы совершили открытие. Но как именно вы поделили мышей на группы? Разумеется, случайным образом: вы засовывали руку в клетку и «случайным образом» доставали 10 мышей по очереди. Эти мыши составили группу А, те, что остались в клетке, — группу В. Что-то не так? Разумеется. Мыши были разделены на группы не случайным образом. Когда мы достаем мышей из клетки, то, скорее всего, сначала мы достанем самых медленных, то есть самых слабых. Эти мыши образуют группу А, мыши из которой по итогам эксперимента оказались менее выносливыми. Но почему эти мыши оказались более медленными? Причина в диете или в том, что мы изначально собрали более медленных мышей в одной группе? Определить это нельзя. Вывод: важно гарантировать, что принцип формирования групп полностью случаен, например с помощью случайных чисел, бумажек или другим похожим способом. Если группы были сформированы не случайно, эту ошибку очень трудно исправить.* * * 1. Время работы и дорогих, и дешевых батареек варьируется. Их нельзя сравнивать по одной, так как время их работы гарантированно будет отличаться (если измерения будут проводиться с достаточной точностью), но это не означает, что если одна батарейка конкретного типа работает дольше, то и все батарейки этого типа будут в среднем работать дольше. 2. Если мы сформируем выборку батареек каждого типа и сравним среднее время работы по выборкам, то разница между средними значениями по выборкам также не будет однозначно свидетельствовать в пользу тех или иных батареек. Если обе группы будут состоять из батареек одной и той же марки, то и в этом случае среднее время работы в каждой группе будет различаться. Необходимо, чтобы разница во времени работы была статистически значимой. 3. Батарейки используются в разных устройствах и в разных режимах. Может оказаться так, что в одних устройствах они будут работать одинаковое время, в других — разное. 4. Измерить время работы батареек непросто. Мы не можем непрерывно день и ночь наблюдать за работой устройства. Можно выбрать определенное устройство и сравнить время работы для выборки дорогих и дешевых батареек. Можно подключить батарейку к лампочке и часам (электронные часы в этом случае не подходят) так, как показано на рисунке. Когда батарейка разрядится, стрелки часов остановятся, и мы сможем точно определить время работы батарейки. Нужно производить наблюдения минимум 1 раз в 12 часов, но в этих условиях батарейки проработают недолго.

Схема электрической цепи для измерения времени работы батарейки.
Для анализа полученных данных всегда рекомендуется использовать их графическое представление. Для небольшого объема данных, как в этом случае (например, для 10 батареек каждого типа), достаточно точечной диаграммы. Может случиться, что различия будут незаметны или диаграмма не позволит сделать однозначные выводы. Статистические тесты помогут нам подтвердить начальные предположения: результаты тестов не могут противоречить диаграмме.

Графическое представление трех возможных ситуаций.
Для анализа полученных данных подобным образом можно использовать t-критерий Стьюдента для независимых выборок. Это очень просто сделать с помощью Excel: нужно лишь указать, в каких ячейках находятся данные (первые два параметра функции «11 ЕСТ»), «хвосты» (третий параметр) и вид критерия (четвертый параметр функции). Третий параметр зависит от альтернативной гипотезы (нулевая гипотеза заключается в том, что различия отсутствуют). Если она такова, что более дорогие батарейки работают дольше (предположить это вполне логично), значение этого параметра будет равно 1. Если же альтернативная гипотеза заключается в том, что дорогие батарейки работают дольше или меньше, значение этого параметра будет равно 2. Четвертый параметр, вид критерия, указывает, являются ли выборки парными. Если выборки не парные, как в нашем примере, вариацию можно считать одинаковой в обеих выборках. Если графическое представление данных подобно указанному на точечных диаграммах выше, нетрудно заметить, что вариация одинакова. Если у вас возникли сомнения, можно указать, что вариация отличается, однако это почти не повлияет на результат.

Получение p-значения для t-критерия Стьюдента с помощью Excel.
В сомнительной ситуации, подобной той, что изображена на третьей диаграмме, по результатам теста p-значение равно 0,02 (нет смысла приводить его с такой точностью, как это делается в Excel). Как вы уже знаете, это означает, что если бы батарейки и того и другого типа в среднем работали одинаково, то разница, полученная по результатам эксперимента, была бы вызвана исключительно случайными факторами всего в 2 % случаев.
Действительно ли пакеты с водой отпугивают мух? Пластиковые пакеты, наполненные водой, — популярное средство для отпугивания мух (в Интернете упоминается, что этот способ используют везде, от Латинской Америки до Таиланда). Некоторые люди считают, что это средство работает, другие сомневаются. Любопытно, что те, кто верит в эффективность этого средства, приводят совершенно разные доводы: кто-то указывает, что луч света, проходящий через пакет с водой, раскладывается в спектр, и это сбивает с толку мух, так как их глаза устроены особым образом. Другие считают, что мухи не приближаются к воде, потому что знают: если они намокнут, то не смогут летать. Кто-то полагает, что пакеты с водой, напротив, используют в магазинах, так как они притягивают мух и те не мешают покупателям. Помогают ли пакеты с водой против мух или нет? Не вдаваясь в анализ причин и следствий, на этот вопрос можно ответить с помощью грамотно проведенного эксперимента. Однако провести его непросто. Нужно будет подсчитать число мух в комнате, где есть пакеты с водой, и в комнате, где их нет. Нужно выставлять пакеты с водой в определенные дни, выбранные случайным образом, и всякий раз подсчитывать число мух в помещении. Сосчитать мух нелегко, хотя нам могут помочь высокие технологии: некоторые фотоаппараты можно настроить так, что они будут делать снимок через заданные промежутки времени. Если делать снимки хорошим фотоаппаратом в комнате с белыми стенами, то мы сможем подсчитать число мух относительно точно. Однако этот метод обладает еще одним недостатком: если одни мухи вылетают из комнаты, а другие — влетают, это нельзя определить с помощью фотографий. Для подсчета мух в комнате также можно использовать липкую ленту. Читатель наверняка сможет предложить и другие способы. Верно одно: если мы не получим данные с помощью грамотно проведенного эксперимента, то не узнаем, насколько эффективны пакеты с водой против мух.
Библиография
BEHAR, R. у GRIMA, P., 55 Respuestas a preguntas típicas de estadistica, Madrid, Díaz de Santos, 2004. BLASTLAND, M. у DlLNOT, A., El tigre que no está. Un paseo por la jungla de la estadstíca, Madrid, Ed. Turner, 2009. GRIMA, P. (editor), Estadística en actión, publicado por la Facultad de Matemáticas у Estadística de la Universidad Politécnica de Cataluñia. Se puede descargar gratuitamente en: http://upcommons.upc.edu/e-prints/handle/2117/7810. PAULOS, J.A., El hombre anumérico, colección Metatemas, Barcelona, Tusquets, 1990. PEŇA, D., Fundamentos de estadística, Madrid, Alianza, 2001. SALSBURG, D., The Lady Tasting Tea. How Statistics Revolutionized Science in the Twentieth Century, Nueva York, W.H. Freeman, 2001. TANUR, J.M. ET AL., La estadística: una guía de lo desconocido, Madrid, Alianza, 1989. * * * Научно-популярное издание Выходит в свет отдельными томами с 2014 года Мир математики Том 13 Пере Грима Абсолютная точность и другие иллюзии. Секреты статистикиРОССИЯ Издатель, учредитель, редакция: ООО «Де Агостини», Россия Юридический адрес: Россия, 105066, г. Москва, ул. Александра Лукьянова, д. 3, стр. 1 Письма читателей по данному адресу не принимаются. Генеральный директор: Николаос Скилакис Главный редактор: Анастасия Жаркова Выпускающий редактор: Людмила Виноградова Финансовый директор: Наталия Василенко Коммерческий директор: Александр Якутов Менеджер по маркетингу: Михаил Ткачук Менеджер по продукту: Яна Чухиль Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ru, по остальным вопросам обращайтесь по телефону бесплатной горячей линии в России: 8-800-200-02-01 Телефон горячей линии для читателей Москвы: 8-495-660-02-02 Адрес для писем читателей: Россия, 105066, г. Москва, а/я 13, «Де Агостини», «Мир математики» Пожалуйста, указывайте в письмах свои контактные данные для обратной связи (телефон или e-mail). Распространение: ООО «Бурда Дистрибьюшен Сервисиз»
УКРАИНА Издатель и учредитель: ООО «Де Агостини Паблишинг» Украина Юридический адрес: 01032, Украина, г. Киев, ул. Саксаганского, 119 Генеральный директор: Екатерина Клименко Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ua, по остальным вопросам обращайтесь по телефону бесплатной горячей линии в Украине: 0-800-500-8-40 Адрес для писем читателей: Украина, 01033, г. Киев, a/я «Де Агостини», «Мир математики» Украïна, 01033, м. Кiев, а/с «Де Агостiнi»
БЕЛАРУСЬ Импортер и дистрибьютор в РБ: ООО «Росчерк», 220037, г. Минск, ул. Авангардная, 48а, литер 8/к, тел./факс: +375 17 331 94 27 Телефон «горячей линии» в РБ: + 375 17 279-87-87 (пн-пт, 9.00–21.00) Адрес для писем читателей: Республика Беларусь, 220040, г. Минск, а/я 224, ООО «Росчерк», «Де Агостини», «Мир математики»
КАЗАХСТАН Распространение: ТОО «КГП «Бурда-Алатау Пресс» Издатель оставляет за собой право увеличить рекомендуемую розничную цену книг. Издатель оставляет за собой право изменять последовательность заявленных тем томов издания и их содержание. Отпечатано в соответствии с предоставленными материалами в типографии: Grafica Veneta S.p.A Via Malcanton 2 35010 Trebaseleghe (PD) Italy Подписано в печать: 23.11.2013 Дата поступления в продажу на территории России: 15.04.2014 Формат 70 х 100 / 16. Гарнитура «Academy». Печать офсетная. Бумага офсетная. Печ. л. 4,5. Усл. печ. л. 5,832. Тираж: 200 000 экз. © Реге Grima, 2010 (текст) © RBA Collecionables S.A., 2011 © ООО «Де Агостини», 2014 ISBN 978-5-9774-0682-6 ISBN 978-5-9774-0706-9 (т. 13)
Примечания
1
В данном случае «сказать» намного легче, чем «сделать». Автору помогла его студентка Филипа да Силва.(обратно)
Последние комментарии
1 час 56 минут назад
2 часов 8 минут назад
2 часов 10 минут назад
2 часов 16 минут назад
2 часов 17 минут назад
2 часов 20 минут назад