Абсолютный минимум. Как квантовая теория объясняет наш мир [Майкл Файер] (fb2) читать онлайн

М. Файер. Абсолютный минимум. Как квантовая теория объясняет наш мир

Предисловие

Если вы читаете эту книгу, то, вероятно, относитесь к одной из двух категорий людей. Либо вы из числа моих коллег, посвящённых в тайны квантовой теории, и хотите посмотреть, как же кто-то смог написать серьёзную книгу по квантовой механике без математики. Либо вы принадлежите к тому большинству людей, кто смотрит на окружающий мир без ясного понимания того, почему многие повседневные вещи устроены именно так, а не иначе. При этом речь идёт далеко не о тех малозначительных аспектах нашей среды обитания, на которые можно было бы просто не обращать внимания. Напротив, это важные особенности нашего мира, которые никогда внятно не объясняются, поскольку кажется, что они лежат за пределами нашего понимания.

Что придаёт предметам их цвет, почему медный провод проводит электричество, а стекло нет, что же всё-таки такое транс-жиры и почему углекислота является парниковым газом, а кислород и азот — нет? Эти «белые пятна» в картине устройства вещей возникают вследствие кажущегося непреодолимым барьера, отделяющего нас от их понимания. Обычно этот барьер связан с математикой. Чтобы ответить на поставленные выше вопросы, а также на многие другие, необходимо понимание квантовой теории, но в действительности для этого не требуется математика.

Эта книга разовьёт вашу квантовую интуицию — и тем самым радикально изменит ваш способ восприятия окружающей действительности. Механику вы понимаете интуитивно, но знакомую вам механику мы называем классической. Когда в бейсболе делается длинный удар, вы знаете, что мяч сначала полетит вверх, а затем его траектория изогнётся и он упадёт на землю. Вы знаете, что если ударить по мячу сильнее, то он полетит быстрее и пролетит дальше, прежде чем упадёт. Почему мяч ведёт себя таким образом? Потому что на него действует гравитационное притяжение Земли. Вы смотрите на Луну и знаете, что она обращается вокруг Земли. Почему? Потому что гравитация притягивает Луну к Земле. Вам не надо садиться и решать ньютоновские уравнения движения, чтобы рассчитать, что произойдёт. Из повседневного опыта вы знаете, что яблоки падают вниз, а не вверх и что автомобилю, едущему быстрее, требуется больший путь, чтобы остановиться. Однако повседневный опыт не позволяет объяснить, почему вишня красная, а черника синяя. Цвет неразрывно связан с квантовомеханическим описанием молекул. Повседневный опыт не готовит нас к пониманию природы тех окружающих вещей, которые зависят от квантовых явлений. Как уже упоминалось здесь и подробно описывается в этой книге, понимание таких повседневных вещей, как цвет и электричество, требует квантовомеханического взгляда на природу.

Почему без математики? Представьте, что в этой книге изложение начиналось бы на вашем родном языке, потом переходило бы на латынь, а затем вновь возвращалось к исходному языку. Теперь представьте, что это переключение происходило бы всякий раз, когда начинаются подробные объяснения. Такие переходы с языка на язык, происходящие в книгах по квантовой механике, отличаются лишь тем, что они выполняются не между вашим языком и латынью, а между вашим языком и математикой. В серьёзных квантовомеханических книгах, например в моём собственном учебнике «Элементы квантовой механики» (Elements of Quantum Mechanics. Oxford University Press, 2001), вы будете постоянно встречать фразы такого рода: «данные взаимодействия описываются следующим набором спаренных дифференциальных уравнений». После уравнений в тексте будет сказано: «решения этих уравнений таковы», и далее последуют новые формулы. В этой книге, напротив, всё изложение является описательным. Диаграммы заменяют множество уравнений; исключение составляют лишь некоторые простые алгебраические формулы, которые детально объясняются. Однако и без обычного переизбытка математики фундаментальные философские и концептуальные основы приложений квантовой механики объясняются достаточно полно. Таким образом, каждый может достичь определённого уровня проникновения в квантовую теорию и углубить своё понимание окружающего мира. Если вы хорошо знаете математику, эта книга всё равно будет для вас полезной. Вы приобретёте концептуальное понимание, необходимое для перехода к математическому изложению квантовой теории. Если вы хотите получить некоторый объём умственной нагрузки, не связанной с математикой, эта книга познакомит вас с основами квантовой теории и с её приложениями к физике атомов и молекул.

1. Кот Шрёдингера

Почему вишня красная, а черника синяя? Что подразумевается под понятием «размер»? Кажется, что эти два вопроса совершенно не связаны между собой, а второй вопрос вообще не имеет смысла. Разве мы не знаем, что такое размер? Одни вещи большие, другие маленькие. Но развитие квантовой теории показало, что эти два вопроса тесно взаимосвязаны и что до двадцатых годов прошлого века мы опирались на совершенно неверное понимание размера.

Наше представление о размере, когда мы вообще об этом задумываемся, отлично работает в повседневной жизни. Однако начиная примерно с 1900 года та физика, которая описывает все происходящие в природе процессы, и та, что прекрасно подходит для обеспечения посадки космических аппаратов на Марс, стали расходиться между собой. В итоге принципиально новое понимание размера понадобилось не только для объяснения того, почему вишня красная, а черника синяя, но и для понимания устройства молекул, составляющих наши тела, и микроэлектроники, обеспечивающей работу наших компьютеров, для объяснения, почему углекислый газ является парниковым и как электричество течёт по металлам.

Повседневный опыт учит нас мыслить в понятиях классической физики, которая была значительно развита и формализована Исааком Ньютоном (1642–1727). Всё, что мы узнаём с раннего детства, подготавливает нас к принятию фундаментально ошибочного представления о природе. Эта книга посвящена понятию абсолютного размера и вытекающей из него квантовой теории, которая требует кардинально изменить способ мышления о природе. В первой половине книги описываются основные понятия квантовой теории, а во второй эта теория применяется для объяснения многих особенностей мироустройства через анализ свойств атомов и молекул, а также их роли в повседневной жизни.

Начало работе над этой книгой положил простой вопрос: можно ли понять квантовую механику с позиций здравого смысла? Мне задали его на фестивале науки «Вондерфест-2005», проводимом при поддержке физического факультета Калифорнийского университета в Беркли и химического факультета Стэнфордского университета. «Вондерфест» — это ежегодное мероприятие, на котором читаются лекции для широкой публики о последних достижениях в самых разных дисциплинах. Однако меня попросили подготовить выступление не о последних достижениях в моей области исследований, а на тему: «Можно ли понять квантовую механику с позиций здравого смысла», поскольку споры на эту тему с участием как учёных, так и непрофессионалов не утихают с самого появления квантовой теории в 1900 году. Причём на то, чтобы представить свой утвердительный ответ на данный вопрос, у меня было всего полчаса. Задача оказалась чрезвычайно трудной, так что я в течение нескольких месяцев размышлял на эту тему и потратил уйму времени на подготовку к лекции. Несмотря на это, я считал, что моё выступление провалилось, — не потому, что такие важные вопросы невозможно разъяснить неспециалистам, но из-за жёстких ограничений по времени. Чтобы добраться до сути дела, необходимо ввести некоторые понятия, позволяющие чётко обозначить различия между классической и квантовой механикой.

Эта книга — моя попытка уделить квантовому описанию природы достаточно времени, чтобы вынести о нём предметное суждение. Используемая в книге математика очень проста — не сложнее элементарных формул. Идея состоит в том, чтобы сделать квантовую теорию полностью доступной для неспециалиста. Тем не менее тот факт, что книга практически не требует знания математики, не означает, что её материал прост. Читать Кьеркегора^{1} совсем непросто, хотя для этого и не требуется математических знаний. Однако, в отличие от работ Кьеркегора, смысл представленного здесь материала должен быть ясен всякому читателю, готовому приложить небольшое мыслительное усилие.

Классическая механика описывает движение бейсбольного мяча, вращение волчка и полёт аэроплана. Квантовая механика описывает движение электронов и форму молекул, скажем, ненасыщенных жиров, а также электропроводность и сверхпроводимость. Классическая механика — это ограниченная версия квантовой механики. Квантовая механика содержит классическую, но не наоборот. В этом смысле классическая механика неверна. Однако мы используем её при создании мостов, автомобилей, самолётов и плотин, не тревожась о том, что при их конструировании не использовалось более общее описание природы, заложенное в квантовой механике. Использование классической механики не приводит к обрушению мостов, автоавариям, падениям самолётов или прорывам плотин. В своей области, то есть в применении к механике, с которой мы сталкиваемся в повседневной жизни, классическая теория работает безупречно.

Наше интуитивное ощущение того, как устроен мир, основывается на повседневном опыте, и этот опыт в основном классический. Тем не менее даже в повседневной жизни классическая механика не может объяснить, почему молекулы, содержащиеся в чернике, делают её синей, а молекулы, содержащиеся в вишне, придают ей красный цвет. Интуиция, которая вырабатывается в течение всей нашей жизни благодаря наблюдениям за определёнными проявлениями природы, приводят к тому, что мы оказываемся не готовы принять другие её аспекты, даже несмотря на то что эти аспекты пронизывают всю нашу повседневную жизнь.

Кот Шрёдингера

Кота Шрёдингера часто используют в качестве иллюстрации парадоксов, которыми, как кажется, пропитано квантовомеханическое описание природы. Эрвин Шрёдингер (1887–1961) и Поль Дирак (1902–1984) получили Нобелевскую премию по физике в 1933 году за вклад в разработку квантовой теории, в особенности

«за открытие новых плодотворных форм атомной теории».

Шрёдингеру никогда не нравилась трактовка той математики, которая является фундаментальной первоосновой квантовой теории. Идеи, тревожившие Шрёдингера, как раз и являются предметом обсуждения в этой книге. Ставший знаменитым «кот Шрёдингера» служил ему в качестве иллюстрации некоторых беспокоивших его проблем. У нас кот Шрёдингера появляется в модифицированной версии просто для того, чтобы показать, что квантовая механика кажется лишённой смысла, если обсуждать её с использованием обыденных житейских понятий. Рассматриваемые здесь коты служат для того, чтобы докопаться до сути дела, и отличаются от первоначальной шрёдингеровской версии, которая является более эзотерической. К описываемому сценарию мы ещё вернёмся в дальнейшем. Он будет обсуждаться как аналогия реальных экспериментов, объяснённых квантовой теорией, но не как реальный физический пример работы квантовой механики.

Представьте себе, что перед вами выставили 1000 ящиков и в процессе эксперимента вы должны их вскрыть. Вам сказали, что в каждом ящике находится наполовину мёртвый кот, так что при вскрытии первой попавшейся коробки вы рассчитываете увидеть очень больное животное. В действительности сказанное вам требует пояснения. Корректное утверждение состоит не в том, что все коты полумёртвые, а в том, что каждый из них находится в состоянии, в котором он одновременно абсолютно мёртв и полностью здоров. Это смесь смерти и здоровья в пропорции 50:50. Другими словами, есть 50-процентная вероятность того, что кот мёртв, и 50-процентная вероятность того, что он жив. Каждый из тысячи котов в этой тысяче ящиков находится в точности в одном и том же состоянии. Квантовый экспериментатор, который подготовил все эти ящики, не помещал в 500 ящиков 500 мёртвых котов, а в остальные 500 ящиков ещё 500 живых котов. Вместо этого он поместил во все ящики одинаковых котов, каждый из которых представляет собой некую смесь 50 на 50 мёртвого и совершенно здорового кота. Пока коты заперты в ящиках, они не изменяются и остаются в смешанном мёртво-живом состоянии. Далее вам говорят, что, вскрыв ящик, вы определите судьбу кота. Сам акт осмотра, нацеленный на то, чтобы увидеть, жив ли кот, предопределяет, жив он или мёртв.

Вы открываете первый ящик и обнаруживаете совершенно здорового кота. Заглядываете в следующие три ящика и находите мёртвых котов. Вскрываете ещё один ящик и видите живого кота. Когда вскрыта тысяча ящиков, у вас 500 живых и 500 мёртвых котов. Возможно, вы удивитесь ещё сильнее, когда повторите всё то же самое с новой тысячей ящиков, содержащих смесь 50 на 50 мёртвых и абсолютно здоровых котов. Если вы откроете ящики в том же порядке, как и в первый раз, то не обязательно получите тот же самый результат для каждого отдельного ящика. Скажем, в первый раз при проверке ящика номер 10 обнаружился живой кот. При втором заходе вы можете найти в нём мёртвого кота. Первый прогон эксперимента не даёт никакой информации о том, что будет содержать каждый ящик во второй раз. Однако после того, как вскрыта вся тысяча ящиков, во втором заходе вы вновь получите 500 живых котов и 500 мёртвых.

Я должен признаться, что допустил некоторое упрощение. В двух заходах эксперимента со шрёдингеровскими котами вы, вероятно, не получите каждый раз ровно по 500 живых и 500 мёртвых котов. Эта ситуация чем-то похожа на 1000-кратное бросание идеальной монеты. Поскольку вероятность выпадения решки равна одной второй и вероятность выпадения орла — тоже одна вторая, после 1000 бросаний вы получите около 500 решек. Однако у вас может также выпасть 496 или 512 решек. Вероятность получить ровно 500 решек и 500 орлов при 1000 бросаний составляет 0,025 (2,5 %). Вероятность выпадения 496 решек равна 0,024 (2,4 %), а 512 решек — 0,019 (1,9 %). Вероятность получить только 400 решек или 400 живых котов при 1000 попыток составляет 4,6∙10⁻¹¹ = 0,000000000046. Таким образом, возможные исходы сосредоточены вблизи 500 из 1000, или 50 %. Зная, что имеется 1000 ящиков со шрёдингеровскими котами, которые представляют собой смесь 50 на 50 мёртво-живых котов, или 1000 раз бросая идеальную монету, вы не можете сказать, что случится при вскрытии одного конкретного ящика или при отдельном бросании монеты. На самом деле нельзя даже точно сказать, что случится, когда вы откроете всю тысячу ящиков или 1000 раз подбросите монету. Можно говорить лишь о том, какова вероятность получить определённый результат для одного события и каким будет наиболее вероятный совокупный результат множества событий.

Не так, как при бросании монеты

Существует принципиальная разница между котами Шрёдингера, или, более строго, реальными квантовыми экспериментами, и бросанием монеты. Перед броском монета повёрнута вверх либо орлом, либо решкой. Бросая её, я не знаю, каким будет исход, но монета начинает движение из хорошо определённого состояния — вверх либо орлом, либо решкой — и заканчивает тоже в хорошо определённом состоянии — орёл или решка. Можно построить машину, которая подбрасывает монету настолько точно, что при падении та всегда даёт один и тот же результат. Никакие законы природы этому не препятствуют. Кладя монету в машину решкой вверх, можно переключателем задать, как именно она должна выпасть — орлом или решкой. Когда монету бросают рукой, нельзя абсолютно точно повторить движение, что и делает исход случайным. Однако ящик, содержащий кота Шрёдингера, — это совсем другое дело. Кот является смесью живого и мёртвого в соотношении 50 на 50. Именно акт вскрытия ящика и наблюдения состояния кота заставляет последнего перейти из «смешанного состояния» в «чистое» — либо живое, либо мёртвое. Не имеет значения, как именно открываются ящики. В отличие от случая с монетами машина, построенная для открывания всей тысячи ящиков в точности одинаковым способом, не приведёт к получению одинаковых результатов. Единственное, что известно при вскрытии любого ящика, — то, что с вероятностью 50 % в нём обнаружится живой кот.

Реальные явления могут вести себя подобно шрёдингеровским котам

Как уже отмечалось, с проблемой кота Шрёдингера нельзя столкнуться в жизни. Однако многие частицы и состояния ведут себя подобно тому, что происходит при открывании ящиков с котами Шрёдингера. Частицы, такие как фотоны (частицы света), электроны, атомы и молекулы, обладают «смешанными состояниями», которые при наблюдении превращаются в «чистые состояния», аналогично тому, как это было описано для случая с котами Шрёдингера. Сущности, лежащие в основе привычных нам веществ, процессов и явлений, на фундаментальном уровне ведут себя столь же контринтуитивно, как шрёдингеровские коты. Однако проблема заключается не в поведении электронов и атомов, а скорее в нашем интуитивном представлении о том, как вещи должны себя вести. Наша интуиция основана на повседневном опыте. Мы получаем информацию посредством чувств, позволяющих наблюдать лишь те явления, в которых поведение материи подчиняется законам классической механики. Чтобы принять кванотовомеханический мир, который окружает нас повсюду, но который мы не можем понять интуитивно на основе наших сенсорных восприятий, необходимо выработать новое понимание природы и новую интуицию.

2. Размер абсолютен

Фундаментальная природа размера имеет решающее значение для понимания различий между теми аспектами повседневной жизни, которые согласуются с нашим интуитивным восприятием природы, и миром квантовых явлений, которые тоже окружают нас. Мы хорошо чувствуем, как движутся бейсбольные мячи, но, как правило, склонны недооценивать степень своего незнания относительно того, что придаёт вещам различный цвет и почему нагревательный элемент электрокамина становится горячим и от него исходит красное свечение. Движение бейсбольных мячей можно описать, используя законы классической механики, но цвет и электрический нагрев — квантовые явления. Разница между классическими и квантовыми явлениями непосредственно связана с определением размера.

Корректным представлением о размере является кванотовомеханическое, и оно сильно отличается от привычного нам. Зато наше обыденное представление о размере играет центральную роль в классической механике. Неправильная трактовка понятия размера и все последствия этой ошибки ответственны, в конечном счёте, за неспособность классической механики правильно описывать и объяснять поведение фундаментальных составляющих материи. Квантовомеханическое описание материи лежит в основе технологий в столь разных областях, как микроэлектроника и создание фармацевтических препаратов.

Размер в повседневной жизни

В классической механике размер относителен. В квантовой механике размер абсолютен. В чём состоит разница между относительным и абсолютным размером и почему она так важна?

В классической механике и в повседневной жизни мы определяем, велик предмет или мал, сравнивая его с каким-то другим предметом. На рис. 2.1 изображены два камня. Взглянув на них, мы скажем, что левый камень больше правого. Однако поскольку их не с чем больше сравнить, мы не можем понять, большие это валуны или мелкие камешки. На рис. 2.2 снова изображён левый камень, однако на этот раз размер камня очевиден, поскольку его можно сопоставить с размером человеческой руки. Зная, какова характерная величина руки, мы получаем ясное представление о размере камня. Как только у нас появился объект для сравнения, мы получили возможность определить, что этот камень небольшой, хотя и не совсем мелкий. Если я стану описывать этот камень по телефону, то скажу, что он немного больше кисти руки, и этого достаточно, чтобы мой собеседник понял, насколько он велик. Если же никакого объекта известной величины для сравнения нет, то нет и возможности определить размеры.

Рис. 2.1. Два камня

Из рис. 2.1 видно, до какой степени мы полагаемся на сравнение предметов друг с другом при определении их размеров. Два камня на рис. 2.1 изображены на белом фоне, и их не с чем сопоставить. Их близость заставляет нас немедленно сравнить их и заключить, что левый камень больше правого. На рис. 2.3 камень, который на рис. 2.1 расположен справа, изображён в своём естественном окружении. Теперь мы видим, что на самом деле это очень большой камень. Рука на камне позволяет однозначно судить о его размерах. Как и рука, держащая камень на рис. 2.2, рука, лежащая на камне, задаёт нам масштаб, позволяющий выполнить относительное определение размеров. Мы узнаём, насколько велик предмет, сравнивая его с чем-нибудь другим.

Рис. 2.2. Камень, изображённый на рис. 2.1 слева, в руке человека

Рис. 2.3. Камень, изображённый на рис. 2.1 справа, в окружении, позволяющем судить о его размерах

Метод наблюдения имеет значение

Почему важно, как определяется размер — относительно или абсолютно? Дело в том, что для наблюдения объекта с ним надо взаимодействовать. Это справедливо как в случае классической, так и в случае квантовой механики.

Рисунок 2.4 иллюстрирует процесс наблюдения за розой. В абсолютно тёмной комнате розу увидеть нельзя. Однако на рисунке на розу падает свет, испускаемый лампочкой. Часть света поглощается, а часть отражается. (Какие цвета поглощаются, а какие отражаются, придавая листьям зелёную окраску, а лепесткам розовую, — это вопрос из области квантовой механики, который мы обсудим в главе 8.) Часть света, испытавшего отражение, воспринимается глазом и обрабатывается мозгом — это и есть процесс наблюдения за розой. Наблюдатель взаимодействует с розой посредством света, который от неё отражается.

Рис. 2.4. Лампочка освещает розу. Свет, отражаясь от розы, попадает в глаз, позволяя нам видеть розу

Поняв, что наблюдение за объектом предполагает взаимодействие с ним, мы готовы определить большое и малое. Определения того, что является большим, а что — малым, одинаковы в классической и квантовой механиках. Если вызванное наблюдением (что является другим названием для измерения) возмущение объекта пренебрежимо мало, то объект большой. Если этим возмущением пренебрегать нельзя, то объект маленький. В классической механике делается следующее допущение.

Допущение: при выполнении наблюдения всегда можно найти способ произвести пренебрежимо малое возмущение.

Если поставить корректный эксперимент, то возмущение, сопутствующее измерению, будет ничтожным. Тем самым можно наблюдать систему, не изменяя её. Однако если поставить эксперимент по изучению системы неправильно, то возмущение не будет пренебрежимо малым и объект окажется маленьким. Подобные возмущения определённым образом меняют систему, и желательно по возможности выполнять измерения так, чтобы не менять то, что подвергается измерению. В классической теории предполагается, что величину возмущений можно сделать сколь угодно малой. Независимо от того, что наблюдается, можно найти экспериментальный метод, вызывающий ничтожные возмущения. Из этой предполагаемой возможности найти экспериментальный метод, дающий пренебрежимо малое возмущение, вытекает, что размер является лишь относительным. Размер объекта зависит от самого объекта и вашего измерительного метода. Он не является неотъемлемым свойством объекта. Любой объект можно считать большим, если наблюдать его корректным методом, вызывающим пренебрежимо малые возмущения.

Допустим, вы решили проверить стену своей комнаты, бросая в неё множество бильярдных шаров. В этом эксперименте вы будете наблюдать, где упадёт шар, отскочив от стены. Вы начинаете бросать шары, и очень скоро вся комната оказывается усыпанной штукатуркой. На стене появляются выбоины, и шары, которые вы бросаете позднее, отскакивают уже не так, как первые. Это неудивительно и вызвано повреждениями, которые нанёс стене ваш метод измерения. Вы приходите к выводу, что это не самый лучший эксперимент по наблюдению стены. Вызвав хорошего штукатура, который приводит стену в исходное состояние, вы начинаете заново. На этот раз вы решаете осветить стену и наблюдать отражённый ею свет. Вы обнаруживаете, что этот метод отлично работает и позволяет вам разглядеть стену во всех деталях. Проводя наблюдения с помощью света в течение продолжительного времени, вы убеждаетесь, что видимые характеристики стены не изменяются.

Большое или малое — это величина возмущений

В случае, когда стена наблюдалась с помощью бильярдных шаров, она была маленькой, поскольку такое наблюдение приводило к существенным возмущениям. При наблюдении стены с помощью света она была большой — такое наблюдение вызывало ничтожные возмущения. В этих экспериментах, которые хорошо описываются классической механикой, размеры стены относительны. Поставьте плохой эксперимент (наблюдение с помощью бильярдных шаров), и стена будет маленькой. Поставьте хороший эксперимент (наблюдение с помощью света), и она окажется большой.

В классической механике размеры не являются собственной характеристикой объекта. Придумайте правильный эксперимент, и любой объект окажется большим. Задача экспериментатора — разработать и осуществить такой эксперимент. Ничто в теоретической классической механике не препятствует постановке подобного хорошего эксперимента, который вызывает ничтожные возмущения в процессе измерения. Другими словами, хороший эксперимент не меняет наблюдаемый объект, а значит, наблюдению подвергается большой объект.

Причинность для больших объектов

Возможность сделать большим любой объект важна потому, что в таком случае за ним можно наблюдать, не изменяя его. Наблюдение объекта без его изменения тесно связано с понятием причинности в классической механике. Причинность можно определять и использовать разными способами. Одна из формулировок, определяющих причинность, состоит в том, что одинаковые причины вызывают одинаковые последствия. Отсюда вытекает, что свойства любой системы определяются предшествующими событиями в соответствии с законами физики. Другими словами, если вы знаете во всех подробностях предшествующую историю системы, то сможете узнать её текущее состояние и то, как оно изменится в будущем. Идея причинности привела Пьера-Симона, маркиза де Лапласа (1749–1827), одного из самых прославленных физиков и математиков, к утверждению о том, что если знать с абсолютной точностью текущее состояние всего мира, то можно рассчитать его состояние в любой момент в будущем. Конечно, мы не можем совершенно точно знать состояние всего мира, но для многих систем классическая механика позволяет очень точно предсказывать последующие события, опираясь на знание текущего состояния системы. Предсказание траектории снаряда для прицельной артиллерийской стрельбы и предсказание солнечных затмений — примеры того, как хорошо работает причинность в классической механике.

В качестве простого, но очень важного примера рассмотрим траекторию свободной частицы, например камня, летящей в космосе. Свободная частица — это объект, на который не действуют никакие силы — ни сопротивление воздуха, ни гравитация, ни что-то ещё. Физикам нравится обсуждать свободные частицы, поскольку это простейшие из всех возможных систем. Важно, однако, отметить, что по-настоящему свободных частиц в природе не бывает. Даже камень в межгалактическом пространстве испытывает слабое влияние гравитации и слабое воздействие падающего на него света, а также сталкивается иногда с атомами водорода, рассеянными среди галактик. Тем не менее свободные частицы полезно обсудить, и их можно с хорошим приближением воспроизвести в лаборатории, так что мы обсудим гипотетическую истинно свободную частицу, несмотря на невозможность её существования.

Допустим, некоторое время назад свободная частица была приведена в движение с импульсом p, и в момент времени, который мы будем называть нулевым (t=0), она находится в положении x. Пусть x — это координата частицы по горизонтальной оси. На рис. 2.5 показана траектория нашего камня начиная с t=0. Его импульс равен p=m∙V, где m — масса объекта, а V — скорость движения. На Земле масса — это обычный вес^{2}. Однако если камень окажется на Луне, масса его не изменится, но вес составит одну шестую земного, из-за того что сила притяжения на Луне меньше, чем на Земле.

Рис. 2.5. Свободная частица, представленная здесь камнем, движется по своей траектории

Чисто качественно понятие импульса можно описать как меру силы, с которой объект способен воздействовать на другой объект в случае столкновения. Представим себе маленького мальчика весом 20 кг, бегущего и врезающегося в вас со скоростью 20 км/ч. Он, возможно, собьёт вас с ног. Теперь представьте себе 80-килограммового мужчину, который сталкивается с вами на скорости 5 км/ч. Он, вероятно, тоже вас собьёт. Мальчик лёгкий, но бежит быстро. Мужчина тяжёлый, но движется медленно. Оба они обладают одинаковым импульсом 400 кг∙км/ч. В некотором смысле оба они при столкновении окажут на вас одинаковое воздействие. Конечно, этот пример не следует воспринимать слишком буквально. Мальчик может удариться о ваши ноги, тогда как мужчина натолкнётся на вашу грудь. Однако если отвлечься от подобных различий, то в обеих ситуациях результат столкновения будет одинаковым.

Импульс — это вектор, поскольку скорость является вектором. Вектор имеет величину и направление. Скорость — это быстрота и направление. Ехать со скоростью 100 км/ч на север — это не то же самое, что ехать со скоростью 100 км/ч на юг. Темп движения одинаковый, но направления различаются. Импульс численно равен произведению m∙V и имеет направление, поскольку направление есть у скорости. На рис. 2.5 движение происходит слева направо.

В момент t=0 мы наблюдаем (измеряем) положение и импульс камня. Зная x и p в момент t=0, можно предсказать траекторию камня для всех последующих моментов. Предсказать траекторию свободной частицы очень просто. Поскольку на неё не действуют никакие силы — ни тормозящее её сопротивление воздуха, ни притягивающая к Земле гравитация, — частица будет бесконечно двигаться по прямой линии. К некоторому более позднему моменту t´ (t-штрих), t=t´, камень переместится на расстояние d=V∙t´, равное произведению скорости на продолжительность движения частицы. Поскольку в момент старта t=0, время движения частицы составит t´, скажем одну секунду, так что мы точно знаем, где искать камень в момент t´. Можно выполнить наблюдение и посмотреть, находится ли частица там, где она должна быть, — конечно, она там и окажется (см. рис. 2.5). Можно предсказать, где она будет в последующие моменты времени, и убедиться, что она действительно туда попадёт (см. правую часть рис. 2.5). Мы предсказали, где будет частица, и, выполнив наблюдение, обнаружили её там. Она движется по хорошо определённой траектории, и принцип причинности строго соблюдается.

Возмущения, которыми нельзя пренебречь, — это важно

Обратимся теперь к рис. 2.6. Камень подготовлен так же, как на рис. 2.5. В момент t=0 он имеет координату x и импульс p. Следующий момент наблюдения t=t´.

Положение камня предсказывается по значениям x и p в момент t=0. Однако через некоторое время после момента t=t´ в камень врезается птица. (Простите меня за то, как она нарисована, — это лучшее, что я смог изобразить с помощью мыши.) На жаргоне физиков это называется событием рассеяния камня на птице. Столкнувшись с камнем, птица вызывает возмущение, которым нельзя пренебречь. Неудивительно поэтому, что измерения положения и импульса, выполненные после события рассеяния, не будут соответствовать предсказаниям, сделанным на основе траектории, определённой в момент t=0. Согласно допущениям классической механики, если мы всё знаем о птице, камне и их взаимодействии (столкновении друг с другом), то можем определить, что случится после рассеяния камня на птице. Можно проверить наши предположения посредством наблюдения. Наблюдение в классической механике возможно благодаря тому, что всегда существует метод наблюдения, вызывающий ничтожно малые возмущения системы, то есть способ сделать систему большой. Однако суть дела в том, что предсказания, основанные на знании траектории, которая была определена до появления непренебрежимо малого возмущения, перестают после него сбываться, и это, конечно, неудивительно.

Рис. 2.6.Свободная частица, представленная здесь камнем, движется по некоторой траектории. В момент t=0 она характеризуется положением x и импульсом p. В последующий момент времени t=t´ она перемещается в новое положение, где подвергается наблюдению, на основе которого предсказывается её будущее движение. Однако спустя некоторое время в камень врезается птица. Предсказание, сделанное в момент t´, более не работает

Возмущение есть всегда

Квантовая теория фундаментально отличается от классической механики своей трактовкой понятий размера и экспериментального наблюдения, благодаря чему размеры становятся абсолютными. Дирак сжато сформулировал допущение, делающее размеры абсолютными.

Допущение: существует предел точности наших наблюдений и малости сопутствующих возмущений, предел, заложенный в природу вещей, который невозможно обойти за счёт усовершенствования техники или опыта на стороне наблюдателя.

Этот тезис категорически несовместим с классическим мышлением. Он утверждает, что, наблюдая (измеряя) систему, вы всякий раз вызываете возмущение — оно может быть мало, но оно всегда есть. Причём величина возмущения определяется самим устройством природы. Никакое усовершенствование инструментов, никакие новые методы наблюдения не позволят исключить или уменьшить это минимальное возмущение.

У тезиса Дирака есть следствия, которые включаются во все формулировки квантовой механики. Его допущение немедленно делает размеры абсолютными. Объект велик в абсолютном смысле, если минимальное возмущение, которым сопровождается измерение, пренебрежимо мало. Объект мал в абсолютном смысле, если его неустранимое минимальное возмущение не является пренебрежимо малым. На самом фундаментальном уровне классическая механика не приспособлена для описания объектов, малых в абсолютном смысле. В классической механике любой объект можно сделать «большим», найдя подходящий эксперимент для выполнения наблюдений. При разработке классической механики никогда не предполагалось, что в силу неотъемлемых свойств природы невозможно так усовершенствовать методику, чтобы наблюдения не меняли систему. Поэтому классическая механика неприменима к объектам, малым в абсолютном смысле. Неспособность классической механики работать с абсолютно малыми объектами, такими как электроны и атомы, является причиной, по которой её применение для описания подобных объектов приводит к ошибкам.

Рисунок 2.7 поясняет суть проблемы. Электрон — частица, малая в абсолютном смысле. (В дальнейшем мы подробно обсудим значение слова «частица», которое здесь отличается от классического представления о частицах.) В момент t=0 электрон движется вдоль траектории. Как и в случае с камнем, мы хотим выяснить, ведёт ли он себя так, как мы ожидаем, то есть позволяет ли он нам делать соответствующие предсказания. Воспользуемся методом наблюдения электрона, создающим наименьшие помехи: пусть он взаимодействует с одиночной частицей света — фотоном. (Далее мы подробно обсудим природу света и смысл, который вкладывается в понятие «частица света».) Вот чем эта проблема кардинально отличается от той, что показана на рис. 2.5.

Поскольку электрон абсолютно мал, даже когда он наблюдается с помощью единственной частицы света, это вызывает возмущение, которым нельзя пренебречь. Электрон изменяется наблюдением. Мы не можем предсказывать его поведение в дальнейшем, если пронаблюдали его, чтобы увидеть, делает ли он то, что мы от него ожидали. Причинность работает с невозмущёнными системами. Акт наблюдения электрона возмущает его. Вы можете предсказать поведение системы, пока не смотрите на неё, чтобы убедиться, что она действительно ведёт себя так, как, по вашему мнению, она должна себя вести. Поэтому причинность неприменима к абсолютно малым системам. Они ведут себя так, что наблюдение разрушает причинность. Недетерминированность, которая является частным случаем неопределённости, появляется в расчётах наблюдаемых величин в случае абсолютно малых систем. Система абсолютно мала, если минимальное возмущение, сопровождающее измерение, не является пренебрежимо малым. Абсолютно малую систему нельзя наблюдать, не изменяя её.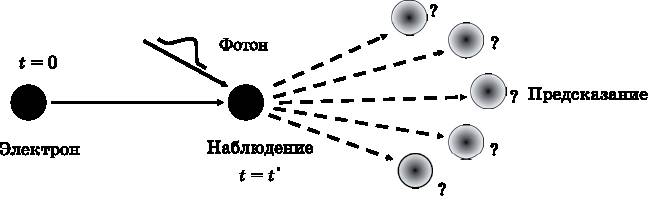

Рис. 2.7.В момент t = 0 электрон движется по некоторой траектории. В момент t = t´ мы наблюдаем его наименее возмущающим способом, позволяя ему взаимодействовать с одиночной частицей света — фотоном. Взаимодействие электрона с фотоном вызывает возмущение, которым нельзя пренебречь. Невозможно использовать причинность для предсказания того, что случится после наблюдения

Нельзя рассчитать будущее — только вероятности

В отличие от классической механики, как только квантовая система подвергается наблюдению, становится невозможно сказать, какой результат даст следующее наблюдение. Этот недостаток точности отличается от того, что возникает при столкновении птицы с камнем (см. рис. 2.6). В случае птицы и камня принципиально возможно, хотя и трудно, предсказать результат следующего наблюдения. Нам понадобится знать все свойства птицы и камня, а также все подробности, касающиеся того, как птица сталкивается с камнем (например, скорость и массу птицы и камня, а также угол, под которым происходит их столкновение).

В случае электрона и фотона нельзя точно предсказать, каким будет результат следующего наблюдения. Возможности квантовой теории ограничиваются предсказанием вероятности получения конкретного результата. В примере с котами Шрёдингера при вскрытии ящика обнаруживался либо живой, либо мёртвый кот. И не было способа предсказать, каким он будет. Вскрытие ящика (наблюдение кота) переводит кота из своего рода смешанного состояния живого и мёртвого в одно из чистых состояний — либо живое, либо мёртвое. При вскрытии множества ящиков вероятность обнаружить живого кота составляла 50 %, но не было способа предсказать, что случится при вскрытии конкретного ящика (при единичном измерении).

Эксперимент с котом нельзя реализовать физически, а значит, он не является подлинной квантовомеханической задачей. Реальная физическая задача, подобная задаче с котом, обсуждается далее. Задача с котом предназначалась для первоначального введения идеи о том, что наблюдение способно менять систему и что лишь вероятность может быть определена из серии экспериментов. Для реальных систем, которые являются абсолютно малыми, квантовая механика — это теория, позволяющая вычислить и понять распределение вероятности, получаемое при выполнении измерений на множестве одинаково приготовленных систем. Каким образом возникают квантовомеханические распределения вероятности и как представлять себе природу возмущений, которые сопутствуют измерениям абсолютно малых систем, вы узнаете в следующих главах.

3. Кое-что о волнах

Для того чтобы разобраться в природе неустранимых возмущений, которые сопутствуют измерению, и понять, что можно, а что нельзя измерить у абсолютно малой квантовомеханической системы, необходимо сначала потратить некоторое время на обсуждение классических волн и классического описания света. В начале XX века был проведён ряд экспериментов, результаты которых не удавалось объяснить с помощью классической механики. Самый первый из них был связан со светом. Тем не менее сначала мы обсудим эксперимент, который, как может показаться, демонстрирует, что классические идеи прекрасно работают. Далее, в главе 4, мы расскажем об одном из экспериментов, показывающих, что описание с позиций классической механики не может быть корректным и, более того, что классическая реинтерпретация эксперимента, которая кажется работоспособной, на самом деле никуда не годится. И наконец, будет дан корректный анализ эксперимента со светом, основанный на квантовых идеях, что вернёт нас к котам Шрёдингера.

Что такое волны?

Существует много видов классических волн: волны на воде, звуковые волны, световые (электромагнитные) волны. Все волны имеют ряд общих характеристик, таких как амплитуда, длина волны, скорость и направление распространения (направление, в котором движется волна). На рис. 3.1 показана волна, движущаяся в направлении x. Амплитуда волны — это «расстояние» между её положительным и отрицательным пиками по направлению сверху вниз^{3}. Длина волны — это расстояние вдоль направления её распространения между двумя положительнымиили отрицательными пиками, то есть это расстояние, через которое волна повторяет саму себя. Если, оседлав волну, вы сместитесь на любое целое число длин волн вперёд или назад вдоль неё, то для вас ничего не изменится. Любая волна движется с определённой скоростью V.

Волны характеризуются скоростью и частотой

Скорость волны зависит от её типа, и эта характеристика требует небольшого обсуждения. Представьте себе, что стоите рядом с волной, изображённой на рис. 3.1, но волна эта настолько протяжённая, что её начало и конец вам не видны. Тем не менее вы всё равно можете определить её скорость с помощью секундомера. Засеките время, когда мимо вас пройдёт положительный пик, и остановите отсчёт, когда с вами поравняется следующий положительный пик. Теперь у вас достаточно информации для определения скорости волны. Волна проходит расстояние d, равное одной длине волны, за время t. Это расстояние можно получить, умножив скорость на время: d=V∙t. (Если вы едете в автомобиле со скоростью V = 60 км/ч и ваша поездка занимает время t=1 час, то вы покроете расстояние d=60 км.) Если взять расстояние, равное одной длине волны, и разделить его на время, которое требуется на прохождение этого расстояния, то получится скорость: V=d/t. Наблюдение за проходящей мимо волной подобно наблюдению за движением очень длинного поезда. Вы видите, как один за другим следуют товарные вагоны. Если знать длину вагона и время, за которое он вагон проходит мимо вас, то можно определить скорость поезда.

Рис. 3.1. Волна, движущаяся в направлении x. Прямая представляет нулевую амплитуду волны. Волна испытывает положительные и отрицательные колебания относительно нуля. Расстояние между пиками — это длина волны. Волна движется вдоль оси x со скоростью V

Другая важная характеристика волн, связанная с их скоростью и длиной, — это частота. Учёные любят использовать греческие буквы для обозначения величин, поскольку латинские буквы в основном уже имеют общепринятое применение. Нет особых причин обозначать скорость буквой V, расстояние — d, а время — t, но обычно используются именно эти буквы^{4}. Поэтому мы обращаемся к греческому алфавиту. Обычно для обозначения длины волны используется буква λ (лямбда), а для частоты волны — ν (ню). Для понимания смысла частоты вновь рассмотрим идущий мимо товарный поезд. Если подсчитать, сколько вагонов проходит мимо за определённый отрезок времени, вы определите частоту вагонов. Если в минуту проходит 10 вагонов, то их частота составляет 10 в минуту, что часто записывается в виде 10 мин⁻¹. Частота волны определяется по числу циклов (пиков), отмечаемых в месте наблюдения за секунду. Если за секунду (сек) отмечено 1000 циклов, частота составляет ν=1000 сек⁻¹ = 1000 Гц. Для числа событий в секунду есть собственная единица — герц (Гц), названная в честь Густава Людвига Герца (1887–1975), который в 1925 году разделил с Джеймсом Франком Нобелевскую премию по физике

«за открытие законов соударения электрона с атомом».

Длина, скорость и частота волны связаны между собой уравнением λ∙ν=V.

Океанские волны

Когда волны распространяются по глубокой океанской воде, их гребни поднимаются выше среднего уровня моря, а впадины опускаются ниже. Типичная океанская волна имеет длину λ=160 м и движется со скоростью 60 км/ч. Период волны, то есть время между двумя её гребнями, составляет 10 сек, а частота, таким образом, равна ν=0,1 Гц. Амплитуда — это просто расстояние^{5} между гребнем и впадиной, так что зрительно представить себе амплитуду совсем несложно. (Волны разбиваются о берег, поскольку на мелкой воде их впадины доходят до дна и это их замедляет. Гребни движутся быстрее впадин и опрокидываются, отчего волна обрушивается на берег. У волн, движущихся в океане, гребни не обрушиваются.)

Звуковые волны

Звуковые волны — это волны плотности в воздухе. Стандартный камертон для ноты ля первой октавы имеет частоту 440 Гц. После удара его зубцы вибрируют с частотой 440 Гц. Эта вибрация порождает звуковые волны. Зубцы движутся взад и вперёд, «толкая» в соответствующих направлениях воздух с частотой 440 Гц и порождая волны с частотой ν=440 Гц. При температуре 21 °C скорость звука составляет 1239 км/ч, или 345 м/сек. Поскольку λ∙ν=V, длина звуковой волны с частотой 440 Гц составляет λ=0,78 м. Звуковые волны представляют собой чередование уплотнений воздуха выше средней плотности и разрежений воздуха ниже средней плотности, то есть воздуха становится то больше, то меньше. Плотность воздуха — это его масса, приходящаяся на единицу объёма, например число граммов в кубическом сантиметре (г/см³). Увеличение плотности обычно связано с ростом давления, так что можно представлять себе звуковые волны как волны давления, в которых давление воздуха возрастает и убывает с частотой 440 Гц. Когда звуковая волна достигает уха, периодические подъёмы и спады давления заставляют барабанную перепонку двигаться взад-вперёд с частотой звуковой волны, в данном случае равной 440 Гц. Движение барабанной перепонки передаёт звук во внутреннюю часть уха, где крошечные волоски покачиваются в соответствии с частотой звука. Движение этих волосков возбуждает нервы, а мозг расшифровывает нервные импульсы, и мы слышим звук.

Амплитуда звуковой волны — это разница между максимальной и минимальной плотностью (максимальным и минимальным давлением). В отличие от амплитуды океанских волн амплитуду звуковой волны увидеть нельзя, но, конечно, можно определить на слух разницу в амплитудах звуковых волн. Относительно просто превратить звуковые волны в электрические сигналы, что делается с помощью микрофона. Как только из звуковой волны получен электрический сигнал, её амплитуду можно узнать, измеряя величину электрического сигнала. Как и все классические волны, звуковые волны распространяются в определённом направлении и характеризуются амплитудой, длиной волны и скоростью.

Классические световые волны

Обсуждение океанских и звуковых волн подготовило нас к классическому волновому описанию света. В этом описании, которое во всех деталях определяется уравнениями Максвелла (Джеймс Клерк Максвелл, 1831–1879), свет представляется как электромагнитная волна. Эта волна обладает электрическим и магнитным полями, которые оба колеблются с одинаковой частотой. Если вы видели, как магнит притягивает небольшие предметы, то знакомы с действием магнитного поля. Магнитное поле магнита является статическим, а не колеблющимся, как в случае света. Вы также могли наблюдать проявления электрических полей. Если в очень сухой день причёсываться пластмассовой расчёской, то можно заметить, что волосы к ней притягиваются. К ней также могут прилипать оказавшиеся рядом маленькие кусочки бумаги. Эти эффекты обусловлены статическим электрическим полем. Электромагнитная волна состоит из электрического и магнитного полей, которые испытывают колебания.

В отличие от океанских волн, которые движутся по воде, и звуковых волн, которые распространяются в воздухе, световые волны могут распространяться в вакууме. Скорость света в вакууме обозначается буквой c и составляет c=3∙10⁸ м/сек. Скорость света примерно в миллион раз больше скорости звука. По этой причине при далёком грозовом разряде молния видна задолго до того, как слышен гром. Звуку требуется около трёх секунд, чтобы пройти километр. У света на это уходит около 0,000003 сек, или 3 мкс (микросекунды). Скорость света уменьшается, когда он движется в среде, отличной от вакуума. В воздухе свет имеет почти такую же скорость, как в вакууме, но в стекле она составляет лишь около двух третей c.

Что представляет собой электромагнитная волна, которая является классическим описанием света? В случае океанских волн колеблется уровень воды, который поднимается выше уровня моря или опускается ниже. В случае звуковой волны плотность воздуха (его давление) колеблется, поднимаясь выше или опускаясь ниже нормальных значений. Если взять небольшой объём, то количество воздуха (число молекул, составляющих воздух, — в основном кислорода и азота) становится больше или меньше среднего значения для воздуха, взятого в данном объёме. В электромагнитной волне колебания испытывают две сущности — электрическое поле и магнитное поле. Обычно говорят об электрическом поле, поскольку его легче измерить, чем магнитное. Колеблющееся электрическое поле — это электрическая волна.

Допустим, вы слушаете радио. Его антенна представляет собой отрезок провода, который детектирует радиоволны. Радиоволны — это просто низкочастотные электромагнитные волны. Это то же самое, что световые волны, но частота их значительно ниже. Электрическое поле в электромагнитной волне колеблется от максимального положительного значения амплитуды до максимального отрицательного значения. Металл радиоантенны содержит множество электронов, которые могут двигаться под действием электрического поля. (В дальнейшем нам предстоит подробный разговор об электронах, а электрическая проводимость будет обсуждаться в главе 19.) Колеблющееся электрическое поле радиоволны заставляет колебаться электроны в антенне. Электроника приёмника усиливает эти колебания электронов и превращает их в электрический сигнал, заставляющий аудиоколонки производить звуковые волны, которые мы слышим. Таким образом, в соответствии с классическими представлениями можно думать о свете как о колеблющихся электрическом и магнитном полях. Оба поля колеблются с одинаковой частотой и движутся вместе с одинаковой скоростью в одном направлении. Вот почему они называются электромагнитными волнами.

Видимый свет

При распространении света в вакууме выполняется соотношение λ∙ν=c. Видимые длины волн, то есть те, которые воспринимаются нашими глазами, лежат в диапазоне от 700 нм (красный) до 400 нм (синий). (Сокращение нм обозначает нанометр, то есть 10⁻⁹ метра, или 0,000000001 метра.) Длины волн видимого диапазона очень малы; скорость света очень велика, поэтому частоты этих волн очень велики. Частота ν красного света составляет 4,34∙10¹⁴ Гц, а синего света — 7,5∙10¹⁴ Гц (10¹⁴ — это сто триллионов). Эти значения сильно контрастируют с частотой звуковых волн (440 Гц) и океанских волн (0,1 Гц). Измерить амплитуду световых волн в отличие от океанских и звуковых волн довольно сложно.

Частота света настолько велика, что даже самая современная электроника не может различить их колебания. Вместо измерения амплитуды волны, определённой как амплитуда колебаний электрического поля, измеряется интенсивность света. Интенсивность I пропорциональна квадрату абсолютной величины электрического поля E, что записывается в виде I~|E|². Смысл абсолютной величины (обозначается двумя вертикальными линиями ||) состоит в том, что мы игнорируем знак величины — положительный или отрицательный — и делаем все значения положительными. Детектор света, такой как ПЗС-матрица в цифровой камере (ПЗС-матрица — это прибор с зарядовой связью, выдающий электрический сигнал, когда на него падает свет), измеряет количество света и его интенсивность, а не амплитуду световой волны. Глаза не измеряют непосредственно частоту световых волн в отличие от ушей, которые определяют частоту звуковых волн.

Сложение волн — интерференция

Волны одного типа, в том числе световые, могут складываться и порождать новые волны. Слева на рис. 3.2 показаны две одинаковые волны (с одинаковыми длиной и амплитудой, распространяющейся в одном направлении), которые находятся в фазе друг с другом. (Эти волны в действительности наложены друг на друга, но они смещены на рисунке так, чтобы можно было видеть их по отдельности.) «В фазе» означает, что положительные пики одной волны располагаются строго напротив положительных пиков другой волны, и, следовательно, отрицательные пики выровнены так же. Штриховая вертикальная линия на рисунке показывает, как выровнены эти пики. Когда волны находятся в фазе, говорят, что разность их фаз составляет 0° (ноль градусов). Один цикл волны соответствует фазе 360°. Начав с любой точки волны и пройдя вдоль неё 360°, вы попадёте в исходное положение, как если бы прошли 360° по окружности. Когда две одинаковые волны складываются в фазе, результирующая волна имеет удвоенную амплитуду. Это называется конструктивной интерференцией и показано в правой части рис. 3.2.

Волны, у которых сдвиг по фазе составляет 180°, тоже могут складываться друг с другом. Как показано в левой части рис. 3.3, у таких волн положительные пики верхней волны в точности совпадают с отрицательными пиками нижней волны, и наоборот^{6}. (И вновь подчеркнём: для того чтобы имела место интерференция, волны должны в действительности накладываться одна на другую, но на рисунке они сдвинуты по вертикали одна относительно другой, чтобы их можно было разглядеть.) Штриховая вертикальная линия на рисунке показывает, что положительный пик одной волны в точности выровнен относительно отрицательного пика другой. Когда две одинаковые волны, находящиеся в противофазе, складываются, положительные и отрицательные пики в точности гасят друг друга. Пусть, например, максимальное положительное значение — +1, а максимальное отрицательное значение составляет −1. Складывая +1 и −1, получаем ноль.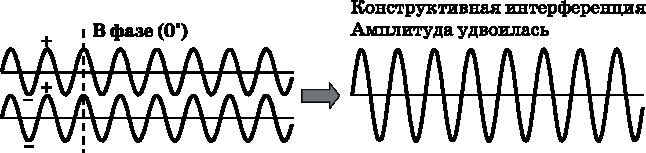

Рис. 3.2. Две одинаковые волны, находящиеся в фазе друг с другом. Эти волны испытывают положительные и отрицательные колебания относительно нуля (горизонтальная линия). Положительные пики выровнены друг относительно друга, как и отрицательные пики. Волны испытывают конструктивную интерференцию (складываются друг с другом) и порождают волну с удвоенной амплитудой

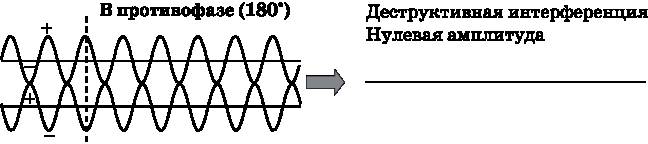Рис. 3.3. Две одинаковые волны, сдвинутые на 180° по фазе. Эти волны испытывают положительные и отрицательные колебания относительно нуля (горизонтальная линия). Положительные пики верхней волны строго выровнены с отрицательными пиками нижней волны, а отрицательные пики верхней волны строго выровнены с положительными пиками нижней волны. Волны испытывают деструктивную интерференцию, когда складываются друг с другом и дают нулевую амплитуду

На рис. 3.3 каждой точке верхней волны, имеющей положительное значение, строго соответствует точка нижней волны, имеющая такое же по абсолютной величине отрицательное значение, а каждой точке верхней волны, имеющей отрицательное значение, соответствует точка нижней волны, имеющая такое же по абсолютной величине положительное значение. Таким образом, волны в точности гасят друг друга, давая нулевую амплитуду, как показано в правой части рисунка. Это взаимное гашение называется деструктивной интерференцией.

Интерференционные картины и оптический интерферометр

Для интерференции волнам не обязательно строго накладываться друг на друга и идти в одном направлении. Они могут просто перекрываться в некоторой области пространства, и тогда интерференция происходит в этой области. Когда в 1980 году в Сан-Франциско открылся симфонический концертный зал Дэвиса, в нём обнаружились акустические проблемы. Хотя они оказались крайне сложными, нетрудно понять, как они возникли.

Представьте, что вы сидите в зале достаточно далеко от оркестра. Когда звучит ля первой октавы (440 Гц), акустические волны приходят прямо к вам, но они также отражаются от стен с обеих сторон от вас. При наличии отражения от стены справа от вас и отражения от стены слева от вас отражённые акустические (звуковые) волны от каждой стены приходят к вашему ряду кресел, скажем, под углом 30° и порождают вдоль него интерференционную картину. Будут места, где отражённые волны интерферируют конструктивно, делая звук громче, и места, где волны интерферируют деструктивно, делая звук тише. Интервалы между пиками и нулями интерференционной картины составляют 0,73 м (см. ниже формулу для интервалов). Таким образом, в зависимости от расположения вашего кресла ля первой октавы будет звучать громче или тише. Конечно, к вам приходит множество акустических волн разной частоты с разных направлений. Совокупность интерференционных эффектов искажает звук, который должен был приходить к вам прямо от оркестра. Проблемы в концертном зале Дэвиса были устранены в 1992 году путём установки 88 тщательно спроектированных панелей, свисающих с потолка вдоль двух боковых стен. Там нет двух одинаковых панелей. Они заполнены песком и весят 3850 кг. Эти панели мешают отражениям от стен доходить до аудитории.

Свет также может демонстрировать явление интерференции. Классическое представление об оптических интерференционных картинах позволяет объяснить экспериментальные результаты, которые мы сейчас рассмотрим. Однако, как будет показано в главах 4 и 5, классическое описание в итоге оказывается несостоятельным, когда в расчёт принимаются другие эксперименты. Для корректного описания потребуется ввести квантовомеханический принцип суперпозиции, что вновь приведёт нас к котам Шрёдингера.

Рис. 3.4. Входящая световая волна падает на полупрозрачное зеркало. Половина света проходит сквозь зеркало, а половина отражается от него. В каждом плече интерферометра свет отражается от стоящего в конце зеркала. Части каждого пучка сходятся под небольшим углом в области перекрытия. Справа от обведённой кружком области перекрытия в увеличенном масштабе в разрезе по x показано, что видно там при пересечении двух пучков. Именно в этом месте возникает интерференционная картина, в которой интенсивность периодически меняется вдоль оси x от максимального значения до нуля

На рис. 3.4 представлена схема интерферометра, использованного Майкельсоном (Альберт Абрахам Майкельсон, 1853–1931) в его исследованиях природы световых волн. Майкельсон получил в 1907 году Нобелевскую премию по физике

«за создание точных оптических инструментов, а также спектроскопические и метрологические исследования, выполненные с их помощью».

Майкельсон со своим коллегой Морли^{7} использовали интерферометр в попытке выяснить природу среды, в которой распространяются световые волны. Водяные волны движутся по воде. Звуковые волны — в воздухе. Эксперимент Майкельсона-Морли показал, что световые волны для своего распространения не нуждаются в среде, которую называли эфиром. Свет распространяется в вакууме. Не существует никакого эфира, заполняющего пространство. Световые волны, приходящие к нам от звёзд, не нуждаются в какой-либо среде, подобно океанским и звуковым волнам, которые представляют собой колебания воды и воздуха соответственно. Это был важный шаг в понимании того, что световые волны не являются волнами в том же самом смысле, что звуковые волны. Здесь же мы хотим лишь понять классическое описание того, что наблюдается с помощью интерферометра.

На рис. 3.4 луч света, рассматриваемый как световая волна, входит в прибор слева. Свет падает на полупрозрачное зеркало, расщепляющее пучок, которое отражает 50 % света и пропускает оставшиеся 50 %. При волновом описании света нетрудно направить часть волны одним путём, а часть — другим. Отражённый свет идёт вертикально в плоскости страницы, отражается от концевого зеркала 1, которое слегка наклонено так, чтобы отражённый луч не вернулся строго назад по первоначальному пути. Отражённый луч идёт вниз по странице и частично проходит сквозь зеркало-расщепитель. (Часть пучка отражается от расщепителя, но нас эта часть не интересует.) Данный маршрут представляет собой первое плечо интерферометра. 50 % исходного пучка проходит сквозь расщепитель и попадает на концевое зеркало 2, которое также наклонено под небольшим углом. Отразившись от него, луч вновь возвращается налево, почти повторяя свой первоначальный путь. Он отражается от расщепителя. (Часть, которая проходит сквозь расщепитель, нас не интересует.) Отражённая часть направляется вниз по странице. Этот маршрут представляет собой второе плечо интерферометра. В результате лучи, прошедшие один по первому плечу, а другой — по второму, сходятся вместе, пройдя одно и то же расстояние, и пересекаются под малым углом в «области перекрытия», которая обведена на рисунке кружком. Это наложение световых волн подобно наложению звуковых волн в симфоническом концертном зале Дэвиса, которое вызвало проблемы с интерференцией.

На рис. 3.4 световые лучи изображены прямыми линиями, но в любом реальном эксперименте лучи обладают некоторой шириной. Ось x на рисунке перпендикулярна биссектрисе угла (прямой, которая делит угол пополам), образованного пересекающимися лучами. Поскольку этот угол мал, ось x фактически перпендикулярна направлению распространения лучей и на данном рисунке имеет горизонтальное направление. На фрагменте, представленном в правой нижней части рисунка в увеличенном масштабе, показано, что видно вдоль оси x в области перекрытия. На графике по вертикальной оси отложена интенсивность света I, а по горизонтальной — положение вдоль оси x. Поскольку лучи пересекаются под небольшим углом, фазовое отношение между ними меняется вдоль оси x, и появляются чередующиеся области конструктивной и деструктивной интерференции. Интенсивность света меняется от максимального значения до нуля, снова до максимума и опять до нуля и так далее, и пересекающиеся световые волны порождают области конструктивной и деструктивной интерференции. Вблизи максимумов интенсивности световые волны приходят в фазе (0°, см. рис. 3.2) и складываются конструктивно, давая увеличение амплитуды. В точки нулевой интенсивности световые волны приходят со сдвигом по фазе на 180° (см. рис. 3.3) и складываются деструктивно — в точности гасят друг друга. Эту картину можно наблюдать, поместив в область перекрытия фотоплёнку или цифровую камеру и измерив интенсивность света в различных точках вдоль оси x.

При малом угле ширина интерференционных полос, то есть расстояние d между соседними пиками интенсивности или нулями, задаётся формулой d=λ∙θ, где λ — длина волны света, а θ — угол между пучками в радианах (1 радиан = 57,3°). Если используется красный свет с длиной волны 700 нм, а угол между пучками составляет 1°, то ширина интерференционных полос составит 40 мкм и на одном сантиметре их уместится 250. Такие полосы можно увидеть на плёнке или с помощью хорошей цифровой камеры. Если угол составит 0,1°, то интервал между полосами будет 0,4 мм, что можно увидеть невооружённым глазом. Если же угол будет 0,01° (это очень маленький угол), расстояние между интерференционными полосами составит 4 мм, то есть будет хорошо различимым. Чтобы получить такие 4-миллиметровые полосы, диаметр пересекающихся лучей должен быть намного больше 4 мм.

Как уже было сказано, в классическом представлении свет является электромагнитной волной, а его интенсивность пропорциональна квадрату амплитуды электрического поля (величины волны на рис. 3.1). В последующих рассуждениях мы не будем беспокоиться о единицах измерения. Задействовав множество констант, можно вывести все эти единицы, но этого не требуется для наших целей.

Пусть электрическое поле в пучке, прошедшем по одному из плеч интерферометра, имеет амплитуду 10. Тогда интенсивность составит 100 (10²=100=10∙10). Другой луч также имеет I=100. Это значения интенсивности в том случае, когда мы не наблюдаем лучи в области перекрытия. Когда лучи разделены, сумма значений их интенсивности составляет 200. Что происходит в области перекрытия? Волны интерферируют — конструктивно в одних местах и деструктивно в других (см. рис. 3.4, справа внизу). Таким образом, для определения значений интенсивности в области перекрытия необходимо сложить амплитуды электрических полей, а затем возвести результат в квадрат. В точках максимальной интенсивности в области перекрытия волны идеально совпадают по фазе и складываются конструктивно. Электрическое поле первого луча добавляется к электрическому полю второго луча: E=10+10=20. В таком случае интенсивность на пике интерференционной картины составляет I=E²=20²=400. Интенсивность составляет 400, что вдвое больше интенсивности простой суммы двух лучей самих по себе, когда они не испытывают конструктивной интерференции. В нулях интерференционной картины волны взаимодействуют идеально деструктивно. Электрическое поле +10 складывается с электрическим полем −10 и даёт ноль. Электрическое поле равно нулю, и I=0. Таким образом, интерференционная картина создаётся чередующимися областями конструктивной и деструктивной интерференции электромагнитных волн. В некоторых местах волны складываются, и мы видим пик. В других местах они вычитаются и дают ноль. Интерференция — это хорошо известное свойство волн, а картина, которую она даёт в интерферометре, — прекрасный пример волнового явления.

Интерферометр и интерференционную картину, изображённые на рис. 3.4, можно во всех подробностях описать в рамках классической электромагнитной теории. Детали интерференционной картины можно вычислить из уравнений Максвелла. Этот и многие другие эксперименты, включая передачу радиоволн, можно описать классической теорией. Поэтому классическая теория, которая рассматривает свет как волны, считалась корректной вплоть до начала XX века. Однако в главе 4 рассказывается, как эйнштейновское объяснение одного явления — фотоэлектрического эффекта — потребовало фундаментального переосмысления всего элегантного и, казалось бы, непогрешимого построения классической электромагнитной теории.

4. Фотоэлектрический эффект и объяснение Эйнштейна

В конце XIX века классическая электромагнитная теория была одним из величайших триумфов классической механики. Она могла объяснить результаты самых разнообразных экспериментальных наблюдений. Однако в начале XX века новые эксперименты создали серьёзные затруднения для классического волнового представления о свете, и прежде всего один эксперимент, который вместе со своим объяснением обнаружил фундаментальную проблему в, казалось бы, нерушимой волновой теории света.

Фотоэлектрический эффект

Эксперимент, о котором идёт речь, состоит в наблюдении фотоэлектрического эффекта. Суть его в том, что свет падает на поверхность металла и при определённых условиях из неё вылетают электроны. Здесь для нас электроны — это просто электрически заряженные частицы. Электрон заряжен отрицательно. (Далее мы узнаем, что электроны не являются в строгом смысле частицами по той же самой причине, по которой свет не является волнами.) Поскольку электроны — это заряженные частицы, их легко детектировать. Они могут порождать электрические сигналы в регистрирующей аппаратуре. На рис. 4.1 изображена схема фотоэлектрического эффекта, на которой входящий свет представлен как волна.

Рис. 4.1. Фотоэлектрический эффект. Свет падает на металл, и из него испускаются электроны (отрицательно заряженные частицы). В классическом представлении свет является волной, и взаимодействие этой волны с электронами в металле заставляет их вылетать

Можно измерить число электронов, выбитых из металла, и их скорость. Для конкретного металла и заданного цвета освещения, например голубого, оказывается, что электроны вылетают с определённой скоростью, а число вылетающих электронов зависит от интенсивности света. Если увеличить интенсивность, станет вылетать больше электронов, но каждый из них будет иметь всё ту же скорость, независимо от интенсивности освещения. Если цвет света изменить на красный, скорость электронов уменьшится, и чем больше света смещается по спектру в сторону красного цвета, тем меньше будет скорость электронов. При достаточно сильно покрасневшем свете электроны перестают вылетать из металла.

Волновая модель не работает

Проблема для классической теории, связанная с этими наблюдениями, состоит в том, что они совершенно несовместимы с волновым описанием света. Прежде всего, рассмотрим характер зависимости от интенсивности света. При волновом описании чем выше интенсивность света, тем больше амплитуда волны. Всякий, кто имел дело с морскими волнами, знает, что маленькие волны толкают слабо, а большие — сильно. Как показано на рис. 4.2, свет низкой интенсивности — это электромагнитная волна с малой амплитудой. Такая волна должна относительно слабо «толкать» электроны. И эти электроны должны вылетать из металла с относительно низкой скоростью. Напротив, свет высокой интенсивности ассоциируется с большой амплитудой волны. Такая волна должна сильно «толкать» электроны, и они должны вылетать из металла с высокой скоростью.

Рис. 4.2. Волновая картина зависимости фотоэлектрического эффекта от интенсивности света. Свет низкой интенсивности имеет малую амплитуду волны. Поэтому волна должна относительно слабо «толкать» электроны, и они будут вылетать из металла с низкой скоростью. Свет высокой интенсивности имеет большую амплитуду волны. Большая волна должна сильно «толкать» электроны, и они будут вылетать из металла с высокой скоростью

Доведём дело до полной ясности. Световая волна связана с колеблющимся электрическим полем. Электрическое поле меняется от положительного к отрицательному, снова к положительному и опять к отрицательному с частотой, соответствующей свету. Электрон в металле тянет в одном направлении, когда поле положительно, и тащит в другом направлении, когда поле отрицательно. Эти колебания электрического поля толкают электрон взад и вперёд. Согласно классической теории, если волна имеет достаточную амплитуду, она выбивает электрон из металла. Если амплитуда волны больше (интенсивность выше), она толкает электрон сильнее, и он должен вылететь из металла с более высокой скоростью. Однако наблюдается вовсе не это. Когда интенсивность света увеличивается, электроны вылетают из металла с той же самой скоростью, но при этом выбивается больше электронов.

Более того, когда свет смещается по цвету в сторону красного (то есть в сторону более длинных волн), электроны вылетают из металла с меньшей скоростью независимо от интенсивности. Хотя в волновой модели более длинноволновый свет менее энергичен, должна быть возможность, подняв интенсивность света, увеличить амплитуду волны и тем самым повысить скорость электронов, вылетающих из металла. Однако, как и с более голубыми волнами, повышение интенсивности увеличивает лишь число электронов, вылетающих из металла, но при заданном цвете (длине волны) все они вылетают с одинаковой скоростью.

Дополнительная проблема состоит в том, что, если свет достаточно сильно сместить в красную сторону спектра, электроны вообще перестают вылетать. Электроны обладают некоторой энергией связи с металлом, поскольку отрицательно заряженные электроны притягиваются к положительно заряженным ядрам атомов металла. (Атомы подробно обсуждаются, начиная с главы 9, а металлы — в главе 19.) Именно энергия связи удерживает электроны от вылетания из металла в отсутствие света. Согласно волновой картине, всегда должна быть возможность настолько поднять интенсивность света, сделав тем самым амплитуду колебаний электрического поля достаточно большой, чтобы превзойти энергию связи. Если вы стоите в полосе прибоя, то маленькая волна не собьёт вас с ног, но если волны становятся всё больше и больше, то в конце концов они окажутся достаточно велики для того, чтобы нарушить связь ваших ног с дном, заставив вас плыть. Однако в случае света, который достаточно сильно смещён в красную сторону, как бы ни была велика волна — связь электронов с металлом преодолеть невозможно.

Эйнштейн даёт объяснение

Итог этих экспериментальных наблюдений состоит в том, что волновая модель света, которая так хорошо описывает интерференционную картину на рис. 3.4, не даёт приемлемого описания фотоэлектрического эффекта. Его объяснение было дано в 1905 году Эйнштейном (Альберт Эйнштейн, 1879–1955). В 1921 году он получил Нобелевскую премию по физике

«за заслуги перед теоретической физикой, и в особенности за объяснение закона фотоэлектрического эффекта».

Может показаться удивительным, что Эйнштейн, известный своей теорией относительности, получил Нобелевскую премию за объяснение фотоэлектрического эффекта. Однако это был важный шаг в переходе от классической теории к квантовой. Премия Эйнштейна демонстрирует важность объяснения фотоэлектрического эффекта для современной физики.

Эйнштейн заявил, что свет состоит не из волн, а из фотонов, или квантов света. В случае фотоэлектрического эффекта фотон ведёт себя скорее как частица, чем как волна. По утверждению Эйнштейна, поток света состоит из множества фотонов, каждый из которых является дискретной частицей. (Как подробно обсуждается далее, это не частицы в классическом понимании данного слова.) На рис. 4.3 показано, как один фотон «толкает» электрон и выбивает его из металла. Этот процесс в чём-то похож на то, как биток в бильярдной игре «пул» ударяет по неподвижному прицельному шару и отправляет его через весь стол. Ударяя по нему, биток передаёт ему энергию в кинетической форме, то есть в виде энергии движения. Столкновение приводит к тому, что биток энергию теряет, а шар, по которому он попал, приобретает. Световой луч состоит из множества фотонов, но один фотон выбивает из металла один электрон.

Рис. 4.3. Эйнштейн представил свет состоящим из дискретных квантов — «частиц» света, называемых фотонами. При фотоэлектрическом эффекте один фотон толкает один электрон и выбивает его из металла

Чем выше интенсивность света, тем больше фотонов содержит луч. Как показано на рис. 4.4, чем больше фотонов падает на металл, тем больше они выбивают из него электронов. Поскольку один фотон бьёт по одному электрону, увеличение интенсивности светового пучка не приводит к изменению скорости испускаемых электронов. В пуле скорость прицельного шара зависит от того, как быстро двигался биток. Представьте себе два битка, которые одновременно с одинаковой скоростью ударяют по двум разным прицельным шарам. После удара оба прицельных шара будут двигаться с одинаковой скоростью. При увеличении числа фотонов определённого цвета, падающих на металл, из него выбивается больше электронов, но все они имеют одинаковую скорость. В отличие от волновой модели, увеличение интенсивности не приводит к усилению толчка, получаемого электроном, оно связано лишь с ростом числа фотонов, выбивающих соответственно больше электронов. Все фотоны, независимо от их количества, бьют по электронам с одной и той же силой. Поэтому электроны вылетают с одинаковой скоростью независимо от интенсивности света.

Рис. 4.4. Повышение интенсивности светового луча соответствует увеличению числа составляющих его фотонов. Большее число фотонов может толкнуть и выбить из металла больше электронов, так что повышение интенсивности приводит к росту числа электронов, вылетающих из металла

Красный свет выбивает более медленные электроны, чем голубой

Для того чтобы объяснить, почему смещение цвета в красную сторону (к более длинным волнам и меньшей энергии) приводит к уменьшению скорости вылетающих электронов, Эйнштейн использовал формулу, предложенную Планком (Макс Карл Эрнст Людвиг Планк, 1858–1947). Планк первым выдвинул идею о том, что энергия испускается дискретными порциями — квантами, когда объяснял другое связанное со светом явление, называемое излучением чёрного тела. Когда, например, кусок металла нагревается до высокой температуры, он начинает светиться. Так, нагревательный элемент электрокамина или калорифера светится красным. Если температура повышается, свет смещается в голубую сторону. Это относится не только к кускам металла, но также и к звёздам. Красные звёзды — относительно холодные. Жёлтые звёзды, такие как наше Солнце, — горячие. Голубые звёзды — очень горячие. В 1900 году классическая физика не могла объяснить количество света каждого цвета, испускаемого горячим объектом. Планк нашёл объяснение, которое актуально и поныне, введя новое представление о том, что электроны в металле могут «осциллировать»^{8} только с определёнными дискретными частотами. Энергетические ступени между этими частотами называются квантами. В 1918 году Планк получил Нобелевскую премию по физике

«в знак признания услуг, которые он оказал физике своим открытием квантов энергии».

От квантов энергии, открытых Планком, происходит название квантовой механики.

В своей работе Планк ввёл формулу, которая связывает частоту электрона с его энергией: E=h∙ν. В этой формуле ν — частота, обсуждавшаяся в главе 3, а h называется постоянной Планка. Её значение h=6,6∙10⁻³⁴ Дж∙сек, где Дж — единица энергии джоуль, а сек — секунды. В этой формуле ν измеряется в герцах (Гц), то есть в обратных секундах (1/сек); поэтому результат умножения h на ν измеряется в единицах энергии — джоулях. В своём описании излучения чёрного тела Планк постулировал, что энергия может изменяться только дискретными шагами. Она может быть равна h∙ν, 2h∙ν, 3h∙ν и т. д., но не может принимать промежуточные значения между этими ступенями. Понимание того, что на атомном уровне энергия меняется дискретными квантами, положило начало квантовой механике.

Эйнштейн предположил, что формула Планка также применима и к фотонам, так что энергия фотона зависит от его частоты ν: E=h∙ν. С помощью этой формулы Эйнштейн объяснил, почему красный свет порождает более медленные электроны, чем голубой. Частота красного света ниже, чем голубого. Поэтому красный фотон менее энергичен, чем голубой. Продолжая аналогию с пулом, мы понимаем, что голубой фотон сильнее толкает электрон, чем красный, и поэтому электрон приобретает более высокую скорость. При таком объяснении становится понятно, почему по мере покраснения света выбиваемые им из металла электроны становятся всё медленнее.

Очень красный свет не выбивает электронов

Остаётся объяснить ещё одно наблюдение: почему электроны перестают вылетать из металла, когда свет становится слишком красным? Эйнштейн ответил и на этот вопрос. Когда электрон выбивается из металла фотоном, у него имеется определённая кинетическая энергия. Кинетическая энергия связана с его движением. Чем выше эта энергия, тем быстрее движется электрон. Она обозначается E_k, где индекс k означает «кинетическая». Кинетическая энергия вычисляется по формуле

E_k=½m∙V²,

где m — масса, а V — скорость. В таком случае скорость электрона, вылетевшего из металла, связана с его энергией, которая в свою очередь связана с энергией выбившего его фотона. Более энергичный фотон передаст электрону больше кинетической энергии, и электрон будет двигаться быстрее (с большей скоростью V).

Как уже говорилось, электроны удерживаются в металле энергией связи, обозначаемой E_b, где индекс b означает «связывание» (binding). В связи с этим часть энергии, принесённой фотоном, уходит на преодоление энергии связи. Кинетическая энергия, с которой электрон выходит из металла, равна разности энергии фотона E=h∙ν и энергии связи E_b. Таким образом, кинетическая энергия электрона составляет E_k=h∙ν−E_b. Чтобы электрон вылетел из металла, энергия фотона h∙ν должна быть больше энергии связи E_b. По мере того как свет краснеет (длина волны λ увеличивается), частота ν уменьшается, поскольку ν=с/λ, где c — скорость света. При некотором достаточно красном цвете h∙ν становится меньше E_b, и электроны больше не могут вылетать из металла. Повышение интенсивности света увеличивает число фотонов, падающих на металл, но ни один из них не имеет достаточной энергии, чтобы выбить электрон.

Тот факт, что электроны перестают вылетать из металла, когда фотоны уходят достаточно далеко в красную область (имеют достаточно низкую энергию), можно понять на примере детской уличной игры Red Rover^{9}. В этой игре группа детей из одной команды растягивается в шеренгу, держась за руки. Игрок из другой команды с разбегу бросается на эту шеренгу и, если бежит достаточно быстро (имеет высокую энергию), разрывает её и продолжает двигаться, хотя и медленнее. При несколько меньшей скорости он всё ещё сможетпрорвать шеренгу. Однако если он будет бежать достаточно медленно, то не сможет пробиться сквозь неё, поскольку энергии не хватит, чтобы преодолеть энергию связи рук в шеренге.

С какой скоростью вылетает электрон

Интересно прикинуть, с какой скоростью движется электрон, когда он вылетает из куска металла. Разные металлы имеют разную энергию связи, называемую работой выхода. Энергию связи металлов можно определить, смещая свет всё дальше в красную область и наблюдая, при какой длине волны фотоны не смогут выбивать электроны. Для металлов с небольшой энергией связи предельная длина волны для выбивания электронов обычно составляет около 800 нм. Для λ=800 нм: ν=3,75∙10¹⁴ Гц и E_b=h∙ν=2,48∙10⁻¹⁹ Дж. Если светить на такой металл зелёным светом с длиной волны 525 нм, то энергия фотона составит 3,77∙10⁻¹⁹ Дж. Кинетическая энергия выбитого из металла электрона будет E_k=h∙ν−E_b=1,30∙10⁻¹⁹ Дж. Нетрудно найти скорость движения электрона из уравнения

E_k=½m_e∙V²=1,30∙10⁻¹⁹ Дж,

где m_e — масса электрона, составляющая 9,11∙10⁻³¹ кг. Умножая уравнение для E_k на 2 и деля его на m_e, получаем:

V²=2∙(1,30∙10⁻¹⁹ Дж)/m_e = (2,60∙10⁻¹⁹Дж)/(9,11∙10⁻³¹кг) = 2,85∙10¹¹ м²/сек².

Это значение квадрата скорости. Извлекая квадратный корень, получаем: V=5,34∙10⁵ м/сек, что составляет около двух миллионов километров в час. В этом примере фотоэлектрического эффекта выбитый электрон движется весьма резво.

Классическая электромагнитная теория, описывающая свет как волны, прекрасно работает применительно к огромному числу явлений, включая интерференцию, но совершенно не подходит для объяснения фотоэлектрического эффекта. Эйнштейн объяснил фотоэлектрический эффект, но теперь свет не может быть волнами. Что же тогда происходит с классическим описанием интерференции? Для примирения фотоэлектрического эффекта и интерференции нам придётся вернуться к квантовой теории и котам Шрёдингера.

5. Свет: волны или частицы?

Объяснение фотоэлектрического эффекта, которое обсуждалось в главе 4, требует нового теоретического описания интерференционного эксперимента, изображённого на рис. 3.4. Для того чтобы объяснение этого эксперимента не противоречило описанию фотоэлектрического эффекта, надо отказаться от классического мышления и совершить большой скачок к мышлению квантовомеханическому. Обсуждая в главе 2 абсолютные размеры, мы говорили о том, что измерению малой в абсолютном смысле системы всегда сопутствует возмущение, которым нельзя пренебречь. Однако мы не обсуждали природу и следствия такого возмущения. Теперь пришло время вплотную заняться выяснением истинного характера материи и тем, что происходит, когда мы выполняем измерения.

Проблема, с которой мы столкнулись, состоит в том, что для объяснения явления интерференции на рис. 3.4 используются световые волны, а для объяснения фотоэлектрического эффекта, представленного на рис. 4.3 и 4.4, — «частицы света» — кванты, называемые фотонами. В классической модели световых волн для количественного описания интерференции используются уравнения Максвелла. В этой теории световая волна математически описывается волновой функцией. Функция задаёт её амплитуду, частоту и пространственную локализацию. Входящая световая волна характеризуется одной волновой функцией. В классическом представлении после того как световая волна попадает на полупрозрачное расщепляющее зеркало, половина волны уходит по одному плечу интерферометра, а половина — по другому (см. рис. 3.4). Теперь есть две волны и две волновые функции — по одной для каждой волны. Эти волновые функции описывают волны, которые вдвое уступают по интенсивности первоначальной входящий волне и имеют разную локализацию — в двух плечах интерферометра. Если эти две волновые функции математически объединить для описания того, что происходит в области перекрытия, обведённой кружком на рис. 3.4, то можно рассчитать интерференционную картину. Всё это так хорошо работает, что считалось, будто то же самое математическое представление может быть применимо и к фотонам.

Классическое описание интерференции не годится для фотонов

На рис. 5.1 вновь изображён интерферометр. Он точно такой же, как на рис. 3.4, за исключением того, что световой луч на этот раз состоит из фотонов. Первоначально считалось, что когда луч из фотонов падает на полупрозрачное зеркало, половина фотонов движется по первому плечу прибора и попадает на концевое зеркало 1, а другая половина идёт по второму плечу интерферометра, попадая на концевое зеркало 2. Затем фотоны отражаются от концевых зеркал, и после ещё одного попадания на полупрозрачное зеркало половина фотонов из каждого плеча достигает области перекрытия. Считалось, что интерференционная картина возникает тогда, когда фотоны из одного плеча прибора интерферируют с фотонами из другого плеча. Это представление, как выяснилось, является ошибочным.

В отношении описания эффекта интерференции математическая формулировка, основанная на максвелловских волновых функциях, совершенно не изменилась. Однако физический смысл волновой функции был пересмотрен. Вместо амплитуды электромагнитной волны в определённой области пространства, например в первом или втором плече интерферометра, волновая функция была переопределена как описание числа фотонов в некоторой области пространства. Прежде считалось, что волновая функция даёт нам амплитуду волны в некоторой области пространства, а по этой амплитуде можно вычислить интенсивность. После переопределения стало считаться, что волновая функция говорит, сколько фотонов находится в области пространства, скажем в первом плече интерферометра, и интенсивность по-прежнему можно вычислить. Такое переопределение кажется совершенно разумным, но оно ошибочно! Само представление о том, что по каждому плечу интерферометра движется половина фотонов, является глубоким заблуждением. Для корректного описания необходимо совершить скачок к квантовомеханическому мышлению.

Рис. 5.1. Луч света состоит из фотонов, которые падают на полупрозрачное зеркало. В первоначальном ошибочном описании явления интерференции в терминах фотонов считалось, что половина фотонов проходит в каждое плечо интерферометра. Фотоны из каждого плеча попадают затем в область перекрытия, где якобы фотоны из одного плеча интерферируют с фотонами из другого плеча, порождая интерференционную картину. Мысль о том, что фотоны из одного плеча интерферируют с фотонами из другого плеча, является ошибочной

В картине, где половина фотонов движется по каждому плечу интерферометра, а затем эти половины сходятся и интерферируют между собой, много ошибочного. Простейший эксперимент, выявляющий проблему в таком описании, — это анализ зависимости интерференционной картины (см. увеличенный фрагмент на рис. 5.1 внизу справа) от интенсивности. Форма наблюдаемой интерференционной картины в области перекрытия интерферометра не зависит от интенсивности света, который послужил для её создания. При выбранном методе регистрации (фотоплёнка или цифровая камера) увеличение интенсивности сокращает время, требуемое для получения качественного изображения, но рисунок на нём остаётся неизменным. Таким образом, интервалы между пиками и нулями интерференционной картины, а также их форма остаются без изменений.

Как говорилось в главе 3, периодичность рисунка зависит от угла пересечения лучей и от длины волны света. Она не зависит от интенсивности. Если повысить интенсивность, потребуется больше времени, чтобы картина прорисовалась, но сам узор не изменится по форме. Стандартная красная лазерная указка даёт мощность 1 мВт (милливатт), то есть одну тысячную ватта, или 0,001 Дж/сек (джоуль в секунду). Красный свет имеет длину волны около λ=650 нм. Пользуясь формулами λ∙ν=c и E=h∙ν, где h — постоянная Планка, ν — частота света, а c — скорость света, можно найти, что один фотон с длиной волны 650 нм несёт энергию около 3∙10⁻¹⁹ Дж. Таким образом, лазерная указка мощностью 1 мВт испускает около 3∙10¹⁵ (трёх тысяч триллионов) фотонов в секунду. Если использовать их как входящий пучок интерферометра, то зарегистрировать интерференционную картину будет очень просто, даже если интервал между её максимумами достаточно велик (см. обсуждение этого интервала в главе 3 после рис. 3.4), и вы даже сможете увидеть интерференционную картину своими глазами.

Представьте себе, что интенсивность света начинает постепенно уменьшаться. Вскоре вы уже не сможете разглядеть интерференционную картину, поскольку глаз — не очень чувствительный детектор света, но её по-прежнему можно зарегистрировать на фотоплёнку или с помощью цифровой камеры. Зафиксированный узор при этом останется неизменным. Если уменьшить интенсивность в 3000 раз — до триллиона фотонов в секунду, — рисунок останется прежним. В описании, согласно которому половина фотонов следует по одному плечу интерферометра, а другая половина — по второму, полтриллиона фотонов пойдёт по первому плечу и полтриллиона — по второму. Понизьте интенсивность до миллиарда фотонов в секунду — узор останется тем же. Дальнейшее уменьшение интенсивности до миллиона фотонов в секунду также ничего не меняет. И вот тут ошибочность описания становится очевидной. Снизьте интенсивность света так, чтобы лишь один фотон в секунду входил в прибор, — изображение вновь не изменится. С одним фотоном в секунду потребуется долгое время накапливать сигнал, чтобы увидеть интерференционную картину, но если набраться терпения и подождать, рисунок будет тот же самый.

Когда в интерферометр входит всего один фотон в секунду, внутри прибора находится лишь один фотон. Ему требуется порядка одной стомиллионной доли секунды (10⁻⁸ сек), чтобы пройти через интерферометр. При интенсивности света один фотон в секунду нет фактически ни единого шанса обнаружить внутри инструмента более одного фотона за раз, и тем не менее если получить интерференционную картину, она окажется в точности такой же. Однако модифицированное классическое описание эффекта интерференции в терминах фотонов говорит, что половина фотонов идёт по первому плечу прибора, а половина — по второму. Фотоны из первого плеча интерферируют с фотонами из второго плеча и порождают интерференционную картину. Если в каждый момент времени внутри прибора имеется лишь один фотон, то там нет другого фотона, с которым он мог бы интерферировать. Модель, согласно которой по каждому плечу прибора идёт половина фотонов, предсказывает, что интерференционная картина должна исчезать при достаточно низкой интенсивности света. Но она не исчезает. Данная модель ошибочна!

Новое описание фотонов в интерферометре

Вот здесь-то и требуется полное изменение мышления, возвращающее нас к котам Шрёдингера. Как может возникать интерференционная картина, если в каждый момент в интерферометр входит лишь один фотон? Наше понимание этой проблемы и природы квантовой механики в целом основывается на концептуальной интерпретации математического формализма, тесно связанного с работой Макса Борна (1882–1970). Борн получил Нобелевскую премию по физике в 1954 году

«за фундаментальные исследования по квантовой механике, в особенности за статистическую интерпретацию волновой функции».

Эту интерпретацию часто называют копенгагенской.

Корректное описание эксперимента с интерферометром состоит в том, что каждый фотон движется по обоим плечам интерферометра. Это и есть наш большой скачок. Одиночный фотон встречает полупрозрачное зеркало. Значит, с 50-процентной вероятностью фотон отразится и пойдёт по первому плечу интерферометра (см. рис. 5.1), а с 50-процентной вероятностью — по второму плечу. Это ошибка. Когда фотон встречает зеркало — разделитель пучка, — его состояние меняется. Если фотон действительно движется по первому плечу, назовём это состояние движения «трансляционным состоянием 1», сокращённо T₁. Если фотон движется по второму плечу, назовём это состояние движения «трансляционным состоянием 2», сокращённо T₂. После взаимодействия фотона с разделителем пучка он не находится ни в состоянии T₁, ни в состоянии T₂. Состояние системы после разделителя пучка называют состоянием суперпозиции. Это смесь состояний T₁ и T₂ в равных пропорциях. В некотором смысле фотон одновременно находится в состояниях T₁ и T₂. Это звучит по-настоящему странно. Одиночный фотон находится в двух областях пространства одновременно. Он пребывает в трансляционном состоянии T=T₁+T₂ — суперпозиции, в которой поровну смешаны состояния T₁ и T₂.

Фотон находится в этой суперпозиции трансляционных состояний T=T₁+T₂, поскольку именно это о нём известно. Он с 50-процентной вероятностью находится в первом плече (T₁) и с 50-процентной вероятностью — во втором (T₂). Борновская интерпретация волновой функции заключается в том, что это не реальная волна в смысле амплитуды колеблющегося электромагнитного поля. Правильнее говорить, что волновая функция описывает «амплитуду вероятности волны». Ошибочная интерпретация волновой функции в терминах фотонов состоит в том, что она якобы говорит, сколько фотонов находится в каждом плече прибора, то есть сколько фотонов пребывает в некоторой области пространства. Правильная интерпретация состоит в том, что волновая функция фотона говорит о вероятности обнаружения фотона в этой области пространства.

Может показаться, что различие между ошибочной и правильной интерпретациями незначительно, однако, как подробно объясняется далее, оно фундаментально меняет наше представления о природе. В классическом описании света его интенсивность пропорциональна абсолютному значению квадрата амплитуды электрического поля, которая, в свою очередь, задаётся амплитудой волновой функции. В борновской интерпретации возведённая в квадрат абсолютная величина волновой функции для определённой области пространства даёт вероятность обнаружения частицы, в нашем случае фотона, в этой области пространства.

Фотон интерферирует сам с собой

При попадании фотона на разделитель пучка рождаются две волны амплитуды вероятности: одна в первом плече, другая — во втором. В целом волна амплитуды вероятности T является суперпозицией волн амплитуды вероятности T₁ и T₂. Встретившись с разделителем, каждый отдельный фотон попадает в состояние T₁+T₂. Поскольку за разделителем есть две волны амплитуды вероятности, они пересекаются в области перекрытия. С одиночным фотоном внутри интерферометра связаны две волны — T₁ и T₂. Интерференция этих двух волн определяет высокую вероятность обнаружить фотон вблизи пика интерференционной картины и низкую вероятность обнаружить фотон вблизи её нуля. Фотон интерферирует сам с собой, поскольку в интерферометре он состоит из двух волн, и эти две волны могут интерферировать друг с другом. Так как после прохождения разделителя пучка каждый отдельный фотон попадает в состояние суперпозиции T₁+T₂, снимается проблема, связанная с низкой интенсивностью света. Одиночный фотон, входя в прибор, порождает две волновые функции, две волны амплитуды вероятности в интерферометре. Поэтому всегда есть пара волн, порождающих интерференционную картину.

Фотон может находиться в двух местах сразу

Первая естественная реакция человека с классическим мышлением на борновскую интерпретацию: «Это безумие какое-то!» Мы что, действительно верим, будто один фотон может находиться в двух местах сразу? После разделителя пучка порождается состояние T₁+T₂. Это состояние означает, что в некотором смысле фотон одновременно находится в обоих плечах прибора. Если поместить детектор в плечо 1, чтобы посмотреть, сколько там света, то обнаружится, что туда прошла половина света. Однако это не та информация, которая нам нужна. Возможно, половина фотонов пошла по каждому плечу, и мы видим эту половину, или, возможно, имеется 50-процентная вероятность того, что каждый фотон прошёл в каждое плечо. В этом случае мы тоже увидим половинную интенсивность. Правильный эксперимент состоит в использовании настолько слабого света, что в каждый момент внутри прибора находится лишь один фотон.

Рассмотрим эксперимент, в котором интерферометр обстреливается одиночными фотонами. Будем использовать фотодетектор, настолько чувствительный, что он способен зарегистрировать отдельный фотон. Это легко достижимо с помощью научного эквивалента цифровой суперкамеры. Поместим детектор в первое плечо интерферометра. Фотон входит в прибор, и мы регистрируем его. Мы наблюдаем фотон целиком, а не его половину. Другой фотон входит в прибор, но мы его не видим. Пять фотонов входит в прибор. Мы регистрируем два из них, а остальные три не замечаем. Продолжая в том же духе достаточно долго, мы обнаруживаем, что детектор в левом плече прибора регистрирует 50 % фотонов. Мы также видим, что никакой интерференционной картины не возникает. Фактически наблюдается одно светлое пятно (без периодически меняющегося рисунка) в той области, где раньше возникала интерференционная картина.

Наблюдение вызывает непренебрежимо малое возмущение, приводящее к изменению состояния

Что же происходит? Попадая на разделитель пучка, фотон оказывается в состоянии суперпозиции T₁+T₂. Однако фотоны — это частицы, малые в абсолютном смысле. Акт их наблюдения вызывает непренебрежимо малое возмущение. Помещая фотодетектор в первое плечо прибора, мы производим наблюдение местоположения фотона. Этот акт наблюдения заставляет систему перескочить из состояния суперпозиции T₁+T₂ в одно из чистых состояний — либо T₁, либо T₂. Волновая функция суперпозиции «коллапсирует» в одно из чистых состояний, из которых складывается эта суперпозиция. Если система перескакивает в состояние T₁, то фотон регистрируется. И конечно, попав в фотодетектор, он уже не распространяется дальше по интерферометру. Если фотон перескакивает в состояние T₂, он не регистрируется фотодетектором, расположенным в первом плече, и продолжает двигаться дальше, достигая в конце концов области, подготовленной к регистрации интерференционной картины. Однако, поскольку этот фотон находится в чистом состоянии T₂, то имеется лишь одна волна амплитуды вероятности. Когда она достигает области «перекрытия» (на рис. 5.1 внизу), там нет другой волны амплитуды вероятности, с которой могла бы возникнуть интерференция. Поэтому никакой интерференционной картины не появляется. Одиночное пятно образуется, когда каждый фотон, пройдя через прибор в чистом состоянии T₂, подобно пуле, попадает в это пятно на детекторе. Размер пятна такой же, как размер (диаметр) исходного светового пучка, вошедшего в прибор, и в нём нет пространственных колебаний, характерных для интерференционной картины.

Возвращаемся к котам Шрёдингера

Наблюдение местоположения фотона с помощью фотодетектора в первом плече интерферометра заставляет фотон перескочить из состояния суперпозиции T₁+T₂ в чистое состояние — либо T₁, либо T₂. Однако единственное измерение не позволяет узнать, какое состояние будет получено в результате наблюдения. Шансы получить T₁ или T₂ составляют 50 на 50. После многочисленных измерений мы знаем, что вероятность перескакивания в состояние T₁ равна 50 %, но невозможно заранее сказать, что случится в конкретном единичном наблюдении. Это настоящее физическое проявление ситуации, которую мы обсуждали в главе 1 на примере котов Шрёдингера, когда в каждом из 1000 ящиков было по коту. Каждый кот находился в состоянии суперпозиции — на 50 % живой и на 50 % мёртвый. В этом совершенно нефизическом, но способствующем пониманию сути вопроса сценарии при вскрытии ящика выполнялось наблюдение состояния здоровья кота. Иногда он оказывался совершенно здоровым, иногда — мёртвым. После вскрытия всех ящиков было определено, что вероятность обнаружить живого кота составляет 50 %, но нет способа предсказать до вскрытия конкретного ящика, то есть до выполнения отдельного наблюдения, живой или мёртвый кот будет там найден. До вскрытия ящика кот находится в состоянии суперпозиции живого и мёртвого в пропорции 50:50. Акт выполнения наблюдения порождает непренебрежимое возмущение и заставляет состояние суперпозиции перескочить в одно из чистых состояний — либо живое, либо мёртвое. Как говорилось в главе 1, состояние суперпозиции живого/мёртвого кота не существует и не может существовать, но интерферометр — это реальный пример той идеи, иллюстрацией которой служат коты Шрёдингера.

С помощью полупрозрачного зеркала фотон легко привести в состояние суперпозиции, представляющее собой смесь 50 на 50 двух трансляционных состояний. Когда фотон находится в состоянии суперпозиции, невозможно сказать, движется он по первому или по второму плечу прибора. Можно лишь сказать, что если мы выполним измерение, чтобы узнать, где фотон находится, это вызовет возмущение, которым невозможно пренебречь. Данное возмущение приведёт к тому, что состояние системы изменится, и, вместо того чтобы быть в обоих плечах интерферометра с равной вероятностью, фотон окажется либо в одном из них, либо в другом. Интерференционная картина рождается, когда волны амплитуды вероятности фотона интерферируют друг с другом. Две компоненты состояния суперпозиции — T₁ и T₂, из которых складывается совокупная волна амплитуды вероятности для фотона в приборе, — интерферируют друг с другом. Если выполняется наблюдение, позволяющее узнать, где находится фотон, он будет найден либо в первом, либо во втором плече интерферометра. Однако сам факт наблюдения меняет систему так, что она более не находится в состоянии суперпозиции. Амплитуда вероятности больше не состоит из двух частей, которые могут интерферировать друг с другом, и интерференционная картина исчезает. Таким образом, фотон в интерферометре — это реальное проявление идей, связанных с котами Шрёдингера.

Возвращаемся к фотоэлектрическому эффекту

В главе 4 фотоэлектрический эффект описывается в терминах фотонов, которые являются частицами, ведущими себя в некотором смысле наподобие световых пуль. Один фотон ударяет по одному электрону и выбивает его из куска металла (см. рис. 4.3). Это описание фотоэлектрического эффекта показывает, что классическое представление о свете как об электромагнитных волнах неверно. Для того чтобы объяснить фотоэлектрический эффект и одновременно тот факт, что фотоны порождают интерференционную картину, потребовалось ввести новую концепцию. Борновская интерпретация волновой функции как волны амплитуды вероятности придаёт фотону необходимые волноподобные характеристики, так что фотоны способны порождать интерференционную картину. Однако при обсуждении волн амплитуды вероятности в применении к интерферометру мы характеризовали положение фотона лишь с точностью до выбора одной из двух больших областей пространства; фотон находился в состоянии суперпозиции T₁+T₂ с равной вероятностью оказаться в первом или во втором плече интерферометра.

Фотоэлектрический эффект предполагает, что фотон весьма мал. В главе 6 будет показано, как суперпозиция волн амплитуды вероятности может породить фотон, имеющий очень маленькие размеры. Эти идеи приведут нас к центральному и самому неклассическому аспекту квантовой механики — принципу неопределённости Гейзенберга.

6. Размеры фотона и принцип неопределённости Гейзенберга

В главе 5 мы узнали, что фотон в интерферометре интерферирует сам с собой. Фотон в некотором смысле может находиться более чем в одном месте сразу. Положение фотона описывается волной амплитуды вероятности. Она не похожа на водяную, звуковую или даже классическую электромагнитную волну. Волна, ассоциируемая с фотоном (или с другими частицами вроде электронов), описывает вероятность обнаружения частицы в некоторой области пространства. В задаче с интерферометром (см. рис. 3.4 и 5.1) одиночный фотон находился одновременно в первом и во втором плечах прибора при равной вероятности обнаружить его в обеих этих областях пространства. Чтобы лучше понимать и описывать положение фотона, необходимо подробнее обсудить свойства волн. Нужно понять природу волн амплитуды вероятности, в особенности то, как они объединяются и что происходит, когда выполняются измерения.

Проще всего начать с задачи о свободной частице, которую мы обсуждали в главе 2. Свободная частица может быть фотоном, электроном или бейсбольным мячом. Свободной она является в том случае, если на неё не действуют никакие силы — нет ни гравитации, ни электрического или магнитного поля, ни фотонов, сталкивающихся с электроном, ни бейсбольных бит, ударяющих по мячу, ни сопротивления воздуха — ничего подобного. В отсутствие сил, действующих на частицу, она имеет строго определённый неизменный импульс. Таким образом, если она движется в определённом направлении, она будет просто продолжать двигаться в этом направлении. Можно выбрать для этого направления любое обозначение: пусть, например, это будет направление x. Представим себе график с горизонтальной осью x. Мы просто выберем направление этой оси x вдоль направления движения частицы. Обсуждая рис. 2.5, мы говорили о классической частице, движущейся вдоль оси x с классическим импульсом p. Здесь мы поговорим о квантовой частице с импульсом p.

Частицы имеют длину волны

Импульс фотона определяется уравнением p=h/λ, где h — постоянная Планка, λ — длина волны света. Таким образом, импульс связан с длиной волны (цветом) света. Луи Виктор Пьер Раймон, герцог Брольи^{10}, получил Нобелевскую премию по физике в 1929 году

«за открытие волновой природы электрона».

Луи де Бройль теоретически показал, что такие частицы, как электроны или бейсбольные мячи, также имеют волновые свойства. Как рассказывается далее, волновое описание электронов, как и любых других типов частиц, даётся с помощью того же рода волн амплитуды вероятности, что были введены в главе 5 для описания фотонов.

Длина связанной с частицей волны равна λ=h/p. Это результат простого преобразования приведённой выше формулы для импульса фотона. Если обе части формулы для импульса фотона умножить на λ и разделить на p, то получится выражение для длины связанной с частицей волны. Важный результат, полученный де Бройлем, состоит в том, что связь между импульсом и длиной волны одинакова для фотонов (света) и для материальных частиц, таких как электроны и бейсбольные мячи. Поэтому свойства фотонов на фундаментальном уровне описываются точно так же, как свойства электронов и бейсбольных мячей. Длина волны, связанной с частицей, называется дебройлевской длиной волны. (В следующей главе мы покажем на физических примерах, почему кажется, будто бейсбольные мячи не обладают волновыми свойствами, тогда как у фотонов и электронов эти свойства заметны.)

Как выглядит волновая функция свободной частицы

Что представляет собой волновая функция свободной частицы с некоторым заданным значением импульса p? Вспомним, что волновая функция связана с вероятностью обнаружить частицу в некоторой области пространства. На рис. 6.1 представлен график волновой функции для свободной частицы с импульсом p. Как говорилось выше, длина волны связанной с этой частицей волновой функции равна λ=h/p. Из рисунка видно, что волновая функция свободной частицы представляется двумя волнами, которые называются действительной и мнимой компонентами волновой функции.

Рис. 6.1.Волновая функция свободной частицы с импульсом p, которая имеет длину волны λ=h/p. Квантовомеханическая волновая функция имеет две части, которые называются действительной и мнимой. Эти волны имеют одинаковую длину. Они лишь смещены одна относительно другой на четверть длины волны, что эквивалентно сдвигу на 90° по фазе. Эти две компоненты отделены друг от друга. Они не интерферируют ни конструктивно, ни деструктивно. Для свободной частицы с чётко определённым значением импульса p волновая функция простирается от плюс бесконечности до минус бесконечности (от +∞ до −∞)

Эти компоненты равноценны. Слово «мнимая» — это просто математический термин. Его не следует понимать так, будто мнимая компонента в каком-либо смысле менее важна, чем компонента, называемая действительной. Это просто такой жаргон для обозначения двух компонент, различающихся по своему математическому представлению. Действительная и мнимая компоненты волновой функции имеют одинаковую длину волны, но смещены на одну четверть длины волны. Это означает, что одна волна сдвинута по фазе относительно другой на 90°. Эти две компоненты волновой функции не интерферируют друг с другом ни конструктивно, ни деструктивно, поскольку и в математическом смысле, и по сути они перпендикулярны друг другу.

Частица с хорошо определённым импульсом размазана по всему пространству

Важная особенность волновой функции, показанной на рис. 6.1, состоит в том, что она тянется от плюс бесконечности до минус бесконечности (от +∞ до −∞). На рис. 6.1 видна лишь малая часть волновой функции в небольшой области пространства, поскольку на конечном листе бумаги нельзя изобразить график от +∞ до −∞. Волновая функция, представленная на этом рисунке, просто продолжается без изменений вправо и влево. Это означает, что квантовомеханическую частицу с чётко определённым значением импульса p мы с равной вероятностью найдём в любом месте вдоль оси x — горизонтальной оси на этом графике. По вертикальной оси отложена амплитуда вероятности обнаружить частицу в том или ином месте. Обе компоненты — действительная (пунктирная кривая) и мнимая (сплошная кривая) колеблются между положительными и отрицательными значениями. У обеих есть места, где они обращаются в нуль.

Тот факт, что волновая функция колеблется между положительными и отрицательными значениями, не важен. Для квантовомеханического объяснения интерференции фотона на рис. 5.1 была введена борновская интерпретация волновой функции. Согласно этой интерпретации, вероятность обнаружить частицу в некоторой области пространства равна квадрату абсолютной величины волновой функции в этой области пространства. Возведённая в квадрат волновая функция может приобретать только положительные значения, точно так же как 2²=4 и (−2)²=4, поскольку минус на минус даёт плюс. Обратите внимание, что на рис. 6.1, когда одна из двух волн обращается в нуль, другая волна находится на положительном или отрицательном максимуме. Когда одна волна мала, другая — велика. Когда волновая функция анализируется математически, то, как это видно из графика, абсолютная величина квадрата волновой функции оказывается одинаковой во всех точках оси x.

Абсолютная величина квадрата волновой функции для свободной частицы одинакова вдоль всей оси x — от +∞ до −∞. Таким образом, вероятность обнаружить частицу в любом месте пространства одинакова. Частица с одинаковой вероятностью найдётся в точке x=10, в точке x=−1000000 или где угодно ещё. Представьте себя крошечным созданием, которое часто называют демоном Максвелла. Вы стоите рядом с частицей-волной, изображённой на рис. 6.1. Вы пытаетесь схватить частицу. С некоторой вероятностью она окажется у вас в руках. Если вы станете делать это снова и снова, то в зависимости от размеров вашей руки вы сможете в конце концов поймать частицу. При этом каждый раз вам придётся начинать её ловлю заново. Если вы переместитесь вдоль волны в другое место и повторите попытку, вероятность поймать частицу не изменится. Именно в этом состоит смысл одинаковой вероятности обнаружить частицу где угодно. Для демона Максвелла нет предпочтительного места ловли частицы. Все места равноценны.

Этот образ свободной частицы, которая описывается волновой функцией, задающей равную вероятность обнаружить частицу в любом месте, не очень-то согласуется с нашим классическим представлением о частицах. На рис. 2.5 показана классическая частица, обладающая в заданный момент времени определённым значением импульса и положением. Обсуждая фотоэлектрический эффект (см. рис. 4.3), Эйнштейн описывал свет как фотоны, которые являются квантами света. Один фотон «выбивает» один электрон, и этот электрон вылетает из куска металла. Это описание выглядит так, как будто и фотон и электрон являются частицами в понимании классической механики. Однако при обсуждении интерференции фотонов (см. рис. 5.1) потребовалось использовать интерпретацию Борна и описывать фотоны как волны амплитуды вероятности, когда половина вероятности приходится на каждое плечо интерферометра. На рис. 6.1 график волновой функции свободной частицы полностью делокализован, то есть растянут на всё пространство. Это описание одинаково как для фотона, так и для электрона.

Интерференция волн разной длины

Так что же представляют собой фотоны, электроны, камни и всё остальное? Это частицы или волны? Чтобы убедиться в отсутствии противоречий в квантовомеханическом описании природы вещей, нам надо подробнее обсудить волны и их интерференцию. Обсуждая рис. 3.2 и 3.3, мы уже говорили о том, что волны могут интерферировать конструктивно, давая более крупную волну, и деструктивно — так, что получается волна меньшего размера или волны полностью гасят друг друга. В примерах, представленных на рис. 3.2 и 3.3, волны имеют одинаковую длину. Когда они складываются конструктивно (см. рис. 3.2), все положительные пики одной волны приходятся на положительные пики другой, и то же самое относится к отрицательным пикам, так что в результате их амплитуда увеличивается. Когда волны складываются деструктивно (см. рис. 3.3), положительные пики приходятся на отрицательные и наоборот, что приводит к их гашению. Однако волны разной длины тоже могут интерферировать.

На рис. 6.2 изображены графики пяти волн разной длины. Единицы измерения длины здесь не имеют значения. Важно то, что эти пять волн имеют длины λ, равные 1,2; 1,1; 1,0; 0,9 и 0,8. Фазы этих волн подогнаны так, чтобы они совпадали в точке x=0, где x — горизонтальная ось. Волны совпадают в точке x=0 в том смысле, что все они имеют в этом месте положительный пик. Однако поскольку волны имеют разную длину, их пики не обязательно будут совпадать в других точках вдоль оси x. Например, вблизи точек x=10 и −10 тёмно-серая волна имеет максимум, а светло-серая пунктирная — минимум. Вдобавок около точки x=10 одна волна имеет отрицательное значение, а другая — положительное. В окрестностях x=16 и −16 две волны имеют максимум, а одна волна — минимум. Важный момент здесь состоит в том, что при разной длине все волны могут совпадать в одной точке (x=0, например), но в общем случае, в других точках, одни волны будут положительными, а другие — отрицательными.

Рис. 6.2.Пять изображённых здесь волн имеют разную длину λ: 1,2; 1,1; 1,0; 0,9 и 0,8. Их фазы подобраны таким образом, чтобы пики всех волн приходились на точку 0 по горизонтальной оси. Однако поскольку волны имеют разную длину, они не совпадают в других местах в отличие от рис. 3.2. Обратите внимание на то, что вблизи точек x=10 и −10 тёмно-серая волна имеет положительный пик, тогда как пунктирная светло-серая волна — отрицательный

На рис. 6.3 показан результат суперпозиции (сложения) пяти волн с рис. 6.2. В точке x=0 (на горизонтальной оси) рис. 6.2 все волны точно совпадают по фазе. В результате их суперпозиция (сложение всех волн), представленная на рис. 6.3, здесь образует максимум. На рис. 6.2 эти волны совпадают по фазе только в точке строго x=0. Тем не менее вблизи x=0 различие в длинах волн ещё не даёт большого сдвига пиков одной волны относительно другой, так что волны остаются очень близкими по фазе. Другой набор максимумов возникает вблизи точек x=6 и −6. Однако эти максимумы не столь велики, как в точке x=0, поскольку, как видно на рис. 6.2, не все пики волн совпадают друг с другом. За пределами x=±10 амплитуда суперпозиции становится небольшой. В любой точке одни волны положительные, а другие — отрицательные, и это приводит к деструктивной интерференции. Поскольку имеется только пять волн, деструктивность этой интерференции оказывается лишь частичной.

Рис. 6.3.Суперпозиция пяти волн, изображённых на рис. 6.2. В точке x=0 (по горизонтальной оси) волны на рис. 6.2 находятся в фазе, так что они складываются конструктивно. Вблизи x=0 волны всё ещё очень близки по фазе, но следующие максимумы возле точек x=6 и −6 уже не столь велики, как максимум на x=0. В областях от 10 до 20 и от −10 до −20 вследствие разницы в длинах волн одни волны оказываются положительными, а другие — отрицательными. Здесь имеет место их значительное взаимное подавление

Рис. 6.4.Суперпозиция 250 волн с длинами, равномерно распределёнными в диапазоне от 0 до 4. По сравнению с рис. 6.3, где показана суперпозиция пяти волн, эта суперпозиция имеет значительно более выраженный пик при x=0, в области максимальной конструктивной интерференции, а деструктивная интерференция вызывает более сильное подавление в других областях. Амплитуда суперпозиции сходит на нет с приближением к отметке 20

На рис. 6.4 показана суперпозиция 250 волн разной длины. Длины этих волн равномерно распределены в диапазоне от 0 до 4. Как и в случае с пятью волнами (см. рис. 6.2) и их суперпозицией (см. рис. 6.3), все эти волны имеют одинаковую амплитуду. Фазы 250 волн подогнаны так, чтобы совпадать при x=0. Поскольку здесь волн гораздо больше и диапазон их длин шире, чем в случае, представленном на рис. 6.3, пик вблизи x=0 значительно уже и с удалением от него затухание происходит гораздо быстрее. Небольшие осцилляции возникают вследствие того факта, что все волны в суперпозиции имеют одинаковую амплитуду. Если амплитуда волны в середине распределения по длинам волн является наибольшей, а амплитуды других волн становятся всё меньше и меньше по мере удаления от средней длины волны, то можно получить суперпозицию, которая плавно спадает до нуля без набора убывающих по амплитуде осцилляций. Этот тип суперпозиции будет обсуждаться ниже.

Принцип суперпозиции

В главе 5 интерференционный эксперимент анализировался в терминах суперпозиции двух трансляционных состояний фотона: T₁ и T₂. Фотон в интерферометре описывается как находящийся в состоянии суперпозиции 50 на 50: T=T₁+T₂. Идея суперпозиции играет центральную роль в описании природы с точки зрения квантовой теории, а так называемый принцип суперпозиции утверждает, что «всякая система в определённом состоянии всегда может рассматриваться как находящаяся отчасти в каждом из двух или более состояний».

Исходное состояние может рассматриваться как суперпозиция двух или более состояний, подобно задаче с интерферометром, где трансляционное состояние фотона T может быть описано как суперпозиция T₁ и T₂. И наоборот, два или более состояния могут накладываться друг на друга, порождая новое состояние. Именно это, второе, утверждение мы будем использовать для понимания фундаментальной природы частиц. Тот факт, что фотон может вести себя как частица в случае фотоэлектрического эффекта и как волна при интерференции, вытекает из принципа суперпозиции и влечёт за собой принцип неопределённости Гейзенберга.

Собственные состояния

При обсуждении рис. 6.1 говорилось, что свободная частица с чётко определённым импульсом p представляет собой делокализованную волну амплитуды вероятности, распределённую по всему пространству. Про такую частицу говорят, что она находится в собственном состоянии по импульсу. При обсуждении задачи об интерференции мы называли T₁ и T₂ чистыми состояниями, однако их корректное название — собственные состояния. Собственное состояние для конкретной наблюдаемой физической величины, такой как импульс, — это состояние с чётко определённым значением данной величины.

Свободная частица, находящаяся в собственном состоянии по импульсу, полностью делокализована в пространстве. Для каждого из бесконечного числа возможных значений импульса существует по одномутакому собственному состоянию. Положение частицы однородно размазано по всему пространству, поскольку волновая функция, связанная с этим собственным состоянием, распределена по всему пространству. Однако, согласно принципу суперпозиции, новое состояние может быть образовано из любого числа собственных состояний по импульсу.

Суперпозиция волн амплитуды вероятности импульсных собственных состояний

Для понимания природы реальных частиц — фотонов, электронов и т. п. — мы будем строить суперпозиции волн амплитуды вероятности для целых диапазонов импульсных собственных значений, подобно тому как это было показано на рис. 6.1. Для каждого импульса p волна имеет свою длину: — λ=h/p. Из рис. 6.3 и 6.4 видно, что сложение волн с различными длинами приводит к концентрации амплитуды волны в определённой области пространства. Как отмечалось в обоих рассмотренных выше примерах, амплитуда всех волн в этих суперпозициях была одинаковой.

Теперь мы будем складывать импульсные волны амплитуды вероятности с различными амплитудами. Есть одна волна (определённое значение p) с наибольшей амплитудой. И чем больше другие волны отличаются от неё по длине, тем меньше их амплитуда. Длина волны с максимальной амплитудой находится в центре распределения. Под распределением имеется в виду просто диапазон длин волн. Представьте себе такую аналогию: комната, полная людей, которые распределены по возрасту. Некоторые люди будут иметь средний возраст, соответствующий центру распределения, другие будут старше или моложе среднего. В нашем случае имеется волна в центре распределения и другие волны — более короткие и более длинные.

Рис. 6.5. График вероятности обнаружить частицу в конкретном импульсном собственном состоянии, соответствующем импульсу p, задаётся как суперпозиция импульсных волн амплитуды вероятности. Значение p ₀ — это средняя волна с наибольшей амплитудой в данном распределении. Величина ∆p служит мерой ширины распределения собственных значений

На рис. 6.5 показано распределение волн амплитуды вероятности для импульсных состояний. Значение p₀ — это импульс волны в центре распределения. Она имеет длину λ=h/p₀. Это волна с наибольшей амплитудой, с наибольшей вероятностью обнаружения в данном распределении. При увеличении или уменьшении импульса относительно p₀ (λ соответственно будет меньше или больше) величина отдельной волны в суперпозиции (её вероятность) убывает. Величина ∆p служит мерой ширины распределения. Если значение ∆p велико, имеется большой разброс по p, а значит, и большая ширина распределения длин волн. Если значение ∆p мало́, то мала и ширина распределения длин волн.

Импульс свободной частицы в состоянии суперпозиции

Чему равен импульс свободной частицы, которая находится в суперпозиции собственных состояний импульса, как показано на рис. 6.5? Суперпозиция собственных состояний импульса означает, что мы просто складываем (накладываем друг на друга) группу волн (амплитуды вероятности), где каждой волне соответствует конкретное (собственное) значение импульса. При любом измерении любой характеристики — системы будет получено конкретное значение этой характеристики. Если мы измерим импульс частицы, то получим одно конкретное значение импульса. Природа возмущения, сопутствующего измерению абсолютно малого объекта, состоит в том, что состояние суперпозиции коллапсирует в одно-единственное собственное значение. Выполнение измерений меняет систему, переводя её из исходного состояния суперпозиции в одно из конкретных собственных значений. Именно это мы называем коллапсом.

При обсуждении задачи об интерференции говорилось, что если попытаться обнаружить, находится ли фотон в состоянии T₁, поместив детектор в первое плечо интерферометра, то состояние суперпозиции, необходимое для интерференции, будет разрушено. Состояние суперпозиции T превратится либо в T₁, либо в T₂. Поскольку состояние T является суперпозицией в равных пропорциях T₁ и T₂, в половине измерений результатом будет обнаружение системы в состоянии T₁, а в другой половине — T₂. В каждом конкретном измерении невозможно заранее узнать, какой будет получен результат. Большое число измерений покажет, что суперпозиция имеет пропорцию 50:50, поскольку в половине случаев фотон обнаружится в первом плече прибора (состояние T₁), а в половине случаев — во втором плече (состояние T₂).

Суперпозиция собственных значений импульса, показанная на рис. 6.5, состоит из огромного (бесконечного) числа состояний, лежащих в диапазоне импульсов, характеризуемом шириной распределения ∆p. Таким образом, существует широкий диапазон значений импульса, которые могут быть получены в любом отдельном измерении. Если выполнить единичное измерение, будет получено одно из множества этих значений.

Допустим, мы выполнили измерение и обнаружили, что импульс немного больше p₀. Обозначим его p₁, поскольку это наше первое измерение. В процессе выполнения измерения мы произвели возмущение системы, которым нельзя пренебречь. Она перешла из состояния суперпозиции в состояние с единственным собственным значением импульса p₁. Таким образом, для выполнения ещё одного измерения понадобится начать всё сначала и подготовить частицу (систему) тем же способом, которым она была подготовлена изначально, чтобы получить такое же распределение импульсов.

Теперь выполняем второе измерение. На этот раз мы получаем значение, которое несколько меньше p₀. Обозначим его p₂. Вновь подготовим систему и выполним ещё одно измерение. Назовём результат p₃. Каждый раз, выполняя измерения одинаково подготовленных систем, мы будем получать разные конкретные значения импульса. Заранее неизвестно, какое получится значение. Если выполнить очень много измерений, можно построить график вероятности получения различных значений p. Такой график даст распределение, подобное тому, что представлено на рис. 6.5. Невозможно предсказать, какое значение будет получено в отдельном измерении. Однако кое-что нам всё же известно. Весьма маловероятно, что будет получено значение p, которое намного больше или намного меньше p₀, поскольку распределение имеет очень малую амплитуду на краях диапазона. Скорее всего, измеренное значение p будет находиться вблизи p₀, потому что именно в этой части распределения велика амплитуда.

Импульс частицы в состоянии суперпозиции определён не вполне чётко

Частица, находящаяся в суперпозиции собственных состояний импульса, вроде представленной на рис. 6.5, не имеет чётко определённого значения импульса. Нельзя предсказать, какое его значение будет получено в одном конкретном измерении. Можно утверждать, что, скорее всего, будет получено значение, близкое к p₀. Выполнив много измерений, можно найти распределение вероятности.

Классическая частица, подобная той, что показана на рис. 2.5, имеет чётко определённое значение импульса. Измерить это значение можно, не изменяя его. Если частица свободна, можно выполнять новые измерения импульса в разные моменты времени, и всегда будет получено одно и то же значение p. Однако это совсем не так в случае абсолютно малых квантовых частиц, находящихся в состоянии суперпозиции по импульсу. В единичном измерении мы получим одно конкретное значение p, но сам акт измерения фундаментальным образом меняет природу частицы. Частица переходит из состояния суперпозиции в одно из собственных состояний (одиночная волна с единственным значением импульса). Из состояния, в котором существует распределение вероятности по импульсам, частица переходит в состояние с единственным значением импульса — тем, которое наблюдалось. Чтобы восстановить распределение, частицу необходимо подготовить заново.

Где находится частица, когда она пребывает в состоянии суперпозиции по импульсу?

При обсуждении рис. 6.1 говорилось, что частица, находящаяся в отдельном собственном состоянии импульса, делокализована по всему пространству. Это совсем не согласуется с описанием фотоэлектрического эффекта, поэтому теперь возникает вопрос: где находится частица, которая пребывает в состоянии суперпозиции? Определённый намёк на ответ мы уже получили, обсуждая рис. 6.2–6.4. Из рис. 6.3 и 6.4 видно, что суперпозиция волн разной длины порождает распределение, которое концентрируется в некоторой области пространства. На рис. 6.3 длина волны изменяется от 0,8 до 1,2 и распределение выглядит не столь сильно сконцентрированным в одной области, как на рис. 6.4, где длина волны изменяется от 0 до 4. На рис. 6.6 показано пространственное распределение, соответствующее распределению волн (импульсных собственных состояний), изображённому на рис. 6.5. Есть положение, где пространственное распределение достигает максимума, и это положение также является средним. Для значений x, больших и меньших, чем x₀, амплитуды (вероятности) становятся меньше.

Рис. 6.6.График вероятности обнаружения частицы в точке x, когда она находится в суперпозиции собственных состояний по импульсу, показанной на рис. 6.5. Точка x₀ соответствует среднему положению с наибольшей вероятностью. Величина ∆x служит мерой ширины пространственного распределения

Что означает распределение вероятности положений (значений x)? Частица с распределением вероятности по импульсам, изображённым на рис. 6.5, даёт пространственное распределение вероятности, представленное на рис. 6.6. Одиночное измерение положения даёт конкретное значение координаты. Обозначим его x₁. Выполнение измерения абсолютно малой квантовой частицы вызывает возмущение, которым нельзя пренебречь, что приводит к коллапсу пространственного распределения вероятности до собственного значения с чётко определённой координатой. Чтобы выполнить другое измерение, систему (частицу) надо подготовить заново прежним способом, тогда она будет иметь такое же распределение вероятности по импульсу и, следовательно, такое же пространственное распределение вероятностей. Второе измерение положения частицы даст значение x₂, которое в общем случае не будет совпадать с x₁. Если, подготавливая систему вновь и вновь, выполнить много измерений положения, обнаружится распределение вероятности по координате, изображённое на рис. 6.6. Величина ∆x служит мерой ширины пространственного распределения. Пространственное распределение, изображённое на рис. 6.6, определённое по множеству измерений идентично подготовленных систем, говорит о вероятности получить при измерении любое конкретное значение положения. С наибольшей вероятностью измерение обнаружит частицу где-то вблизи точки x₀, но для любого отдельного измерения невозможно сказать, где будет найдена частица. В то же время мала вероятность получить при измерении положения значение, далёкое от x₀.

Волновые пакеты

Частица, находящаяся в суперпозиции собственных состояний импульса, как это показано на рис. 6.5, называется волновым пакетом. Импульс её более или менее известен — с точностью до величины ∆p. Поскольку импульс — это произведение массы и скорости, а массу частицы мы знаем, то нам примерно известна её скорость. Чем больше ∆p (чем шире распределение импульсов в волновом пакете), тем хуже определён импульс, а значит, при отдельных измерениях будут получаться значения импульса, лежащие в более широком диапазоне. Волновой пакет также растянут и по положению. Частица не находится в конкретной точке x, как в классической физике. Существует разброс координат, задаваемый распределением вроде того, что изображён на рис. 6.6, а количественно его можно охарактеризовать шириной распределения ∆x.

Разброс по импульсу и координате

На рис. 6.7 изображены два волновых пакета. В верхней части показан волновой пакет, состоящий из сравнительно широкого распределения собственных состояний импульса. Большой разброс собственных состояний импульса (большое значение ∆p) приводит к относительно узкому пространственному распределению (малому значению ∆x). В нижней части рисунка показан волновой пакет, составленный из сравнительно узкого распределения собственных значений импульса (с малой величиной ∆p), что приводит к большому разбросу в пространственном распределении (большой величине ∆x).

Связь между ∆p и ∆x, проиллюстрированная на рис. 6.7, носит универсальный характер. Волновой пакет, охватывающий большой диапазон импульсов (с большой неопределённостью импульса), будет иметь небольшой разброс по положению (малую неопределённость координаты). Эта взаимосвязь порождается интерференцией. Волновой пакет, составленный из широкого набора собственных значений импульса, обладает широким спектром длин волн, поскольку каждому собственному значению импульса соответствует волна амплитуды вероятности длиной λ=h/p.

Рис. 6.7.Распределение вероятности импульса (p) и распределение вероятности координаты (x) для двух волновых пакетов. В верхней части имеет место широкий разброс p (большое значение ∆p), который порождает малый разброс по x (малое значение ∆x). В нижней части разброс по p мал (∆p мало́), что приводит к увеличению разброса по x (∆x велико)

Все волны амплитуды вероятности в пакете могут конструктивно интерферировать в некоторой точке пространства. Однако, как показано на рис. 6.2, с удалением от этой центральной точки конструктивной интерференции нарастает деструктивная интерференция. В любой точке, далёкой от этого центра, одни волны будут положительными, а другие — отрицательными (см. рис. 6.2). Когда разброс длин волн велик, большая разница в длинах волн приводит к тому, что деструктивная интерференция начинается очень близко от центральной точки максимальной конструктивной интерференции, и пакет оказывается узким (большое значение ∆p, малое — ∆x). Когда разброс по длинам волн мал, то есть длины волн различаются несущественно, надо значительно удалиться от центральной точки идеальной конструктивной интерференции, чтобы добраться до места, где равное число волн имеет положительные и отрицательные значения. В этом случае значение ∆p мало́, а ∆x — велико.

Ввиду особой важности представления о разбросе по импульсу и о связанном с ним разбросе по координате давайте ещё раз рассмотрим смысл разброса. Всё это связано с экспериментами. В отдельном эксперименте по измерению импульса частицы может быть получено лишь одно значение. У вас есть некоторый инструмент. Он выдаёт одно число. Он не может сообщить, что импульс равен одновременно 10 и 50. Каким же образом мы получаем одно значение, если наш пакет обладает распределением импульсов?

Волновой пакет состоит из суперпозиции собственных значений импульса, то есть импульсных волн амплитуды вероятности, однозначно связанных со значениями импульса. Когда выполняется измерение, сопутствующее ему непренебрежимое возмущение заставляет систему «перепрыгнуть» из состояния суперпозиции в определённое собственное состояние. Измерение даёт значение импульса, которое соответствует данному собственному состоянию. Обратите внимание на то, что измерение меняет систему. Чтобы выполнить ещё одно измерение, нужно начать сначала и подготовить частицу тем же способом, что и в первый раз. При повторении процедуры подготовления волнового пакета он будет состоять из той же суперпозиции собственных значений импульса. Теперь выполним то же самое измерение, что и в первый раз. В общем случае мы получим другое значение импульса, поскольку волновой пакет состоит из множества импульсных волн, с каждой из которых связано своё наблюдаемое значение импульса.

Выполнив огромное число измерений, мы можем получить значение 400 (единицы в данном случае не важны) тысячу раз, значение 390 — восемьсот раз, 410 — восемьсот раз, но 200 и 600 — только по двадцать раз. Если по всем этим числам построить график, получится распределение вероятности, подобное тем, что показаны для импульса в левой части рис. 6.7. Такое распределение вероятности — это результат экспериментального определения состава волнового пакета. Теперь мы знаем, какова величина (вероятность) каждой волны в пакете. Такое же описание применимо и к положению нашего волнового пакета. Каждое измерение положения волновых пакетов, подготовленных идентичным образом, даёт одно положение зарегистрированной частицы. После множества измерений получается распределение по координате, подобное тем, что представлены в правой части рис. 6.7.

Принцип неопределённости Гейзенберга

Чрезвычайно важной является связь между разбросом по импульсу и разбросом по координате, играющая фундаментальную роль в описании частиц в состоянии суперпозиции. Когда разброс по импульсу (∆p) велик, вдоль оси x распределено множество волн (см. рис. 6.1), которые вместе образуют волновой пакет. Эти волны имеют различную длину (см. рис. 6.2). Когда интерферирует множество волн в широком диапазоне длин, область конструктивной интерференции очень быстро заканчивается с удалением от места, где она максимальна (см. рис. 6.3 и 6.4). Это означает, что разброс по координате (∆x) мал. Если же волновой пакет состоит лишь из небольшого спектра импульсных волн (значение ∆p мало́), область конструктивной интерференции тянется в пространстве гораздо дальше от точки максимума пространственного распределения (см. рис. 6.7). Соответственно величина разброса, или неопределённости положения (∆x), оказывается большой. Всё это происходит в силу того, что волновые функции, которые описывают собственные значения импульсов, являются по своей природе волнами амплитуды вероятности. Местоположением волнового пакета можно в каком-то смысле считать область конструктивной интерференции, а в областях существенной деструктивной интерференции вероятность обнаружить частицу очень мала.

Формальное соотношение между разбросом по импульсу и разбросом по координате, то есть между ∆p и ∆x, называется принципом неопределённости Гейзенберга. Вернер Карл Гейзенберг (1901–1976) получил Нобелевскую премию по физике в 1932 году

«за создание квантовой механики, приложения которой, в числе прочего, привели к открытию аллотропных форм водорода».

Принцип неопределённости Гейзенберга выражается простым математическим соотношением: ∆x∙∆p≥h/4π, где h — постоянная Планка, а ∆x и ∆p задают ширину распределений координаты и импульса, как показано на рис. 6.7. (Символ ≥ означает «больше или равно».) Какой будет знак — «равно» (=) или «больше» (>), — зависит от формы распределений вероятности. Знак «равно» соответствует гауссовой кривой, названной так в честь великого математика Карла Фридриха Гаусса (1777–1855). Кривые, изображённые на рис. 6.5–6.7, представляют собой гауссовы кривые. Это стандартные «колоколообразные кривые», которые описывают такие распределения, как, например, число баллов, полученных на экзамене, при правильно подготовленном тесте и достаточном числе людей, которые его сдают. Кривые Гаусса часто встречаются в физике. Знак «больше» применим при других формах распределения. Для любой формы кривой, построенной по конкретному распределению волн, можно определить, каким будет произведение ∆x∙∆p, но оно всегда >h/4π, если только кривая не является гауссовой.

Для понимания природы принципа неопределённости важно рассмотреть случай гауссовых кривых, подобных тем, что изображены на рис. 6.7. В этом случае ∆x∙∆p=h/4π. Данное уравнение показывает, какая информация может быть одновременно известна о положении и импульсе частицы. Величина h/4π является константой. Таким образом, произведение ∆x∙∆p равно константе. Следовательно, если неопределённость импульса ∆p велика, то неопределённость положения ∆x должна быть мала, чтобы их произведение составляло h/4π. С другой стороны, если значение ∆p мало́, то значение ∆x — велико.

Связь между ∆p и ∆x проиллюстрирована на рис. 6.7. Принцип неопределённости гласит, что вы можете знать кое-что об импульсе частицы и кое-что о её положении, но вы не можете точно знать и положение, и импульс частицы в одно и то же время. Эта неопределённость — невозможность одновременно знать и положение, и импульс частицы — резко контрастирует с классической механикой. Для классической теории совершенно принципиально то, что, как показано на рис. 2.5, положение и импульс частицы могут быть точно известны (измерены) одновременно. Квантовая теория утверждает, что невозможно одновременно точно знать положение и импульс. Они могут быть известны лишь с некоторыми неопределённостями — ∆x и ∆p.

Анализируя соотношение для принципа неопределённости ∆x∙∆p=h/4π, рассмотрим, что случится, если делать ∆p всё меньше и меньше. Разделив обе части уравнения на ∆p, получаем:

∆x=h/4π∙∆p.

Поскольку ∆p уменьшается, делитель становится всё меньше и меньше, а значит, ∆x возрастает. В пределе, когда ∆p устремляется к нулю, ∆x стремится к бесконечности. Этот предел имеет глубокий смысл. Если ∆p обращается в нуль, импульс известен совершенно точно, но положение становится совершенно неопределённым. При ∆x=∞ частицу можно с равной вероятностью обнаружить где угодно.

Этот результат согласуется с тем, что мы выяснили, обсуждая рис. 6.1, на котором показан вид волновой функции для собственных значений импульса. Когда частица находится в собственном состоянии импульса, значение её импульса определено совершенно точно. Однако её функция амплитуды вероятности, которая описывает вероятность обнаружить частицу в некоторой области пространства, размазана (делокализована) по всему пространству. Во всех точках вероятность обнаружить частицу одинакова: ∆x=∞. Это контрастирует с волновыми пакетами, изображёнными на рис. 6.7, где суперпозиция собственных состояний импульса порождает состояние, в котором больше нет идеально точно определённого импульса, но зато имеется некоторая информация о положении. Положение и импульс известны с точностью до их неопределённости.

Можно преобразовать соотношение для неопределённостей следующим образом:

∆p=h/4π∙∆x.

Отсюда видно, что в пределе, когда ∆x стремится к нулю (идеально точно определённое положение), ∆p стремится к бесконечности. Если нам совершенно точно известно положение, импульс может иметь любое значение. Волновой пакет, составленный из всех собственных значений импульса (∆p=∞), имеет совершенно точно определённое положение. Можно точно узнать p, но лишь ничего не зная об x; можно точно узнать x, но лишь ничего не зная о p. Это называется дополнительностью. Можно узнать x или p, но не то и другое одновременно.

В классической механике можно знать x И p. В квантовой механике можно знать x ИЛИ p. В общем случае для квантовых — абсолютно малых — частиц можно узнать кое-что о p и кое-что об x, но невозможно узнать точно то и другое одновременно.

7. Фотоны, электроны и бейсбольные мячи

И фотоны, и электроны, и бейсбольные мячи в равной мере описываются квантовой теорией, но для описания последних эта теория не является необходимой. Мячи ведут себя как обычные частицы и в этом отношении с высокой точностью описываются классической механикой. Если и для фотонов, и для электронов, и для мячей подходит одинаковое квантовомеханическое описание, почему только мячи ведут себя как классические частицы? Ответ заключается в том, что мячи являются большими в абсолютном смысле. В этой главе мы разберёмся, почему фотонам и электронам требуется квантовое описание, а бейсбольным мячам — нет. Здесь обсуждаются реальные физические ситуации, в которых проявляется как волновая, так и корпускулярная природа квантовых, то есть имеющих малые в абсолютном смысле размеры, частиц.

Волны или частицы?

Когда частица находится в состоянии суперпозиции, то есть представляет собой волновой пакет, мы обладаем некоторой информацией о её положении и некоторой информацией о её импульсе. Так чем же являются фотоны, электроны и подобные им объекты — волнами или частицами? Ответ состоит в том, что они являются волновыми пакетами. Покажутся они вам частицами или волнами, зависит от выполняемого эксперимента, то есть от вопроса, который вы задаёте.

Если предметом эксперимента является фотоэлектрический эффект, фотоны ведут себя как частицы. Один фотон толкает один электрон и выбивает его из металла (см. рис. 4.3). Фотон — это волновой пакет, порождённый набором импульсных собственных состояний. Набор с широким разбросом ∆p даёт относительно хорошо определённое положение, то есть относительно небольшое значение ∆x. В этом случае фотонный волновой пакет имеет более или менее определённое положение и может вести себя как частица света в электрическом эффекте.

В интерференционном эксперименте (см. рис. 5.1) фотоны ведут себя как волны. Это не должно удивлять, поскольку волновой пакет фактически и является суперпозицией волн, но не волн в обычном классическом смысле, а волн амплитуды вероятности. Обсуждая явления интерференции, мы рассматривали фотонную волну как единую волну амплитуды вероятности. Теперь ясно, что в действительности это волновой пакет, представляющий собой суперпозицию волн. Попадая на расщепляющее пучок полупрозрачное зеркало, он становится суперпозицией двух трансляционных состояний: T₁ и T₂. Волны амплитуды вероятности состояния T₁ интерферируют с соответствующими волнами состояния T₂ и порождают интерференционную картину, которая обсуждалась выше.

Дифракция света

Итак, фотон ведёт себя как частица в случае фотоэлектрического эффекта, но может также вести себя и как волна. Эксперимент, ясно демонстрирующий волновые свойства фотонов, — это дифракция света на дифракционной решётке. Дифракцию можно наблюдать с помощью музыкального компакт-диска (CD) на ярком свету, например солнечном. На поверхность CD нанесены очень тонкие канавки. Это дорожки, на которых хранится информация. Как объясняется далее, при падении на CD белого света от солнца или лампочки канавки вызывают его дифракцию, отчего каждый цвет отражается в своём направлении. Разные участки CD расположены под разными углами относительно вашего глаза, из-за чего они зрительно окрашиваются в разные цвета.

Дифракция на решётке используется в оптических инструментах, называемых спектрометрами. Эти инструменты разделяют входящий в них свет на цвета, так что цвета можно анализировать по отдельности. Запись цветов, составляющих свет от конкретного источника, называется спектром. Например, звёзды испускают свет различного цвета в зависимости от их температуры. Получение спектра звёздного света даёт массу информации о звезде. На своём пути через космос звёздный свет встречает различные молекулы. В главе 8 и далее рассказывается о том, что разные молекулы поглощают свет разных цветов. Поэтому по пути к Земле некоторые цвета звёздного света частично поглощаются космическими молекулами. Астрономы устанавливают спектрометры на телескопах и снимают спектры, чтобы определить, какие молекулы находятся между Землёй и конкретной звездой.

На рис. 7.1 показана геометрия дифракции света на решётке. Входящий свет падает на решётку под углом α (греческая буква «альфа») к нормали. Нормаль — это направление, перпендикулярное поверхности. На рисунке мы смотрим на решётку сбоку. Поверхность решётки, которая глазу кажется плоским зеркалом, плотно покрыта идущими параллельно друг другу канавками. Эти канавки называют штрихами. На рис. 7.1 расстояние между штрихами обозначено буквой d. Это расстояние сравнимо с длиной волны света и составляет около одной десятимиллионной метра. Канавки обладают высокой отражательной способностью. Обычно они покрыты золотом или серебром. Если входящий свет состоит из набора цветов, то отражённый свет разделяется по цветам так, что свет каждого цвета следует в своём уникальном направлении. Это разделение света по цветам проиллюстрировано на рис. 7.1. На рисунке угол между нормалью к решётке и направлением конкретного — голубого — цвета обозначен β (греческая буква «бета»). Для зелёного цвета угол β будет больше, а для красного — ещё больше.

Рис. 7.1.Геометрия дифракции света на решётке. Решётка представляет собой отражающую поверхность, обычно серебряную или золотую, покрытую очень тонкими параллельными канавками. Показан вид решётки сбоку. Сама она уходит за страницу. Все канавки находятся на строго постоянном расстоянии d друг от друга; α — угол входящего света. Свет отражается под углом β, зависящим от его цвета. В результате дифракции происходит разделение цветов

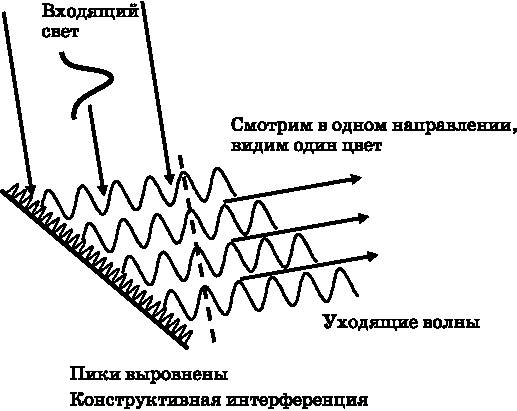Рис. 7.2. Входящие фотонные волновые пакеты испытывают дифракцию на решётке. От канавок отражается свет различных цветов. Для каждого цвета существует направление, в котором волны соответствующего цвета интерферируют конструктивно. Они складываются, давая большую амплитуду волны, так что цвет выглядит очень ярким именно в этом направлении

Дифракция света демонстрирует волновую природу фотонов

Дифракция света на решётке демонстрирует волновую природу фотонных волновых пакетов. Для того чтобы понять, каким образом дифракция выявляет волновой характер фотонов, нужно рассмотреть механизм дифракции с точки зрения конструктивной и деструктивной интерференции волн. На рис. 7.2 входящий фотонный волновой пакет показан как луч света, падающий на дифракционную решётку. Чтобы достичь разных частей решётки, свету приходится пройти разное расстояние. Свет, попадающий на верхнюю левую часть решётки, проходит меньший путь, чем свет, падающий на нижнюю правую её часть. Волновой пакет состоит из множества цветов, то есть множества волн разной длины λ.

Свет разных цветов будет расходиться от решётки по всем направлениям. Однако здесь-то и начинаются тонкости. Волновые пакеты более или менее локализованы, но они состоят из различных цветов, каждый из которых представляет собой делокализованную волну амплитуды вероятности (см. рис. 6.1, 6.2, 6.4 и 6.7). Более или менее локализованный волновой пакет образуется за счёт интерференции множества волн разного цвета (с разными λ, которым соответствуют разные импульсы p). Рассмотрим один конкретный цвет — красный, который составляет часть волнового пакета. Если волна падает только на один штрих решётки, то из-за формы канавки она отразится по множеству направлений. От этой канавки она уйдёт в состояние суперпозиции волн амплитуды вероятности, распространяющихся по множеству направлений. В интерферометре (см. рис. 5.1) входящий волновой пакет переходит в состояние суперпозиции, волны амплитуды вероятности которого распространяются по двум направлениям. Здесь же после попадания на одиночный штрих суперпозиция будет распространяться по множеству направлений.

Важная особенность решётки состоит в том, что входящая волна падает на множество её штрихов. Для конкретного цвета, например красного, как показано на рис. 7.2, имеется одно направление, в котором волны будут складываться конструктивно. На данном рисунке для направления, в котором распространяются красные волны, пики и впадины этих волн складываются в фазе, несмотря на то что отражаются они в разных местах. (Длина волны на рисунке была преувеличена по сравнению с расстоянием d между штрихами, чтобы было лучше видно выравнивание волн.) Синфазное сложение множества волн, уходящих от решётки, делает отражённую волну очень большой. На всех остальных направлениях красные волны будут складываться деструктивно, поскольку пики и нули не выровнены друг с другом.

Дифракция на решётке заставляет волны определённой длины (конкретного цвета) конструктивно складываться в одном направлении. Интенсивность света, связанная с амплитудой вероятности световой волны, пропорциональна квадрату амплитуды волны. Поэтому в направлении конструктивной интерференции для конкретного цвета, например красного, интенсивность света оказывается велика. В других направлениях красный свет будет испытывать деструктивную интерференцию, поскольку его длина волны такова, что разность расстояний до каждой канавки не равна целому числу длин волн. Для другого цвета, скажем голубого, существует другое направление, вдоль которого свет, приходящий от всех канавок, будет складываться конструктивно (см. рис. 7.1). Поэтому голубая составляющая входящего фотонного волнового пакета будет покидать решётку в виде волны большой амплитуды в своём собственном направлении, и в этом направлении интенсивность голубой составляющей входящего света будет выглядеть очень большой.

Электроны в кинескопе ведут себя как снаряды

Дифракция света на решётке выявляет волновые свойства фотонных волновых пакетов, в то время как фотоэлектрический эффект демонстрирует их корпускулярные свойства, соответствующие большей степени локализации. При обсуждении длины волны де Бройля, которая связана с импульсом соотношением p=h/λ, говорилось, что описание электронов и других типов «частиц» аналогично описанию фотонов. И фотоны, и электроны описываются посредством волн амплитуды вероятности. И те и другие представляют собой более или менее локализованные волновые пакеты (см. рис. 6.7). Для электрона, представляющего собой свободную частицу (в отсутствие действующих на него сил), волновой пакет является суперпозицией импульсных собственных состояний свободной частицы. Неопределённость положения электрона ∆x зависит от неопределённости (разброса) по импульсу ∆p согласно соотношению неопределённостей Гейзенберга: ∆x∙∆p≥h/4π. Равенство здесь соблюдается для гауссовых волновых пакетов, которые имеют форму, показанную на рис. 6.7.

Чтобы проиллюстрировать как волновую, так и корпускулярную природу электронов, рассмотрим два примера: работу кинескопа (электронно-лучевой трубки, ЭЛТ) и дифракцию низкоэнергетических электронов на поверхности кристалла. Кинескопы применяются весьма широко. Это устройства, которые создают изображение в старых телевизорах и компьютерных дисплеях. Правда, в последнее время громоздкие телевизоры и мониторы, основанные на ЭЛТ, практически полностью вытеснены другими устройствами, такими как жидкокристаллические (ЖК) дисплеи. (Существует несколько технологий, используемых для больших плоских телевизоров, но все плоские компьютерные мониторы — жидкокристаллические.)

На рис. 7.3 схематично изображено устройство ЭЛТ. Внутри ЭЛТ создаётся вакуум, в котором электроны могут двигаться, не сталкиваясь с молекулами воздуха. Процесс создания картинки начинается с нити накаливания — отрезка проволоки, изображённой в левой части рисунка. Электрический ток, который проходит по этой нити, сильно разогревает её подобно спирали обычной лампы накаливания, нагревательному элементу электрокамина или электрического обогревателя. Тепло, выделяемое этой нитью, нагревает катод, и он тоже становится очень горячим. Катод — это кусок металла, на который подано отрицательное напряжение, как на отрицательном конце батарейки, но значительно большее по величине. Катод становится настолько горячим, что с него начинают испаряться электроны. Тепло — это форма энергии. Электроны удерживаются в металле энергией связи, которая зависит от типа металла. Когда металл достаточно сильно разогревается, тепловая энергия может превосходить энергию связи электрона, и некоторые электроны будут покидать металл. При фотоэлектрическом эффекте энергию, необходимую для выхода электрона из металла, приносит фотон. В ЭЛТ эту энергию обеспечивает тепло. Электроны, покидающие металл, замещаются благодаря подключению катода к отрицательному полюсу источника питания, который поставляет на их место другие электроны, делая процесс непрерывным. Электроны — это отрицательно заряженные частицы, и поскольку на катод подано отрицательное напряжение, катодом испускаются электроны. Итак, электроны вылетают из катода. Уходу электронов от катода помогает положительно заряженная сетка (см. рис. 7.3). Поскольку эта сетка соединена с положительным полюсом источника питания, отрицательно заряженные электроны притягиваются к ней. Одинаковые заряды отталкиваются друг от друга, противоположные заряды притягиваются. Сетка состоит из тонких проводков с большими просветами между ними. Когда электроны достигают сетки, большинство из них пролетает сквозь неё, продолжая движение с очень большой скоростью.

Рис. 7.3. Схема электронно-лучевой трубки (ЭЛТ). Нить накаливания разогревает катод, из которого «испаряются» электроны. Положительно заряженная сетка ускоряет отрицательно заряженные электроны. Напряжение, приложенное к управляющим сеткам, направляет электроны в конкретную точку экрана. Экран покрыт крошечными тесно прилегающими друг к другу пятнами красного, зелёного и голубого люминофора, которые при попадании электронов светятся соответствующим цветом. Изображение на экране создаётся за счёт того, что электронный луч, быстро перемещаясь, попадает по нужным цветовым пятнам

Затем электроны проходят между управляющими сетками (см. рис. 7.3), которые влияют на направление их движения. Одна пара управляющих сеток (изображена на рисунке) меняет направление в вертикальной плоскости, а другая пара (не показана) — в горизонтальной плоскости. Рассмотрим вертикальную плоскость. Если на верхнюю управляющую сетку подано положительное напряжение, а на нижнюю — отрицательное, электроны будут отклоняться вверх, как показано на рис. 7.3, поскольку отрицательно заряженные электроны притягиваются к положительно заряженной верхней сетке и отталкиваются от отрицательно заряженной нижней.

Если поменять полярность напряжения на этих двух сетках, электроны станут отклоняться вниз. Если к сеткам приложено большое напряжение, электроны будут отклоняться сильно. При слабом напряжении электроны отклоняются незначительно. Если не подавать никакого напряжения, электроны будут двигаться прямо. То же самое происходит, когда напряжение прикладывается к горизонтальным управляющим сеткам. Пройдя мимо управляющих сеток, электроны движутся далее по прямой. В этом отношении электронами можно стрелять как снарядами. Эта часть ЭЛТ называется электронной пушкой. Электронные пушки используются во многих научных приборах, таких как электронные микроскопы и устройство, которое мы рассмотрим далее. Так что и после того, как ЭЛТ окончательно исчезнут из телевизоров и компьютерных дисплеев, устройство, которое мы только что обсудили, останется очень важным.

Учитывая отсутствие воздуха и то, что сила гравитации очень мала, электроны движутся практически как свободные частицы, пока не столкнутся с экраном, изображённым в правой части рис. 7.3. На экране находятся очень маленькие и очень тесно расположенные пятна люминофоров. Люминофоры — это химические соединения, которые испускают свет, будучи возбуждёнными, то есть когда им сообщается достаточная энергия. В данном случае люминофоры возбуждаются, когда в них врезаются электроны. В каждой маленькой области экрана находятся три пятна люминофоров — красного, зелёного и голубого. Электронный луч можно с высокой точностью нацелить на любое из этих пятен. Если в данном месте находится красный люминофор, на экране мгновенно зажигается крохотная красная точка. Если электронный луч попадает на зелёный люминофор, появляется точка зелёного цвета, а если на голубой люминофор — голубая.

Электроника, подающая напряжение на управляющие сетки, заставляет электронный луч пробежать по экрану горизонтально, затем немного отпускает его и снова заставляет пересечь экран горизонтально. Так продолжается до тех пор, пока луч не пробежит по всему экрану. Тогда луч возвращается наверх, и весь процесс повторяется. Пробегая по экрану, луч попадает на пятна красного, зелёного и голубого люминофора. Пятнышки этих трёх люминофоров расположены настолько близко друг другу по горизонтали и вертикали, что глаз не различает их как отдельные точки. Также луч можно выключить, и тогда, если ни один из люминофоров не возбуждён, получается чёрное пятно. Сочетания трёх названных цветов достаточно для получения любого цвета. Управляя тем, по каким цветовым пятнам стрелять электронами, а по каким нет, можно получить изображение, которое мы видим на экране телевизора или на компьютерном ЭЛТ-дисплее.Электронный луч движется по экрану очень быстро, и глаз не может различить, что в действительности мы смотрим на последовательность сменяющихся с очень большой частотой статических картинок.

В этом описании работы ЭЛТ поведение электронов очень похоже на поведение частиц в нашем обычном представлении. Ими можно стрелять из электронной пушки и попадать в очень маленькие пятнышки на экране. Это не слишком похоже на поведение волн. И всё же это укладывается в наше описание более или менее локализованных волновых пакетов. Пока ∆x электронного волнового пакета значительно меньше размера пятнышек люминофора (пикселов), тот факт, что эти волновые пакеты локализованы в масштабе расстояний ∆x, не имеет значения. Хотя цветные пикселы маленькие, они не являются «абсолютно малыми» по шкале размеров. Они достаточно малы, чтобы мы не могли увидеть их без микроскопа, но всё равно достаточно велики в сравнении с масштабами длины, которые встречаются в атомных и молекулярных системах. Поэтому волновые пакеты даже с достаточно малым ∆p всё равно имеют неопределённость положения, очень малую по сравнению с размерами пиксела.

Для любой частицы, и в частности для электрона, p=m∙V, где m — масса, а V — его скорость. Масса электрона чётко определена. Неопределённость p возникает из-за неопределённости скорости, то есть смысл ∆p состоит в том, что скорость не является чётко определённой. Измерения скорости идентично подготовленных электронных волновых пакетов не будут раз от раза давать одинаковые результаты. Неопределённость скорости приводит к неопределённости импульса (∆p), что, согласно принципу неопределённости (∆x∙∆p≥h/4π), приводит к неопределённости x (∆x). Важный момент заключается в том, что величина ∆x может быть значительной в масштабах атомов и молекул, но очень мала по сравнению с масштабами длины макроскопических цветных пикселов на ЭЛТ-экране. В таких ситуациях волновая природа волновых пакетов не проявляется и они ведут себя, как классические частицы.

При дифракции электроны ведут себя как волны

Как показано на рис. 7.4, электронные волновые пакеты тоже демонстрируют волновые свойства. В изображённом эксперименте пучок электронов, сгенерированный электронной пушкой, подобной описанной выше, направляется не на телевизионный экран, а на поверхность кристалла. Электроны недостаточно энергичны, чтобы проникнуть в кристалл. На поверхности кристалла атомы выстроены в ряды, называемые кристаллической решёткой. Эти ряды атомов разделены интервалами в несколько ангстремов. (Один ангстрем — это единица длины, равная 10⁻¹⁰ м, или одной десятимиллиардной метра. Ангстремы часто используются в атомных масштабах, для их обозначения служит символ Å.) Указанный интервал определяется размерами атомов. Ряды атомов работают как штрихи дифракционной решётки, но они расположены гораздо плотнее. Длина волны электронов относится к тому же масштабу расстояний, что и шаг решётки (интервал между рядами). Длина волны определяется формулой де Бройля: λ=h/p, где p=m∙V. Масса электрона составляет 9,1∙10⁻³¹ кг. При скорости 7,3∙10⁵ м/сек (730 км/сек) длина волны составит: λ=10 Å. Такая скорость легко достигается в простейшей электронной пушке.

Электронные волны амплитуды вероятности испытывают дифракцию на поверхности кристалла подобно фотонам на обсуждавшейся выше дифракционной решётке. Однако дифракционная решётка обладает единственным шагом d, поскольку все канавки идут параллельно друг другу в одном направлении. Решётка же на поверхности кристалла двумерная. Как видно на рис. 7.5, у неё имеется много направлений, вдоль которых располагаются параллельные ряды атомов. В качестве примеров на рисунке сплошными линиями обозначены некоторые ряды атомов, идущие в разных направлениях. Штриховыми линиями, параллельными сплошным, показано, что для каждого из таких направлений существует параллельный ряд атомов. Ряды атомов, идущие в разных направлениях, разделены разными расстояниями (интервалами между дифракционными канавками). Различие этих интервалов наглядно показано на рис. 7.5: обратите внимание на расстояния между парами параллельных сплошной и штриховой линий. Каждая пара разделена своим расстоянием, соответствующим интервалу между канавками.

Рис. 7.4. Схема дифракции низкоэнергетических электронов на поверхности кристалла. Входящий пучок электронов низкой энергии не проникает в кристалл, отражаясь от поверхности. Ряды атомов действуют подобно канавкам дифракционной решётки на рис. 7.1. Они вызывают дифракцию приходящих электронных волн

Рис. 7.5. Решётка с рис. 7.4, на которой показаны примеры рядов атомов, идущих в различных направлениях. Для каждой прямой, проходящей через центры атомов, образующих ряд, можно провести другие параллельные ей прямые, которые также проходят через центры атомов. Интервалы между этими параллельными рядами различаются. Каждый набор рядов вызывает дифракцию в своём направлении

Поскольку существует множество межатомных интервалов для «канавок», идущих в разных направлениях, электронные волны будут испытывать дифракцию по многим различным направлениям. На рис. 7.6 приведён пример дифракции низкоэнергетических электронов на поверхности кристалла. Чёрный круг в центре — это кусок металла, называемый поглотителем пучка. Его поддерживает другая металлическая деталь, которая на изображении выглядит как тёмная вертикальная полоска под ним. Поглотитель не позволяет части электронного пучка, которая отразилась от кристалла, попасть в детектор. Яркие и тусклые белые пятна порождаются испытавшими дифракцию электронами, которые попали в детектор. По положению пятен можно определить расположение атомов и интервалы между ними. Анализ дифракции электронов на кристаллах — это важный метод научного исследования их поверхности. Рисунок электронной дифракции убедительно демонстрирует, что электроны, как и фотоны, ведут себя подобно волнам.

Рис. 7.6. Экспериментальные данные, демонстрирующие дифракцию электронов на поверхности кристалла. Светлые пятна соответствуют различным направлениям, в которых распространяются испытавшие дифракцию электроны. Этих пятен много, поскольку дифракция происходит на многих различных параллельных рядах атомов (см. рис. 7.5)

Электроны и фотоны — это частицы и волны, а бейсбольные мячи — это лишь частицы

Электроны в ЭЛТ ведут себя как частицы, подобно фотонам в фотоэлектрическом эффекте. Низкоэнергетические электроны ведут себя как волны при дифракции на поверхности кристалла, что аналогично поведению фотонов, когда они испытывают дифракцию на дифракционной решётке. На самом деле фотоны, электроны и все остальные частицы являются волновыми пакетами, которые в большей или меньшей степени локализованы. Волновые пакеты могут демонстрировать свои волновые или корпускулярные свойства в зависимости от обстоятельств.

Если фотоны и электроны могут демонстрировать как волновые, так и корпускулярные свойства, то почему такого не бывает с бейсбольными мячами? Чтобы понять, почему мячи ведут себя как частицы с позиций классической механики, необходимо рассмотреть, как соотносятся размеры частиц и длины связанных с ними волн.

Рассмотрим для начала электрон в атоме водорода. Мы будем обсуждать квантовое описание атома водорода и других атомов в главах 10 и 11, а сейчас используем лишь простые количественные оценки волновых параметров атома водорода. Согласно формуле де Бройля, длина волны определяется формулой λ=h/p. Импульс равен p=m∙V, то есть произведению массы и скорости. Масса электрона составляет m_e=9,1∙10⁻³¹ кг, а характерная скорость электрона в атоме — V=5,0∙10⁶ м/сек. Тогда длина волны де Бройля составляет

λ=h/p = (6,6∙10⁻³⁴ Дж∙сек)/[(9,1∙10⁻³¹ кг)∙(5,0∙10⁶ м/сек)] = 1,5∙10⁻¹⁰ м = 1,5 Å.

Заметим, что значение 1,5 Å примерно соответствует размеру атома. Таким образом, длина волны электрона в атоме и размеры атома примерно одинаковы. Волновые свойства электронов становятся очень важны, когда электроны оказываются в очень маленьких системах, таких как атомы.

А что можно сказать о бейсбольном мяче? По правилам Главной лиги бейсбола мяч должен весить от 142 до 149 г. Примем его массу равной 145 г = 0,145 кг. При очень сильной подаче развивается скорость 145 км/ч = 40 м/сек. Импульс быстрого мяча составляет p= 0,145 кг ∙ 40 м/сек = 5,8 кг∙м/сек. Таким образом, длина волны де Бройля для такого мяча будет равна

λ=h/p = (6,6∙10⁻³⁴ Дж∙сек)/[(0,145 кг)∙(40 м/сек)] = 1,1∙10⁻³⁴ м = 1,1∙10⁻²⁴ Å.

Это невероятно малая величина. Размер одного атома составляет около 1 Å, размер ядра атома — примерно 10⁻⁵ Å. Следовательно, длина волны бейсбольного мяча составляет 0,0000000000000000001 размера атомного ядра. Такая длина волны чрезвычайно мала — настолько, что она никогда не проявится ни при каких измерениях. Ни у какой дифракционной решётки не может быть столь малого шага, чтобы продемонстрировать дифракцию волн длиной в одну десятимиллионную от триллионной доли размера атомного ядра. Поскольку эта длина волны та́к мала́, нам не приходится беспокоиться о том, что мяч может испытать дифракцию на бейсбольной бите. Он всегда ведёт себя как классическая частица.

Объекты, которые велики в абсолютном смысле, обладают тем свойством, что ассоциированная с ними длина волны совершенно ничтожна по сравнению с их размерами. Поэтому крупные частицы демонстрируют только свою корпускулярную природу, а их волновая природа никогда не проявляется. Напротив, для частиц, которые малы в абсолютном смысле, длина волны де Бройля сопоставима с их размерами. Такие абсолютно малые частицы ведут себя как волны или как частицы в зависимости от ситуации. Они представляют собой волновые пакеты. В контексте нашего обсуждения они являются и волнами, и частицами.

8. Квантовый ракетбол и цвет фруктов

В предыдущих главах были введены и объяснены фундаментальные понятия квантовой теории. Приведённые примеры, однако, касались только поведения свободных частиц. Было показано, что электроны могут вести себя как частицы, когда обсуждается работа ЭЛТ, но они ведут себя как волны, когда речь идёт о дифракции на поверхности кристаллов.

Свободная частица может иметь любую энергию. Эта энергия, которая является кинетической, определяется массой и скоростью частицы. Небольшое приращение скорости даёт небольшой прирост энергии. Значительное увеличение скорости приведёт к существенному увеличению энергии. Шаги изменения энергии могут быть любой величины; она меняется непрерывным образом.

О связанных электронах мы говорили только вскользь, в связи с фотоэлектрическим эффектом. При этом подчёркивалось, что если энергии приходящего фотона недостаточно для преодоления связи электронов с металлом, то ни одного электрона из него не вылетит. Электроны, связанные с атомными ядрами, отвечают за свойства атомов и молекул. Выше упоминалось о том, что Планк объяснил излучение абсолютно чёрного тела, которое будет подробно обсуждаться далее, постулировав, что энергия связанных электронов может меняться только дискретными шагами. Чтобы понять свойства атомной и молекулярной материи, окружающей нас в повседневной жизни, необходимо уметь в квантовой теории работать со связанными электронами.

Ключевое свойство электронов, связанных с атомами и молекулами, состоит в том, что их энергетические состояния дискретны. Мы говорим, что энергия электрона может квантоваться, то есть электрон, связанный с атомом или молекулой, может иметь лишь некоторые определённые значения энергии. Энергия меняется ступенчато, и эти ступени имеют определённые дискретные размеры. Энергетические состояния подобны лестнице. Вы можете стоять на одной ступени или подняться на следующую, более высокую ступень. Однако невозможно стоять на полпути между двумя ступенями. Эти дискретные, или квантованные, значения энергии часто называют энергетическими уровнями. В отличие от обычных лестниц интервалы между энергетическими уровнями, как правило, не одинаковы.

Важная сфера современных квантовых исследований — расчёт электронных состояний молекул. Эта область называется квантовой химией. Такие вычисления позволяют получить квантованные уровни энергии для электронов в молекулах (энергетические уровни), а также рассчитать строение молекул. Расчёт строения молекулы даёт расстояния между атомами и положения всех атомов в молекуле с точностью, ограниченной лишь принципом неопределённости. Таким образом, квантовомеханические расчёты позволяют определять размеры и форму молекул. Подобные вычисления важны для понимания фундаментальных принципов связывания атомов в молекулы и для конструирования новых молекул. По мере развития квантовой теории и появления всё более мощных и сложных компьютеров, способных решать трудоёмкие математические задачи, всё более и более крупные молекулы удаётся исследовать методами квантовой химии. Одно из наиболее важных приложений квантовой теории — разработка фармацевтических препаратов. Молекулы можно конструировать так, чтобы они имели нужные размеры и «подходили» по форме к конкретным локусам протеинов или энзимов.

Квантовая химия требует очень трудоёмких вычислений. Даже для простейшего атома водорода квантовомеханические расчёты математически очень сложны. Атом водорода состоит из одного электрона, связанного с одним протоном. Протон, который является ядром атома водорода, — это положительно заряженная частица, а электрон заряжен отрицательно. Притяжение отрицательно заряженного электрона к положительно заряженному протону удерживает их вместе, скрепляя атом водорода. Детали расчёта энергетических уровней атома водорода здесь излагаться не будут, но в следующих главах мы рассмотрим некоторые особенности результатов этих вычислений. Они дают энергетические уровни атома водорода и его волновые функции. Именно волновые функции, то есть волны амплитуды вероятности для атома водорода, являются отправной точкой для понимания всех атомов и молекул. Атомы и молекулы сложны потому, что они являются абсолютно малыми трёхмерными системами, и необходимо учитывать, как протоны и электроны взаимодействуют друг с другом.

Частица в ящике — классический случай

Есть очень простая задача, имеющая отношение к нашей теме. Она известна как задача о частице в ящике. Для её решения не нужна сложная математика, однако это решение позволяет проиллюстрировать важные свойства связанных электронов, например квантование уровней энергии и волноподобную природу электронов в связанных состояниях. Прежде чем анализировать природу электрона в одномерном ящике атомных размеров, обсудим классическую задачу об идеальной одномерной игровой площадке для ракетбола, чтобы выявить различия между классической (большой) и квантовомеханической (абсолютно малой) системами.

На рис. 8.1 изображён идеальный «ящик». Он одномерный. Его стенки считаются бесконечно высокими, бесконечно массивными и совершенно непроницаемыми. Внутри ящика нет воздуха, который оказывал бы сопротивление движению. На рисунке внутренняя часть ящика обозначена Q=0, а внешняя — Q=∞. Ранее говорилось, что свободной называют такую частицу, на которую не действуют никакие силы. Силы возникают, когда частица с чем-то взаимодействует. Например, отрицательно заряженная частица, такая как электрон, может взаимодействовать с положительно заряженным протоном. Взаимодействие в виде притяжения между противоположно заряженными частицами будет порождать силу, действующую на электрон. При управлении электронами в ЭЛТ (см. рис. 7.3) электрическое поле порождает силу, действующую на электроны и заставляющую их менять направление.

Мера взаимодействия частицы с чем-то влияющим на неё, вроде электрического поля, называется потенциалом и имеет размерность энергии. В дальнейшем потенциал будет обозначаться буквой Q. Внутри ящика Q=0, как в случае свободной частицы. Это означает, что частица не взаимодействует ни с чем внутри ящика. Здесь нет ни электрических полей, ни сопротивления воздуха. Однако снаружи ящика Q=∞. Бесконечный потенциал означает, что частица должна была бы обладать бесконечной энергией, чтобы оказаться в областях вне ящика. Выражение Q=∞ — это просто способ формализации утверждения о том, что стенки ящика являются идеальными. Частица не может проникнуть сквозь стенки или перепрыгнуть через них, сколь бы велика ни была её энергия. Если поместить частицу в такой ящик, она не может ускользнуть и всегда будет оставаться внутри него. В этом смысле частица заперта в ящике. Она может находиться в области пространства длиной L, но нигде больше.

Рис. 8.1. Идеальный одномерный ящик. Его стенки бесконечно высокие, бесконечно толстые, бесконечно массивные и совершенно непроницаемые. В ящике нет сопротивления воздуха. Внутри ящика потенциальная энергия Q равна нулю, а снаружи — бесконечности. Ящик имеет длину L

На рис. 8.2 изображён мяч для игры в ракетбол, отскакивающий от стенок идеальной одномерной классической (большой) ракетбольной площадки. Как уже было сказано, эти стенки идеальные, а внутри нет сопротивления воздуха. Кроме того, мяч тоже идеален, то есть обладает абсолютной упругостью. Когда мяч сталкивается со стенкой, он сжимается, как пружина, и снова распрямляется, что вызывает его отскок. Реальные мячи не идеально упругие. Когда мяч сжимается при ударе, не вся энергия, затраченная на его сжатие, идёт на отталкивание от стены. Часть энергии, затраченной на сжатие мяча, идёт на его нагрев. Однако здесь мы будем считать мяч идеально упругим. При ударе о стену вся кинетическая энергия мяча, которая обусловливает его сжатие, расходуется затем на отталкивание мяча от стены. Поэтому скорость мяча перед самым столкновением со стеной равна скорости его отскока после столкновения.

Рис. 8.2. Мяч на идеальной одномерной ракетбольной площадке. Сопротивление воздуха отсутствует, а мяч идеально упруг. Когда мяч ударяется об стену в точке L, он отскакивает, ударяется об стену в точке 0 и продолжает отскакивать взад и вперёд, поскольку площадка идеальна, мяч идеален и нет сопротивления воздуха. Начав так отскакивать, мяч будет бесконечно долго продолжать двигаться туда-обратно

На этой идеальной ракетбольной площадке мяч отскакивает от стен без какой-либо потери энергии; кроме того, нет ни сопротивления воздуха, ни гравитации. Поэтому мяч будет вечно двигаться туда-обратно, отражаясь от стен. Он ударится о стену в точке L, отскочит, столкнётся со стеной в точке 0, снова отскочит и будет продолжать своё движение взад и вперёд. Внутри ящика, поскольку потенциал равен нулю (см. рис. 8.1), никакие силы на мяч не действуют. Поэтому его энергия является чисто кинетической:

E_k=½m∙V²,

где m — масса мяча, а V — его скорость. Если мяч испытает слабые внешние воздействия, его скорость станет немного меньше и значение E_k тоже немного уменьшится. В этом идеальном ракетболе энергия может меняться непрерывным образом. Значение E_k может увеличиваться или уменьшаться произвольным образом в зависимости лишь от силы воздействия на мяч.

Другая важная особенность классического ракетбола — это возможность остановить мяч так, чтобы он неподвижно лежал на полу. В этой ситуации его скорость равна нулю: V=0. А раз V=0, то и E_k=0. При V=0 импульс тоже равен нулю, поскольку p=m∙V, так что импульс известен нам точно. Если мяч лежит на полу (V=0), то его положение известно. Если обозначить это положение x (см. рис. 8.2), то значение x будет находиться в интервале от 0 до L. Величина x не может принимать никакие другие значения, поскольку мяч находится на площадке (в ящике) и не может оказаться снаружи из-за идеальных стенок. Мяч можно поместить в определённое положение x на полу площадки, и тогда его положение будет известно точно. Это свойство макроскопической игровой площадки, даже идеальной. Это классическая система, и в ней можно точно и одновременно знать импульс p и положение x.

Площадка для игры в ракетбол имеет длину 12 м, диаметр мяча составляет 5,6 см, а его вес — около 0,04 кг. Очевидно, что игра в ракетбол описывается классической механикой. С помощью света можно следить за отскоками мяча туда-обратно, не влияя на них.

Частица в ящике — квантовый случай

Что изменится, если теперь мы перейдём к рассмотрению квантового ракетбола? Площадка остаётся идеальной, но теперь её длина не 12 м, а 1 нм (10⁻⁹ м). Кроме того, частица обладает массой электрона, равной 9,1∙10⁻³¹ кг, а не 0,04 кг. Таким образом, это задача о квантовой частице в ящике.

Сразу можно сказать, что наименьшая энергия квантовой частицы в ящике нанометрового размера не может быть нулевой. На классической ракетбольной площадке возможна скорость мяча V, равная нулю, а значит, нулевым может быть и импульс p=m∙V. Кроме того, положение мяча x имеет чётко определённое значение. Например, мяч может лежать неподвижно (V=0) точно посередине площадки, что соответствует x=L/2. В таком случае для нашего классического ракетбольного мяча ∆p=0 и ∆x=0. Значение произведения ∆x∙∆p=0 не соответствует принципу неопределённости Гейзенберга, что нормально, поскольку речь идёт о классической системе. Однако абсолютно малая частица в ящике нанометрового размера является квантовым объектом и должна подчиняться принципу неопределённости, утверждающему, что ∆x∙∆p≥h/4π. Если V=0 и x=L/2, то мы знаем одновременно x и p, а значит, ∆x∙∆p=0, как в классическом ракетболе. Для квантовой системы это невозможно. Таким образом, V не может быть равно нулю. Частица не может неподвижно пребывать в заданной точке. А если значение V ненулевое, то и значение E_k не может быть равно нулю. Принцип неопределённости говорит, что наименьшая энергия нашего квантового ракетбольного мяча не может быть нулевой. Квантовый мяч никогда не пребывает в неподвижности.

Значения энергии квантовой частицы в ящике

Какой энергией может обладать квантовая частица в ящике нанометровых размеров? На этот вопрос можно ответить без сложных расчётов, но сначала нам нужно вновь вернуться к волнам. В главе 6 мы говорили о волновых функциях свободных частиц. Волновая функция свободной частицы с определённым импульсом p — это волна, которая простирается по всему пространству. Таким образом, электрон с идеально определённым импульсом — это делокализованная волна, охватывающая всё пространство. Вероятность обнаружить свободный электрон всюду одинакова. Такой электрон обладает чётко определённой кинетической энергией E_k=½m∙V², поскольку имеет чётко определённый импульс p=m∙V.

Электрон в нанометровой коробке подобен нашей свободной частице в том, что касается внутренней области коробки, где Q=0. Внутри коробки отсутствует потенциал, а значит, нет и действующих на частицу сил. В этом отношении она очень похожа на свободную частицу, на которую тоже не действуют никакие силы. Однако есть важное различие между частицей в коробке и свободной частицей — это стенки ящика. Электрон в ящике находится только внутри ящика. Идеальный характер ящика не позволяет его волновой функции распространиться на всё пространство. Частица находится внутри ящика и никогда не может оказаться снаружи. Волновая функция задаёт амплитуду вероятности обнаружить частицу в некоторой области пространства. Это борновская интерпретация волновой функции. Если наш электрон может быть обнаружен только внутри ящика и никогда снаружи, то вероятность его обнаружения в ящике должна быть конечной, а вовне — нулевой. Если вероятность найти частицу вне ящика равна нулю, то и волновая функция должна быть равна нулю во всех точках вне ящика.

Итак, мы пришли к выводу, что волновая функция частицы в ящике подобна волновой функции свободной частицы, но волновая функция должна быть равна нулю вне ящика. В своей интерпретации природы квантовомеханической волновой функции Борн наложил некоторые физические ограничения на форму, которую может принимать волновая функция. Одно из них состоит в том, что хорошая волновая функция должна быть непрерывной. Это условие означает, что волновая функция должна плавно меняться от места к месту. Бесконечно малое изменение положения не может приводить к неожиданному скачку вероятности. Это очень простая мысль. Если вероятность обнаружить частицу в некоторой очень малой области пространства составляет, например, 1 %, то смещение на невообразимо малую величину не может вдруг сделать вероятность обнаружения частицы равной 50 %. Это ясно по изображениям волновых пакетов на рис. 6.7. Вероятность плавно меняется от места к месту. Это позволяет нам кое-что добавить к описанию волновых функций частицы в ящике помимо того факта, что они являются волнами с конечными амплитудами внутри ящика и нулевой амплитудой вовне. Поскольку волновая функция должна быть непрерывной, непосредственно у стенки ящика с внутренней стороны она должна иметь нулевую амплитуду, чтобы совпадать с нулевой амплитудой волновой функции вне ящика.

На рис. 8.3 показан (запрещённый) разрыв волновой функции внутри ящика. Волновая функция обозначена φ (греческая буква «фи»). По вертикальной оси отложена амплитуда волновой функции. Штриховой линией показан её нулевой уровень. Волновые функции, представляющие собой волны амплитуды вероятности, могут колебаться между положительными и отрицательными значениями. Волновая функция, представленная на рис. 8.3, имеет возле стенок значения, отличные от 0. Однако волновая функция должна быть нулевой вне ящика, то есть для значений x меньше 0 и больше L она должна быть равна нулю. На рисунке волновая функция неожиданно перескакивает от ненулевого значения у стенки внутри ящика к нулевому значению сразу за стенкой вне ящика. Таким образом, волновая функция, изображённая на рис. 8.3, не является допустимой, поскольку она не является непрерывной. Эта функция не может представлять квантовую частицу в ящике.

Рис. 8.3.Разрывная волновая функция внутри ящика. Волновая функция обозначена φ. По вертикальной оси отложена амплитуда волновой функции. Штриховой линией показано, где волновая функция обращается в нуль; это значение она должна иметь вне ящика. Волновая функция имеет ненулевое значение у стенок внутри ящика и затем должна скачкообразно (негладко) стать равной нулю вне ящика

Волновая функция должна иметь нулевое значение у стенок

Чтобы волновые функции, представляющие частицу в ящике, были физически приемлемыми, их значения у стенок должны быть нулевыми, и тогда они не будут испытывать разрыва на стенках. Выполнить это условие нетрудно. На рис. 3.1 показана волновая функция в свободном пространстве. Она колеблется между положительными и отрицательными значениями. Каждый раз, переходя от положительных значений к отрицательным или от отрицательных к положительным, она проходит через ноль. На самом деле нулевые точки отделены друг от друга половиной длины волны. Поэтому для получения хороших волновых функций частицы в ящике мы должны выбирать волны, длина которых позволяет им укладываться в ящике так, чтобы нулевые точки находились как раз на стенках.

Рис. 8.4.Три примера волновых функций φ внутри ящика, которые являются непрерывными. Для ясности они сдвинуты друг относительно друга по вертикали. По вертикальной оси отложена амплитуда волновой функции. Штриховая линия показывает, где волновая функция равна нулю, что должно соблюдаться вне ящика. Волновые функции, имеющие нулевые значения на стенках, непрерывны на них

На рис. 8.4 приведены три примера волн, которые подходят на роль волновых функций для частицы в ящике. Нижняя из них обозначена n=1 и состоит из одной полуволны. Она начинается слева на амплитуде 0, проходит максимум и затем снова опускается до нуля на стенке в точке L. Следующая волна, расположенная выше и обозначенная n=2, состоит из одного полного колебания. Она тоже начинается у левой стенки на амплитуде 0, проходит положительный пик, возвращается к нулю, затем следует отрицательный пик и возвращение к нулю на стенке в точке L. Волна, обозначенная n=3, содержит полтора периода. Подходит любая волна, содержащая целое число полуволн, то есть 1, 2, 3, 4, 5 и так далее половин длины волны, и расположенная так, чтобы она начиналась на нуле слева и заканчивалась на нуле справа.

Величина n — это число полуволн конкретной волновой функции. При n=1 длина волны λ составляет 2L, поскольку длина ящика равна L, а n=1 соответствует половине длины волны. При n=2 длина волны составляет L, поскольку ровно одна длина волны помещается между стенками. При n=3 между стенками помещаются три полуволны, то есть 1,5λ=L. В этом случае λ=L/1,5, то есть λ=⅔L. Обратите внимание, что здесь обнаруживается общее правило: λ=2L/n, где n — целое число. Для n=1 получаем λ=2L, для n=2 — λ=2L/2, для n=3 — λ=⅔L и т. д.

Узлы — это точки, где волновая функция проходит через ноль

Узлы — это ещё одна важная особенность волновых функций. Узлы — это точки, где волновая функция пересекает нулевую линию, переходя от положительных значений к отрицательным или от отрицательных к положительным. Волновая функция n=1 не имеет узлов. У волновой функции n=2 один узел располагается ровно посередине ящика. Волновая функция n=3 имеет два узла. Узлы — это точки, где (помимо стенок) вероятность обнаружить частицу равна нулю. В классической системе, такой как на рис. 8.2, мяч движется взад-вперёд. Он может находиться в любом месте. Однако для частицы в квантовом ящике есть определённые места (узлы), где вероятность обнаружить её равна нулю. Сколько бы измерений идентично подготовленных систем ни выполнялось, мы никогда не обнаружим частицу в узле.

На рис. 8.4 изображены волны амплитуды вероятности. Как уже говорилось, вероятность обнаружить частицу в некоторой области пространства пропорциональна квадрату волновой функции (в действительности квадрату её абсолютной величины, но для наших целей это не важно). На рис. 8.5 представлены квадраты волновых функций, изображённых на рис. 8.4. Квадраты волновых функций всегда положительны, поскольку вероятность обнаружить частицу в некоторой области пространства не может быть отрицательной. Там, где амплитуда велика, частица может быть обнаружена с большей вероятностью. С увеличением n число узлов возрастает. В следующей главе и далее будет показано, что атомные и молекулярные волновые функции имеют узлы.

Рис. 8.5. Квадраты первых трёх волновых функций φ ² для частицы в ящике. Для ясности они сдвинуты друг относительно друга по вертикали. По вертикальной оси отложен квадрат волновой функции амплитуды. Штриховая линия показывает, где волновая функция равна нулю. Квадраты волновых функций всегда положительны — они соответствуют вероятности. Волновые функции, изображённые на рис. 8.4, могут быть положительными или отрицательными

Часто спрашивают: как же частицы проходят через узлы? Например, при n=2 имеется узел, расположенный ровно посередине ящика. В классической системе, если мяч находится в левой части ящика и движется направо, но нам говорят, что он никогда не появится в центре ящика, то мы уверены, что мяч не достигнет правой стороны ящика. Однако такие рассуждения в классическом стиле неприменимы к абсолютно малым частицам, таким как электрон в ящике молекулярного размера. Он не обладает одновременно определёнными положением и импульсом, которые соответствовали бы наблюдаемой траектории. Квантовые частицы (в данном случае электрон) описываются как волны амплитуды вероятности. Волны имеют узлы. Они есть даже у классических волн. Квантовая частица «проходит через» узел, поскольку она является делокализованной волной амплитуды вероятности. Представление о траектории, двигаясь вдоль которой от точки A до точки B частица должна пройти все промежуточные точки между ними, просто неприменима к корректному волновому описанию электронов и других абсолютно малых частиц.

Значения энергии квантуются

Теперь мы определим возможные значения энергии, которой может обладать абсолютно малая частица в ящике. Классический мяч на ракетбольной площадке может иметь любую энергию, то есть набор её возможных значений непрерывен. Определить, какой энергией может обладать такая частица, как электрон в крошечном ящике, можно, опираясь на правило для возможных значений длины волны λ=2L/n амплитуды вероятности в этом ящике (см. рис. 8.4). Слово «крошечный» означает здесь, что ящик мал в абсолютном смысле, то есть длина волны сопоставима с его размерами. Нам также понадобятся несколько других физических соотношений, которые уже встречались нам ранее, а именно: соотношение для длины волны де Бройля p=h/λ, где p — импульс, а h — постоянная Планка; формула для импульса p=m∙V, где m — масса частицы, а V — её скорость; выражение для кинетической энергии частицы

E=½m∙V².

Давайте объединим эти формулы.

Первым делом возведём в квадрат величину p:

p²=m²∙V².

Если теперь разделить обе части уравнения на 2∙m, то в правой части получим кинетическую энергию

½m∙V²,

а в левой части —

p²/2∙m.

Отсюда следует выражение для кинетической энергии:

E=p²/2∙m.

Используя соотношение де Бройля, можно получить выражение: p²=h²/λ². Подставляя его в выражение для энергии, получаем:

E=h²/2∙m∙λ².

Наконец, применим наше правило λ=2L/n для возможных значений длины волны. Из него следует: λ²=4L²/n². Подставив это выражение в формулу для энергии, находим:

E=n²h²/8∙m∙λ²,

где n принимает любые целые значения: 1, 2, 3 и т. д. Целочисленная величина n называется квантовым числом.

Мы получили очень важный результат: значения энергии абсолютно малой частицы в абсолютно малом ящике. Этот результат очень тесно связан с поведением электронов в атомах и молекулах. Как видно из формулы, набор возможных значений энергии не непрерывен, поскольку n может принимать только целочисленные значения; другие величины, входящие в формулу, для конкретной системы являются константами. Мы будем говорить, что энергия квантуется, то есть она может принимать лишь некоторые значения, определяемые физическими свойствами системы и квантовым числом.

Дискретный набор энергетических уровней

Существует дискретный набор энергетических уровней для данных значений массы m и размера ящика L. Поскольку квантовое число n принимает значения 1, 2, 3 и т. д., соответствующие значения энергии будут равны

h²/8∙m∙L², 4∙h²/8∙m∙L², 9∙h²/8∙m∙L², и т. д.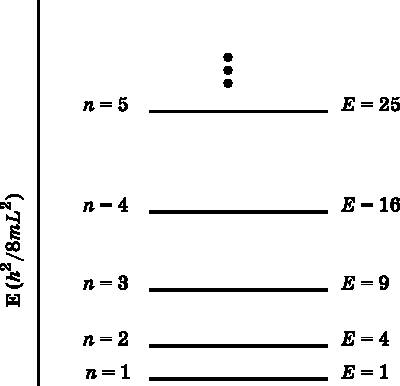

Рис. 8.6.Энергетические уровни частицы в ящике. Здесь n — квантовое число, а E — энергия, которая увеличивается как квадрат квантового числа. Энергия выражена в единицах h²/8∙m∙L², так что хорошо видно, как она возрастает. Штриховой линией обозначена нулевая энергия. Самый низкий энергетический уровень не совпадает с линией E=0 в отличие от случая классической частицы в ящике

На рис. 8.6 представлена диаграмма энергетических уровней для первых нескольких значений энергии частицы в ящике. Энергия выражена в единицах h²/8∙m∙L². Чтобы получить фактическое значение энергии, нужно просто подставить конкретные значения m и L в формулу для энергетических уровней. На диаграмме видно, что энергия увеличивается как квадрат квантового числа n. Штриховой линией обозначено, где энергия равна нулю. Квантовая частица в ящике на наинизшем энергетическом уровне имеет ненулевую энергию, чем резко отличается от классической частицы в ящике. На классической ракетбольной площадке энергия, которой может обладать мяч, непрерывна. Ударяя по мячу чуть сильнее или чуть слабее, его энергию можно увеличить или уменьшить на любую величину. Однако в квантовом ракетболе возможны лишь отдельные значения энергии, показанные на рис. 8.6. Как отмечалось в начале нашего разговора о квантовой частице в ящике, наименьшая энергия не равна нулю. Если бы квантовая частица в ящике могла иметь нулевую энергию, это нарушало бы принцип неопределённости.

Связь результатов для частицы в ящике с реальными системами

Частица в ящике — это очень простая иллюстрация общего свойства абсолютно малых систем. Энергия таких систем не обязательно непрерывна. Частица в ящике не является физически реализуемой системой, поскольку она одномерна и окружена «идеальными» стенками. Однако атомы и молекулы — реальные системы. Энергетические уровни атомов и молекул исследовались очень подробно, а их квантованные энергетические уровни измерялись экспериментально и рассчитывались теоретически. Подобно тому как энергетические уровни частицы в ящике зависят от свойств системы (массы частицы и длины ящика), энергетические уровни в атомах и молекулах зависят от свойств этих атомов и молекул.

Молекулы поглощают свет определённых цветов

Хотя частица в ящике не является физически реализуемой системой, свойства, обнаруженные в этой задаче, также присущи атомам и молекулам. При фотоэлектрическом эффекте энергия падающих фотонов столь велика, что из куска металла выбиваются электроны (см. главу 4). При достаточно большой энергии фотона его удар по молекуле также может привести к выбросу электрона. Однако в случае более низкой энергии фотонов при падении света на атом или молекулу он может поглощаться без испускания электронов. Внутренняя энергия атома или молекулы при этом возрастает, поскольку к ней добавляется энергия фотона.

Молекулы (и атомы) состоят из заряженных частиц: электронов, заряженных отрицательно, и атомных ядер, несущих положительный заряд. В видимом и ультрафиолетовом диапазонах, то есть при длине волны менее 700 нм, частота света очень велика. Колеблющееся электрическое поле света взаимодействует с заряженными частицами молекул. Электроны очень лёгкие, и поэтому им проще откликнуться на быстрые колебания электрического поля света видимого или ультрафиолетового диапазона. Поглощение видимого излучения и ультрафиолета вызвано увеличением энергии электронов в молекуле.

Вопрос состоит в том, какова длина световых волн, которые будут поглощаться молекулой? Это очень сложный вопрос для любой конкретной молекулы. Чтобы теоретически определить спектр поглощения молекулы, приходится выполнять огромное количество квантовомеханических расчётов. Тем не менее важные аспекты молекулярного поглощения света можно разобрать на основе задачи о частице в ящике. В качестве чрезвычайно упрощённой модели молекулы мы будем рассматривать одиночный электрон в ящике молекулярного размера. В конце мы подставим в формулы числа. Когда на электрон, находящийся в ящике (молекуле), никакой свет не падает, он пребывает в состоянии с наименьшей энергией, так называемом основном состоянии. Для частицы в ящике наименьшей энергии соответствует квантовое число n=1. При n=1

E=h²/8∙m∙L².

Когда на молекулу попадает свет, фотон может быть поглощён. В этом случае общая энергия света убывает на величину энергии поглощённого фотона. Энергия должна сохраняться, что обеспечивается переходом электрона в более высокое энергетическое состояние, то есть он покидает основное состояние с наименьшим уровнем энергии и переходит на более высокий энергетический уровень. Однако этот более высокий энергетический уровень не может иметьпроизвольное значение энергии, поскольку энергетические уровни частицы в ящике (и в молекулах) квантуются. Самое низкое энергетическое состояние над основным уровнем соответствует квантовому числу n=2. Это состояние называется первым возбуждённым. Электрон возбуждается при поглощении фотона и переходит из основного состояния в первое возбуждённое. Энергия первого возбуждённого состояния (n=2) равна

E=4∙h²/8∙m∙L².

Энергия должна сохраняться. Это верно для классической механики и остаётся верным в квантовой механике. Вначале электрон находился в основном состоянии. Затем, после поглощения фотона, перешёл в возбуждённое состояние. Следовательно, для того чтобы соблюдался закон сохранения, энергия фотона должна быть равна разности между энергией возбуждённого состояния электрона и энергией его основного состояния. Только фотон с такой энергией может быть поглощён данной системой. Энергия фотона определяется длиной волны света. Следовательно, поглощаться может свет только некоторых определённых цветов.

Рисунок 8.7 иллюстрирует поглощение фотона. Стрелки показывают два разрешённых пути, по которым может поглотиться фотон. Их называют переходами. На рисунке отражены переходы из n=1 в n=2 и из n=1 в n=3. Чтобы фотон был поглощён, его энергия должна быть равна разности энергий двух квантовых уровней. Если энергия фотона не совпадает с разностью энергий двух квантовых уровней, он не может поглотиться.

Разность энергий ∆E между энергетическим уровням перового возбуждённого состояния (n=2) и энергетическим уровнем основного состояния (n=1) равна

∆E=(4∙h²/8∙m∙L²)−(h²/8∙m∙L²),

∆E=3∙h²/8∙m∙L².

Это энергия, которую должен иметь фотон, чтобы заставить электрон совершить переход из основного состояния в первое возбуждённое. Можно воспользоваться соотношением Планка E=h∙ν для энергии фотона, чтобы убедиться в том, что энергии ∆E соответствует определённая частота света. Кроме того, поскольку произведение длины волны и частоты равно скорости света λ∙ν=c, можно найти длину волны (цвет) того света, который будет испытывать поглощение.

Рис. 8.7.Энергетические уровни частицы в ящике. n — квантовое число, энергия E выражена в единицах h²/8∙m∙L². Стрелками обозначено поглощение фотонов, которое может привести к переходу электрона с низшего энергетического уровня n=1 на более высокие энергетические уровни n=2, n=3 и т. д. Чтобы фотон был поглощён, его энергия должна совпадать с разностью энергий квантовых уровней

Цвет фруктов

Подставим в формулы численные значения постоянной Планка h=6,6∙10⁻³⁴ Дж∙cек и массы электрона m_e=9,1∙10⁻³¹ кг. В качестве длины ящика L примем средний размер молекулы: L=0,8∙10⁻⁹ м (0,8 нанометра, 0,8 нм). Тогда

ΔE= 3∙(6,6∙10⁻³⁴)² / 8∙(9,1∙10⁻³¹)∙(0,8∙10⁻⁹)²= 2,8∙10⁻¹⁹ Дж.

Разделив полученное значение энергии на h, получим частоту ν=4,25∙10¹⁴ Гц, которая соответствует длине волны поглощаемого света λ=7,06∙10⁻⁷ = 706 нм. Свет с длиной 706 нм находится у самого красного края видимого спектра. Что случится, если размер ящика (молекулы) будет меньше и составит, допустим, 0,7 нм, а не 0,8 нм? Энергия поглощаемого света при этом будет больше, а значит, с уменьшением размеров ящика длина волны поглощаемого света становится меньше. Поглощаемая энергия обратно пропорциональна L² (L² находится в знаменателе). Это означает, что с уменьшением размера ящика интервал между энергетическими уровнями увеличивается, а разность энергий возрастает как квадрат длины ящика. Таким образом, для ящика длиной 0,7 нм поглощаемая длина волны составит λ=540 нм, что соответствует зелёному свету. Если же размер ящика будет ещё меньше, допустим 0,6 нм, то λ=397 нм, и это самый голубой край спектра света, видимого невооружённым глазом.

Эти результаты в общих чертах справедливы и для молекул, хотя при этом необходимо принимать в расчёт множество тонкостей. Однако для ряда молекул, имеющих в целом сходную структуру (типы атомов и т. п.), чем крупнее молекула, тем более красный свет она поглощает. Наши результаты, полученные для частицы в ящике, демонстрируют на сугубо качественном уровне, почему вещи бывают разного цвета. Маленькие молекулы поглощают свет в ультрафиолетовой части спектра. Мы не видим ультрафиолет, так что поглощение малыми молекулами не влияет на цвет. Мы видим те цвета, которые содержатся в свете, отражённом от объекта. Цвета, которые соответствуют поглощаемым длинам волн, не отражаются. Крупные молекулы поглощают в видимой части спектра, и именно молекулярное поглощение придаёт вещам их цвет.

Вишня имеет красный цвет, а черника — синий, потому что в них содержатся различные молекулы, которые сильно поглощают волны разной длины, соответствующие разным цветам света. В этих молекулах есть квантованные электронные переходы. За счёт переходов из своих основных электронных состояний в возбуждённые состояния они могут поглощать световые волны только таких длин, которые определяются их квантованными энергетическими уровнями. В случае частицы в ящике значения энергии переходов для электрона определяются исключительно длиной ящика и массой электрона. Для молекул квантование энергии переходов, а значит длины волн и цвета, определяется как размерами молекул, так и особенностями их строения, то есть формой молекул, типами атомов, из которых они состоят, и тем, как атомы расположены.

Красители — это молекулы, обладающие свойством поглощать строго определённые волны видимого диапазона спектра. Красители используются для придания различного цвета нашей одежде. Ярко окрашенные растения, зелёные листья и красные розы содержат большой набор молекул разных размеров и форм, которые поглощают свет в определённых участках спектра. Именно размеры и формы этих молекул придают растениям их замечательные цвета. Если молекулы интенсивно поглощают зелёный и красный цвета, отражаться от объекта будет голубой цвет, и он будет выглядеть голубым. Если выраженно поглощаются голубой и зелёный, то отражаться будет преимущественно красный свет и объект будет выглядеть красным. То, какие цвета будут поглощаться объектом, определяется квантованием энергетических уровней в его молекулах.

В повседневной жизни мы постоянно видим различные цвета. Цвет — одно из множества свойств предметов, объясняемых только на основе квантовой механики. Однако есть много других подобных свойств. Например, когда вы включаете электрообогреватель, его спираль нагревается. Почему при прохождении электрического тока по металлу вырабатывается тепло (см. главу 19)? Это ещё одно повседневное квантовое явление. Почему углекислый газ является парниковым (см. главу 17)? Что такое транс-жиры (см. главу 16)? Для того чтобы понять свойства таких систем, необходимо погрузиться в квантовую механику молекулярных структур. В следующих главах мы рассмотрим квантовое описание атомов и молекул и применим его к ряду широко известных ситуаций и задач. Необходимый аппарат для понимания свойств атомов и молекул разрабатывается в главах с 9-й по 14-ю. Эти главы содержат огромное количество интересной информации о поведении атомов и молекул, которая позволяет перекинуть мост от общих идей квантовой теории, с которыми мы до сих пор знакомились, к пониманию множества окружающих нас явлений.

9. Атом водорода: история

В главе 8 мы обсудили задачу о частице в ящике. Мы представили себе электрон, запертый в очень маленьком одномерном ящике, изображённом на рис. 8.1. Задача о частице в ящике полезна тем, что используемый в ней математический аппарат достаточно прост, чтобы, приложив небольшие усилия, найти квантованные энергетические уровни. Нами была получена формула, которая показывает, что энергетические состояния частицы в ящике представляют собой дискретные ступени, зависящие от квантового числа n, которое принимает целые значения, начиная с единицы. Отмечалось, однако, что это крайне искусственный пример удержания квантовой частицы. В природе не бывает по-настоящему одномерных систем. Кроме того, стенки ящика бесконечно высоки и совершенно непроницаемы. Это тоже физически неосуществимо. Как говорилось при обсуждении фотоэлектрического эффекта в главе 4, если энергии фотона хватает на преодоление энергии связи электронов с атомами в куске металла, то взаимодействие такого фотона с первоначально связанным электроном может выбить его из металла (см. рис. 4.3).

Тем не менее по ряду причин изучать частицу в ящике очень полезно. Во-первых, обнаруживается, что энергетические уровни квантуются (см. рис. 8.6). В противоположность классической механике, энергия, которой может обладать электрон, запертый в ящике размером с атом или молекулу, не является непрерывной величиной. Она может меняться только дискретными шагами. Фотон с подходящей энергией может возбудить электрон, переведя его с одного энергетического уровня на другой (см. рис. 8.7). Энергия такого фотона должна совпадать с разностью между энергией того уровня, на который он переходит, и энергией того уровня, который он покидает. Однако в отличие от реальных систем никакая энергия не способна выбить электрон из ящика, поскольку его стенки бесконечно высоки. Это способ сказать, что электрон имел бы бесконечно большую энергию за пределами ящика. Ящик представляет собой бесконечно глубокий колодец, и электрон сидит в нём как в ловушке; никакая конечная энергия не способна преодолеть бесконечную энергию связи.

Другая важная особенность частицы в ящике связана с природой волновых функций. Волновые функции — это волны амплитуды вероятности, связанные с местоположением электрона в ящике (см. рис. 8.4). Квадраты этих волновых функций (см. рис. 8.5) характеризуют вероятность обнаружения электрона в той или иной области пространства. У волн амплитуды вероятности есть узлы. С увеличением квантового числа количество этих узлов возрастает. Узлы — это места, где вероятность обнаружить частицу, например электрон, равна нулю.

Атомы, в отличие от одномерной частицы в ящике, — это реальные трёхмерные физические системы. Трёхмерность атомов приводит к существенным отличиям от одномерной частицы, но, как будет показано в главе 10, некоторые самые важные особенности квантовомеханического описания атомов качественно подобны результатам, полученным для частицы в ящике. У атомов есть квантованные энергетические уровни. Они обладают волновыми функциями с узлами, количество которых возрастает с увеличением квантового числа. Однако много в них устроено совсем по-другому. Например, квантовым состояниям атомов соответствует несколько квантовых чисел, а поскольку атомы трёхмерны, их волновые функции представляют собой трёхмерные структуры^{11}. Эти особенности атомов будут обсуждаться в главе 10 на примере простейшего атома — водорода. Но сначала давайте познакомимся с некоторыми ранними наблюдениями, показавшими, что классическая механика не способна описывать атомы.

Спектр солнечного черноте́льного излучения

Мы уже говорили о спектроскопии — экспериментальном методе, который состоит в получении спектра света, испускаемого системой или поглощаемого ею. Спектр — это просто запись интенсивности света разных цветов. Для его получения измеряется количество света каждой длины волны (цвета). Говоря о цветах, мы имеем в виду не только те цвета, которые мы способны видеть, то есть не только видимый спектр, но и более длинные инфракрасные волны (с меньшей энергией) и более короткие ультрафиолетовые (с большей энергией)^{12}. Система может представлять собой контейнер, наполненный молекулярным газом, лист растения или молекулы в жидкости вроде тех, что придают вину красный цвет. Мы используем сложные молекулы красителей, чтобы придать цвет одежде, поскольку размер и строение молекул определяют, какие длины волн света будут поглощаться.

В главе 4 коротко говорилось об излучении чёрного тела. Нагретые объекты испускают свет. Очень горячий кусок металла будет светиться красным. Так происходит с нагревательными элементами электрической печи. С повышением температуры цвет будет смещаться по спектру в голубую сторону. Мы уже упоминали о том, что звёзды хорошо описываются как чёрные тела, и цвет звезды может служить для определения её температуры. Планк вывел формулу, которая описывает спектр чёрного тела при заданной температуре.

На рис. 9.1 представлен солнечный спектр, вычисленный по формуле Планка, который наилучшим образом согласуется с экспериментально измеренным спектром Солнца. Частота выражена числом волн, укладывающихся на одном сантиметре (см⁻¹). Умножение частоты (см⁻¹) на скорость света (3∙10¹⁰ см/сек) даёт частоту в герцах (Гц), привычных единицах измерения частоты. Сверху по оси абсцисс отложена длина волны в нанометрах (нм): 500 нм — это зелёный свет, 400 нм — ярко выраженный голубой, 666 нм — глубокий красный, 333 нм — ультрафиолетовое излучение, не видимое глазом, 1000 нм — также невидимое инфракрасное излучение. Эти длины волн можно обнаружить с помощью электронных фотодетекторов. Первоначально их регистрировали с помощью фотоплёнки. По вертикальной оси отложена интенсивность излучения. Она измеряется числом ватт (джоулей в секунду) энергии, приходящей на площадку в 1 квадратный метр в узком диапазоне частот 1 см⁻¹. Фактически этот график показывает, сколько энергии излучения конкретного цвета падает в секунду на один квадратный метр.

Рис. 9.1. Черноте́льный спектр Солнца, вычисленный по формуле Планка для теплового излучения горячего объекта. Эта кривая хорошо соответствует солнечному спектру, за исключением некоторых тонких деталей. По нижней оси отложены частоты, выраженные числом волн на 1 см (см. текст). По верхней оси отложена длина волны в нанометрах. Зелёный свет — это 500 нм, ярко выраженный голубой — 400 нм, глубокий красный — 666 нм. По вертикальной оси отложена интенсивность излучения (см. текст)

Форма спектра, изображённого на рис. 9.1, почти совпадает с реальным солнечным спектром. Расчётный спектр получен путём подгонки температуры в формуле Планка до наилучшего соответствия экспериментальному спектру. Температура, которая даёт такое соответствие, составляет 5780 K, где K — кельвины. Кельвин — это единица температуры по абсолютной шкале, разработанной Уильямом Томсоном, первым бароном Кельвином (лорд Кельвин, 1724–1907). Шкала Кельвина используется в физике и химии, поскольку нулевая отметка на этой шкале (0 K) имеет чётко определённый физический смысл. При 0 K прекращаются все движения атомов, связанные с кинетической энергией, то есть с теплом, с энергией движения частиц. Чтобы получить температуру в градусах Цельсия (°C), следует из температуры в кельвинах вычесть 273. Таким образом, по шкале Цельсия температура Солнца составляет 5507 °C.

Тёмные линии в солнечном спектре

Поразительно, что формула Планка, выведенная с опорой на первую квантовую идею о том, что энергия электронов, «осциллирующих» в металле, не является непрерывной, оказалась применимой к температуре звёзд. Расчётный спектр, изображённый на рис. 9.1, является непрерывным, поскольку горячий объект порождает непрерывное распределение цветов (энергии квантов света). Хотя экспериментальные данные в целом соответствуют кривой на рис. 9.1, на них также совершенно отчётливо проявляются детали, которые отсутствуют на черноте́льном спектре Солнца. На рис. 9.2 изображён солнечный спектр с тёмными линиями, отражающими нехватку света некоторых частот. Спектр, изображённый на рис. 9.1, соответствует излучению, испускаемому Солнцем. Тёмные линии — это узкие диапазоны длин волн, которые не доходят до Земли. Они называются линиями, или полосами, поглощения. Те же самые линии совершенно отчётливо видны в спектрах света, приходящего от других звёзд.

Длины волн, соответствующие тёмным линиям в солнечном спектре, можно наблюдать как отдельные цвета дуговой лампы, заполненной водородом. Водородная дуговая, или газоразрядная, лампа представляет собой заполненный водородом герметичный стеклянный цилиндр с электродами на концах. Когда достаточно высокий положительный электрический потенциал подаётся на один электрод, а отрицательный — на другой, в лампе возникает электрическая дуга, подобная маленькой непрерывно бьющей молнии. Цвета, или длины волн, в диапазоне видимого света, испускаемые лампой, соответствуют длинам волн тёмных линий спектра на рис. 9.2.

Рис. 9.2. Видимая часть солнечного спектра. Непрерывная последовательность цветов — это черноте́льный спектр. Тёмные линии, или полосы, — это цвета, соответствующие длинам волн, которые не доходят до Земли, так что они выглядят отсутствующими цветами в солнечном спектре. Длины волн этих линий отложены на шкале вдоль спектра в нанометрах (1 нм = 10⁻⁹ м)

Спектральные линии водорода

Первая попытка объяснить линейчатый спектр водорода в видимом диапазоне была предпринята в 1885 году школьным учителем и математиком Иоганном Бальмером (1825–1898). Бальмер заметил, что частоты f этих линий в видимой части спектра можно описать формулой

f~(1/2²)−(1/n²).

Символ ~ означает пропорциональность, то есть указывает на наличие постоянного множителя, о котором говорится ниже. В этом уравнении n — целое число больше 2, то есть 3, 4, 5 и т. д.

Эти линии в видимой части спектра называются бальмеровской серией. Позднее были открыты линии в ультрафиолетовой и инфракрасной частях спектра. Их назвали сериями Лаймана и Пашена соответственно в честь их первооткрывателей — американского физика и спектроскописта Теодора Лаймана (1874–1954) и немецкого физика Луиса Карла Генриха Фридриха Пашена (1865–1947). В 1888 году шведский физик и спектроскопист Йоханнес Ридберг (1854–1919) опубликовал формулу, которая описывала все спектральные линии, видимые в излучении водородной дуговой лампы и в спектрах поглощения солнечного и звёздного света. Формула Ридберга для частоты спектральных линий водорода имеет вид

f=R_H∙[(1/n₁²)−(1/n₂²)],

где n₁ — целые числа, начиная с 1, а n₂ — другие целые числа, которые должны быть больше n₁. Значение n₁=1 даёт лаймановскую серию, n₁=2 — бальмеровскую, n₁=3 — серию Пашена.

Константа R_H называется постоянной Ридберга для атома водорода. Её значение составляет R_H=109677,6 см⁻¹ и выражено числом волн (см⁻¹). При использовании этого значения в формуле Ридберга частоты спектральных линий, определяемые целыми числами n₁ и n₂, выражаются волновыми числами. Для перевода результата в герцы надо умножить полученное значение на скорость света, то есть на 3∙10¹⁰ см/сек. Чтобы найти длину волны спектральной линии, надо взять величину, обратную частоте, выраженной числом волн, то есть разделить единицу на частоту, выраженную числом волн. Например, если n₁=2, а n₂=3, то

f=R_H∙[(1/2²)−(1/3²)] = R_H∙[(1/4)−(1/9)] = 1,52∙10⁴ см⁻¹

представляет собой частоту, выраженную числом волн. Обратная величина для этого числа составляет 6,56∙10⁻⁵ см = 656∙10⁻⁹ м = = 656 нм. Таким образом, длина волны составляет 656 нм — это красная линия в серии Бальмера, изображённой на рис. 9.2.

При обсуждении рис. 8.7 уже говорилось о дискретности оптических переходов между квантовыми энергетическими уровнями для частицы в ящике. На рис. 8.7 показаны переходы между состояниями частицы в ящике, при которых n=1 превращается в n=2 и n=1 превращается в n=3. В связи с этим не должен стать большим сюрпризом тот факт, что оптические переходы в атоме водорода могут соответствовать дискретному набору частот, которые зависят от целых чисел. Однако в 1888 году, когда была получена формула Ридберга, оставалось ещё 12 лет до появления идеи квантования энергетических уровней, с помощью которой Планк объяснил черноте́льное излучение, и 37 лет до того, как в 1925 году сформировалась полноценная квантовая теория. Различные серии спектральных линий, энергии которых связаны посредством целых чисел по формуле Ридберга, можно понять как оптические переходы между дискретными энергетическими уровнями, связанные с атомом водорода.

Рис. 9.3. Схемы некоторых энергетических уровней, порождающих серии Лаймана и Бальмера линий эмиссии водорода. Стрелки, направленные вниз, показывают, как свет испускается водородом, например, в дуговой лампе. При поглощении, дающем тёмные линии на рис. 9.2, стрелки были бы направлены вверх. Интервалы между уровнями показаны условно, а не в масштабе

Некоторые энергетические уровни, благодаря которым возникают серии Лаймана и Бальмера, изображены на рис. 9.3. Здесь стрелки, направленные вниз, соответствуют эмиссионным линиям, которые наблюдаются у водородной дуговой лампы. Атом водорода, который первоначально находится на более высоком энергетическом уровне, со временем переходит на более низкий уровень. Энергия при этом сохраняется за счёт испускания фотона. Для сохранения энергии фотон должен нести энергию, равную разности между первоначальным, более высоким энергетическим уровнем и конечным уровнем с более низкой энергией. Наименьшее возможное значение n₁ в формуле Ридберга равно 1, а n₂ должно быть больше n₁. Стрелка, помеченная 2–1, соответствует излучению при переходе с уровня n=2 на уровень n=1.

Следующая по величине энергия излучения в лаймановской серии получается при переходе с уровня n=3 на уровень n=1. В формуле Ридберга следующее возможное значение для n₁ равно 2, а n₂ должно быть больше n₁. Поэтому наименьшая энергия линии излучения в серии Бальмера отмечена как 3–2. Когда атом водорода, находящийся на уровне n=3, переходит на уровень n=2, сохранение энергии обеспечивается испусканием фотона с длиной волны 656 нм. Когда свет падает на атомы водорода, происходит поглощение, которое можно было бы изобразить на той же диаграмме стрелками, направленными вверх.

Боровская теория атома водорода (не вполне совершенная)

Первое подробное описание энергетических уровней водорода было дано Нильсом Бором (1885–1962) в 1913 году. Бор получил Нобелевскую премию по физике в 1922 году

«за заслуги в изучении строения атома».

Созданная Бором теория атома водорода считается предвестницей квантовой теории. Бор добился большого прогресса — фактически он сумел точно вычислить энергетические уровни атома водорода, выведя формулу Ридберга и предсказав все спектральные линии водорода.

Бор также первым выдвинул две идеи, которыми мы уже пользовались. Он заявил, что атомная система может существовать только в некоторых состояниях, которые он называл «стационарными». Сегодня мы обычно называем их собственными состояниями энергии. Каждому из этих состояний соответствует чётко определённое значение энергии E. Переход из одного стационарного состояния в другое может произойти при поглощении и испускании света или другом способе потери или получения энергии системой, а количество этой энергии должно быть равно разности энергий данных двух состояний. Эта идея положена в основу схем, представленных на рис. 9.3 и 8.7, где стрелки изображают переходы между состояниями, происходящие при поглощении и испускании света.

Бор также выдвинул постулат, известный ныне как правило частот. Частота испускаемого или поглощаемого света при переходе от начального энергетического состояния E₁ к конечному E₂ равна разности их энергии, делённой на постоянную Планка:

ν=|E₁−E₂|/h,

где ν — частота, а h — постоянная Планка (h=6,6∙10⁻³⁴ Дж∙сек). Вертикальными линиями в формуле обозначена абсолютная величина. В случае поглощения E₁ меньше E₂, так что разность E₁−E₂ имеет отрицательное значение. Смысл абсолютной величины состоит в том, что в качестве результата берётся положительное значение, даже если разность получается отрицательной. Частота ν должна быть положительным числом. Умножив обе части формулы на h, получаем, что E — разность энергий между энергетическими уровнями (стационарными состояниями) — равна E=h∙ν, то есть даётся формулой Планка, которую использовал Эйнштейн для объяснения обсуждавшегося в главе 4 фотоэлектрического эффекта.

Что же представляет собой атом водорода и в чём недостаток метода, предложенного Бором? Атом водорода состоит из двух заряженных частиц: протона, несущего положительный заряд +1, и электрона, который имеет отрицательный заряд −1. Когда говорится о заряде, равном 1, это в действительности сокращённая запись для заряда одного протона. В стандартных физических единицах он равен 1,6∙10⁻¹⁹ Кл, где Кл — обозначение кулона, единицы измерения заряда. Эрнест Резерфорд (1871–1937) провёл в 1911 году эксперименты, которые показали, что атомы состоят из маленького тяжёлого положительно заряженного ядра и одного или более электронов вокруг него. Резерфорд получил Нобелевскую премию по химии в 1908 году

«за проведённые им исследования в области распада элементов в химии радиоактивных веществ».

Открытия Резерфорда в применении к атому водорода означают, что протон является ядром, а единственный электрон находится вне ядра. Даже ядро водорода, состоящее из одного протона, намного тяжелее электрона. Масса протона составляет m_p=1,67∙10⁻²⁷ кг, тогда как масса электрона равна всего лишь m_e=9,1∙10⁻³¹ кг. То есть протон весит примерно в 1836 раз больше, чем электрон.

В боровской модели водорода электрон обращается вокруг протона, как планета вокруг Солнца. В наинизшем энергетическом состоянии атома водорода (n=1) электрон движется вокруг протона по окружности. В более высоких энергетических состояниях орбита электрона с n больше 1 может принимать различные формы. Некоторые из них остаются окружностями, но другие оказываются эллипсами. С учётом сказанного в предыдущих главах эта картина электрона, обращающегося вокруг протона, должна немедленно вызвать срабатывание «тревожной сигнализации». В главе 6 обсуждался принцип неопределённости Гейзенберга. Мы знаем, что движение абсолютно малой частицы не может описываться классической траекторией. Для описания траектории необходимо знать положение и импульс частицы на протяжении всего времени движения. Однако принцип неопределённости Гейзенберга гласит, что невозможно одновременно и точно знать положение и импульс. В соответствии с соотношением неопределённости Δx∙Δp≥h/4π, где h — постоянная Планка. Абсолютно малые частицы описываются волнами амплитуды вероятности, а не траекториями. Конечно, в 1913 году, когда Бор выдвинул своё математическое описание атома водорода, природа абсолютно малых частиц была ещё неизвестна.

Ошибочность боровского подхода становится очевидной, когда он применяется к системам, отличным от атома водорода. Хотя он способен очень точно предсказать энергетические уровни, а тем самым и спектр атома водорода, он не позволяет сделать это для второго по простоте атома — гелия. Не может он предсказать и свойств простейшей молекулы, а именно молекулы водорода, которая состоит из двух атомов. Метод отбора не объясняет силу химической связи, которая удерживает вместе два атома водорода в молекуле. Тем не менее Бор сделал огромный шаг в правильном направлении, а ошибки его подхода в конечном счёте привели к созданию истинной квантовой теории в 1925 году.

10. Атом водорода: квантовая теория

В 1925 году Шрёдингер и Гейзенберг независимо друг от друга разработали квантовую теорию. Созданные ими два формализма различались с математической точки зрения, но оба были точными и стали основанием для современной квантовой теории. Примерно в то же время Дирак также сделал крупный вклад в науку. Во-первых, он предложил объединённый взгляд на квантовую теорию, в рамках которого показал, что теории Шрёдингера и Гейзенберга, несмотря на математические различия, являются эквивалентными представлениями квантовой механики. Кроме того, он разработал квантовую теорию атома водорода, совместимую с теорией относительности Эйнштейна.

Для описания атомов и молекул обычно используется формулировка Шрёдингера. Поэтому в большинстве случаев мы будем начинать с атома водорода, а затем переходить к более крупным атомам и молекулам, опираясь при этом на понятия и язык, соответствующие шрёдингеровскому подходу.

Уравнение Шрёдингера

Мы использовали очень простой, но корректный математический метод определения энергетических уровней и волновых функций частицы в ящике, но этот метод не является универсальным. Например, он не может использоваться для определения энергетических уровней и волновых функций атома водорода. На самом деле используемые нами понятия, такие как волновые функции и волны амплитуды вероятности, пришли из шрёдингеровской формулировки квантовой механики. Уравнение Шрёдингера — это сложное дифференциальное уравнение в трёх измерениях. Мы не будем касаться математического аппарата, позволяющего решать уравнение Шрёдингера для атома водорода или других атомов и молекул. Однако мы воспользуемся многими полученными с его помощью результатами, чтобы ознакомиться с устройством атомов и молекул, начиная с атома водорода.

Решение задачи об атоме водорода с помощью уравнения Шрёдингера особенно важно, потому что оно является точным. Атом водорода — это пример так называемой задачи двух тел. В ней рассматриваются лишь две частицы: протон и электрон. Следующим по простоте является атом гелия, состоящий из ядра с зарядом +2 и двух отрицательно заряженных электронов. Это задача трёх тел, которую невозможно решить точно. Задача определения орбиты Земли, обращающейся вокруг Солнца, с Луной, обращающейся вокруг Земли, не имеет точного решения в классической механике. Однако и в квантовой, и в классической механике есть очень изощрённые приближённые методы, позволяющие с необходимой точностью решать задачи, которые нельзя решить аналитически. То, что метод является приближённым, не означает, что он грубый. И всё же поскольку задачу об атоме водорода в квантовой механике можно решить точно, она является важной отправной точкой для понимания более сложных атомов и молекул.

Что уравнение Шрёдингера говорит нам о водороде

Что даёт нам решение уравнения Шрёдингера для атома водорода? Оно позволяет определить энергетические уровни атома водорода и волновые функции, связанные с каждым состоянием этого атома. Волновые функции — это трёхмерные волны амплитуды вероятности, которые описывают области пространства, где может быть обнаружен электрон. Решение Шрёдингера для задачи об атоме водорода даёт значения энергетических уровней, совместимые с эмпирически полученной формулой Ридберга:

E_n=−R_H/n²,

где n — главное квантовое число. Это целочисленная величина, которая может принимать значения ≥1, то есть быть больше либо равной единице.

Разница в энергии между любыми двумя энергетическими уровнями даётся формулой Ридберга. Однако в решении Шрёдингера величина R_H не является эмпирическим параметром. Решая эту задачу, Шрёдингер нашёл, что постоянная Ридберга связана с фундаментальными постоянными формулой

R_H=−μ∙e⁴/8∙ε₀²∙h².

Здесь h — постоянная Планка;

e — заряд электрона;

ε₀=8,54∙10⁻¹² Кл²/Дж∙м — постоянная, называемая диэлектрической проницаемостью вакуума;

μ — приведённая масса протона и электрона:

μ=m_p∙m_e/(m_p+m_e),

где m_p и m_e — массы протона и электрона соответственно. Значения заряда и массы электрона и протона уже приводились выше.

Если Ридберг получил экспериментальные данные и вывел эмпирическую формулу, описывающую линии спектра атома водорода, то в решении Шрёдингера для задачи об атоме водорода квантовая теория используется совершенно иным образом. Мы немного задержимся, чтобы восхититься триумфом квантовой теории, достигнутым в 1925 году. При выводе Шрёдингером энергетических уровней атома водорода не использовалось никаких подгоночных параметров. Все необходимые константы — это фундаментальные свойства частиц и электростатического взаимодействия, благодаря которому отрицательно заряженный электрон притягивается к положительно заряженному протону. Шрёдингер не обращался к экспериментальным данным, чтобы подогнать константу R_H для лучшего совпадение с ними. Он создал теоретический формализм и применил его к атому водорода. Его теория в точности воспроизвела результаты экспериментальных наблюдений — спектральные линии атома водорода, опираясь только на фундаментальные постоянные.

В отличие от теории Бора уравнение Шрёдингера с успехом применялось к огромному числу других задач, включая атомы, отличные от водорода, а также небольшие и крупные молекулы. Как уже упоминалось, для систем крупнее атома водорода, то есть для атомов и молекул, состоящих более чем из двух частиц, уравнение Шрёдингера нельзя решить точно. Однако было разработано множество эффективных приближённых методов решения уравнения Шрёдингера для атомов, молекул и других типов квантовомеханических систем. Благодаря развитию компьютеров и их огромной вычислительной мощности стало возможно решать уравнение Шрёдингера для очень больших и сложных молекул. В следующих главах рассказывается о формах молекул. Решение уравнения Шрёдингера для молекулы даёт её энергетические уровни и волновые функции. Волновые функции содержат информацию, необходимую для определения формы молекул.

Четыре квантовых числа

Энергии различных состояний атома водорода описываются единственным квантовым числом n. Однако в действительности есть четыре квантовых числа, связанных с электронами в атомах. Они появляются при решении задачи об атоме водорода в рамках квантовой теории. Одно из них существенно лишь для атомов и молекул, имеющих более одного электрона. В этом смысле атом водорода является частным случаем, поскольку в нём всего один электрон. Для атома водорода, помимо главного квантового числа n, есть ещё два квантовых числа — l и m. Число l называется орбитальным квантовым числом, m — магнитным квантовым числом. От них в сочетании с квантовым числом n зависит, сколько различных состояний связано с конкретным значением энергии, они также определяют форму волновых функций. Четвёртое квантовое число обозначается s. Его называют спи́новым квантовым числом.

Когда Бор решал задачу об атоме водорода, в рамках старой квантовой теории считалось, что электрон движется по орбитам, имеющим разные формы и значения энергии. Корректное квантовое решение Шрёдингера для атома водорода даёт энергетические уровни и волновые функции, которые соответствуют боровским орбитам и называются «орбиталями». Обсуждая атомы и молекулы, мы часто используем термины «волновая функция» и «орбиталь» в качестве синонимов. Орбитали являются волнами амплитуды вероятности, которые подчиняются принципу неопределённости Гейзенберга, чем отличаются от боровских орбит.

Как уже отмечалось выше, главное квантовое число n может принимать целочисленные значения n≥1, то есть 1, 2, 3, 4 и так далее, а l может принимать значения от 0 до n−1 с целым шагом. Число m может иметь значения от l до −l с целым шагом. Наконец, число s может принимать только два значения: +½ и −½. Сводка возможных значений квантовых чисел приведена в таблице ниже.

По историческим причинам состояния с различными значениями квантового числа l имеют индивидуальные обозначения. Состояние l=0 называется s-орбиталью. При l=1 говорят о p-орбитали, при l=2 — это d-орбиталь, а при l=3 — f-орбиталь. Для обсуждения всех атомов нам не понадобится заходить далее f-орбиталей, то есть l=3. Как показано ниже, различные орбитали имеют разные формы.

Поскольку энергии состояний (орбиталей) атома водорода зависят только от квантового числа n, для n>1 имеется более одного состояния с одинаковой энергией. Для n=1 имеем l=0 и m=0 (см. таблицу), поэтому существует единственная орбиталь с n=1. Для этой орбитали l=0, так что её обозначают как 1s-орбиталь. Для n=2 число l может быть равно 0, что даёт 2s-орбиталь. Однако для n=2 число l также может равняться 1. При l=1 число m может быть равно 1, 0 или −1 (см. таблицу). При l=1 — это p-орбиталь, причём существуют три разные p-орбитали, обозначаемые 2p₁, 2p₀ и 2p₋₁. Здесь 2 — это главное квантовое число n, p означает l=1, а три индекса— это три возможных значения m. Таким образом, для n=2 существует четыре различных состояния.

Если n=3, то l может быть равно нулю, что даёт 3s-орбиталь. Также l может быть равно 1, что при m = 1, 0 и −1 даёт орбитали 3p₁, 3p₀, и 3p₋₁. Кроме того, l может быть равно 2. Для l=2 число m может иметь значения 2, 1, 0, −1 и −2. Это d-орбитали: 3d₂, 3d₁, 3d₀, 3d₋₁ и 3d₋₂. Всего имеется пять d-орбиталей. Таким образом, для n=3 имеется девять различных состояний: одна s-орбиталь, три p-орбитали и пять d-орбиталей. Когда n=4, есть 4s-орбиталь, три различные 4p-орбитали (4p₁, 4p₀ и 4p₋₁), пять различных 4d-орбиталей (4d₂, 4d₁, 4d₀, 4d₋₁ и 4d₋₂). Дополнительно имеется семь f-орбиталей: 4f₃, 4f₂, 4f₁, 4f₀, 4f₋₁, 4f₋₂ и 4f₋₃. Таким образом, для n=4 имеется в общей сложности 16 состояний: одна s-орбиталь, три p-орбитали, пять d-орбиталей и семь f-орбиталей.

Как уже говорилось, каждая из этих орбиталей имеет свою форму. Довольно часто орбитали называют в соответствии с их формой. Например, три различных 2p-орбитали, вместо того чтобы обозначать их 2p₁, 2p₀ и 2p₋₁, называют 2p_x, 2p_z и 2p_y. Связь между этими индексами и формами прояснится, когда мы познакомимся с соответствующими формами.

Энергетические уровни атома водорода

На рис. 10.1 представлена диаграмма энергетических уровней атома водорода. Изображены уровни с n от 1 до 5. Для удобства восприятия масштаб интервалов не соблюдается, но, как и показано, с увеличением n интервал между уровнями становится меньше. Также с увеличением n возрастает число различных состояний (орбиталей), соответствующих конкретному значению n. Водород — это особый случай, поскольку у него имеется лишь один электрон. Для водорода все орбитали с одинаковым значением n обладают равной энергией. В следующей главе будет объяснено, что в атомах с несколькими электронами орбитали с разными значениями l при одном и том же n обладают разными энергиями.

Рис. 10.1. Диаграмма энергетических уровней водорода. Изображены первые пять энергетических уровней. Для удобства восприятия масштаб интервалов между уровнями не соблюдается. Энергия зависит только от главного квантового числа n. Показано количество орбиталей каждого типа. При n=4 имеется одна s-орбиталь, три разные p-орбитали, пять разных d-орбиталей и семь разных f-орбиталей^{13}. Диаграмму можно продолжить для n=6. Различные уровни иногда называют оболочками

s-орбитали атома водорода

Хотя значения энергии в атоме водорода зависят только от главного квантового числа n, квантовые числа l и m тоже играют важную роль. Они определяют форму орбиталей и другие свойства, присущие атому водорода. Например, квантовое число m называется магнитным квантовым числом. Три 2p-орбитали (2p₁, 2p₀ и 2p₋₁) различаются значениями квантового числа m. Когда атом водорода помещают в магнитное поле, энергии этих трёх орбиталей перестают быть одинаковыми.

Издиаграммы энергетических уровней, вычисленных с помощью уравнения Шрёдингера (см. рис. 10.1), становится ясно, как возникает эмпирическая диаграмма, представленная на рис. 9.3. Оптические переходы, видимые как линии в спектре атома водорода и описываемые формулой Ридберга, — это переходы между энергетическими уровнями атома водорода, энергии которых вычисляются на основе квантовой теории без каких-либо подгоночных параметров.

Как уже упоминалось, квантовые числа n, l и m вместе определяют формы волновых функций. Для s-орбиталей l=0. Это означает, что электрон не имеет углового момента^{14} в своём движении относительно ядра атома. Все направления выглядят равноценными, так что s-орбитали — это сферически симметричные трёхмерные волны амплитуды вероятности. На рис. 10.2 схематически показаны орбитали (волны амплитуды вероятности) 1s, 2s и 3s. Более тёмный тон означает бо́льшую вероятность обнаружить электрон на соответствующем расстоянии от центра. Расстояния, на которых вероятности достигают максимума, показаны сплошными окружностями. Середины белых областей внутри орбиталей 2s и 3s (пунктирные окружности) — это узлы, то есть области, где вероятность обнаружить электрон обращается в нуль. При переходе от 1s к 2s и 3s размеры орбиталей значительно возрастают. С увеличением квантового числа n повышается вероятность обнаружить электрон вдали от ядра.

Рис. 10.2.Двумерные представления орбиталей 1s, 2s и 3s. В действительности они сферические. Более тёмный тон соответствует более высокой вероятности обнаружения электрона. Сплошными окружностями обозначены максимальные значения этой вероятности. Пунктирные окружности — это узлы, где данная вероятность обращается в нуль. При данном способе изображения орбитали имеют довольно чёткую внешнюю границу. Орбитали — это волны, которые становятся очень малыми на больших расстояниях, но обращаются в нуль лишь тогда, когда расстояние от центра стремится к бесконечности

Увеличение размера орбиталей — одна из причин того, что энергия возрастает с увеличением квантового числа n. Формула для энергетических уровней атома водорода начинается со знака «минус»: E_n=−R_H/n². Принято считать, что более низкая энергия — это бо́льшая по абсолютной величине отрицательная энергия. Атом водорода состоит из протона и электрона, притягивающихся друг к другу в результате кулоновского, то есть электростатического, взаимодействия. Противоположные заряды притягиваются. Протон — это положительно заряженная частица, а электрон заряжен отрицательно. Когда протон и электрон разнесены бесконечно далеко, они не ощущают влияния друг друга. Взаимодействия между ними из-за большого расстояния нет. Система имеет нулевую энергию, когда её частицы разнесены на бесконечно большое расстояние.

Взаимодействие электрона и протона усиливается по мере того, как они сближаются. Энергия системы убывает, становясь всё более отрицательной. На орбитали 2s электрон в среднем находится дальше от протона, чем на орбитали 1s, на орбитали 3s электрон в среднем ещё дальше от протона. Это видно на рис. 10.2. С увеличением квантового числа энергия выражается всё меньшими отрицательными числами. При больших значениях n требуется меньше энергии, чтобы разделить электрон и протон, то есть ионизировать атом. Ионизация — это процесс отрыва электрона от атома, так что они более не связаны друг с другом. При n=1 для ионизации атома требуется энергия R_H. Её нужно передать атому, чтобы превзойти энергию связи, равную — R_H. При n=2 энергия, требуемая для ионизации атома водорода, составляет всего R_H/4, а при n=3 необходимая энергия ещё меньше и составляет R_H/9.

Пространственное распределение s-орбиталей

Чтобы лучше представить себе пространственное распределение вероятности обнаружить электрон в определённом положении, полезно построить для волновых функций два типа графиков. Один из них — это просто график волновой функции в зависимости от расстояния до ядра. Это полезный график, но кое в чём он вводит в заблуждение. Второй тип графика называют радиальным распределением функции, и мы вкратце его опишем.

На рис. 10.3 представлен график волновой функции Ψ(r) в зависимости от расстояния до протона, который находится в центре атома. График этого типа показывает амплитуду вероятности обнаружить электрон вдоль одной прямой линии, уходящей радиально от центра. Значение r отсчитывается от тёмного центра распределения электрона на рис. 10.2 вправо в горизонтальном направлении. На рис. 10.3 видно, что вероятность обнаружить электрон быстро убывает вдоль отдельно взятой прямой и приближается к нулю, когда расстояние от ядра достигает 3 Å.

Рис. 10.3. График волновой функции Ψ(r) для орбиталей 1s в зависимости от расстояния r до протона. Значение Ψ(r) пропорционально вероятности обнаружить электрон вдоль линии, радиально уходящей от центра атома. Расстояние r выражено в ангстремах (1 Å = 10⁻¹⁰ м)

Проблема с графиком того типа, который представлен на рис. 10.3, состоит в том, что он не учитывает трёхмерную природу атома. Рассматривая 1s-орбиталь на рис. 10.2, мы понимаем, что можно обнаружить электрон на некотором расстоянии от центра, двигаясь не только вдоль линии, направленной вправо, но и вдоль линии, направленной влево, вверх или вниз. Можно также сдвинуться в любом диагональном направлении на расстояние r и получить ту же самую вероятность обнаружить электрон. Поскольку атом трёхмерен, можно также выйти из плоскости страницы и тоже обнаружить электрон. Если нужно знать вероятность обнаружения электрона на определённом расстоянии r от протона, то следует произвести суммирование по всем таким радиальным направлениям.

В действительности вопрос состоит в том, какова вероятность обнаружить электрон на некотором расстоянии от ядра, если сложить все возможные направления. Можно сформулировать этот вопрос иначе: какова вероятность обнаружить электрон в тонком сферическом слое радиусом r? Поскольку с увеличением r объём этого тонкого сферического слоя возрастает, то на некоторых расстояниях это нивелирует тот факт, что волновая функция убывает. Чтобы понять роль этого тонкого сферического слоя, рассмотрим ряд пустых резиновых мячей с одинаковой толщиной оболочки. Мяч маленького радиуса (r) будет содержать меньше резины, чем мяч большого радиуса. Если же вы просто пойдёте по одной прямой линии от центра мяча и, добравшись до его оболочки, поинтересуетесь толщиной резины, то она не будет зависеть от радиуса мяча. Ясно, однако, что в оболочке большого мяча содержится больше резины, чем в оболочке маленького.

Площадь поверхности сферы составляет 4π∙r², где r — радиус сферы. Умножив эту величину на толщину оболочки, вы получите объём резины в мяче. Теперь ясно, что большой мяч содержит намного больше резины в своей оболочке, чем маленький. Если удвоить радиус, количество резины увеличится в 4 раза. Другой важный факт: когда r стремится к нулю, количество резины в мяче тоже стремится к нулю, поскольку к нулю стремится площадь поверхности 4π∙r². Спрашивать, находится ли электрон на расстояние r от ядра, — это всё равно что спрашивать, сколько резины содержится в оболочке мяча радиусом r. Тут необходимо учитывать увеличение площади поверхности при увеличении радиуса.

Функция радиального распределения

Функция радиального распределения — это как раз то, что нужно для учёта трёхмерной природы атома. Чтобы по мере увеличения r учесть все направления поиска электрона, необходимо добавить множитель 4π∙r². Функция радиального распределения задаёт вероятность обнаружить электрон на расстоянии r от ядра для всех направлений. В главе 5 говорилось, что, согласно интерпретации волновой функции Бора, вероятность обнаружить частицу в некоторой области пространства пропорциональна квадрату абсолютного значения волновой функции. Сейчас мы хотим найти вероятность обнаружения электрона в тонком сферическом слое радиусом r. Это и будет функция радиального распределения, задаваемая формулой 4π∙r²∙|Ψ|². Вертикальные линии, как и прежде, обозначают абсолютную величину. Для функций, с которыми мы имеем дело, потребуется лишь возвести в квадрат волновую функцию.

Рис. 10.4. График функции радиального распределения для 1s-орбитали в зависимости от расстояния r до протона. Функция радиального распределения — это вероятность обнаружить электрон в тонком сферическом слое на расстоянии r от протона. Функция радиального распределения учитывает тот факт, что электрон может быть найден в любом направлении от протона. Расстояние r измеряется в ангстремах (1 Å = 10⁻¹⁰ м)

На рис. 10.4 показана функция радиального распределения для 1s-состояния атома водорода.

Расстояние, на котором достигается максимальная вероятность, — это не центр атома, поскольку объём сферического слоя стремится к нулю, когда r обращается в нуль. Вертикальная линия показывает положение максимума распределения вероятности, который находится на отметке r = 0,529 Å. Это значение представляет особый интерес. В старой боровской квантовой теории атома водорода электрон в 1s-состоянии движется по круговой орбите радиусом 0,529 Å. Это расстояние называется радиусом Бора и обозначается a₀. Корректное квантовомеханическое описание атома водорода гласит, что электрон — это волна амплитуды вероятности с расстоянием максимальной вероятности, равным радиусу Бора a₀. Это не случайное совпадение. Радиус Бора в действительности является фундаментальной постоянной. Он определяется формулой

a₀=ε₀∙h²/π∙μ∙e²,

где все параметры те же, что и в выражении для постоянной Ридберга через фундаментальные постоянные. На самом деле энергетические уровни атома водорода можно выразить через радиус Бора следующим образом:

E_n=−e²/8π∙ε₀∙a₀∙n².

На рис. 10.5 и 10.6 представлены графики волновых функций (вверху) и функций радиального распределения (внизу) для орбиталей 2s и 3s. Волновая функция для 2s-орбитали имеет узел, то есть место, где она обращается в нуль. Об узлах мы говорили в связи с волновой функцией частицы в ящике (см. рис. 8.4). Вблизи узла вероятность обнаружить частицу, в данном случае электрон, равна нулю. Волновая функция состояния 2s начинается с положительного значения, пересекает нулевое значение в узле, расположенном на расстоянии, равном удвоенному радиусу Бора (2а₀), а затем становится отрицательной. Далее волновая функция спадает до нуля. На расстоянии 8 Å значение волновой функции уже очень мало́.

Рис. 10.5. Волновая функция (вверху) и функция радиального распределения (внизу) для 2s-орбитали атома водорода в зависимости от расстояния r до протона. Волновая функция начинается с положительного значения, проходит через узел чуть дальше точки 1 Å (2a₀) и затем спадает до нуля. Функция радиального распределения демонстрирует максимум вероятности обнаружения электрона на отметке 2,8 Å, причём наиболее вероятно найти его в интервале от 2 до 4 Å (см. рис. 10.2). Расстояние r измеряется в ангстремах (1 Å = 10⁻¹⁰ м)

Рис. 10.6. Волновая функция (вверху) и функция радиального распределения (внизу) для 3s-орбитали атома водорода в зависимости от расстояния r до протона. Волновая функция начинается с положительного значения, проходит через узел, становясь отрицательной, проходит через второй узел, вновь становясь положительной, и затем спадает до нуля. Функция радиального распределения показывает, что вероятность обнаружения электрона достигает максимума на отметке 7 Å, причём наиболее вероятно найти его в интервале от 5 до 11 Å (см. рис. 10.2). Расстояние r измеряется в ангстремах (1 Å = 10⁻¹⁰ м)

Как уже подробно говорилось, волновые функции — это волны амплитуды вероятности. Подобно другим волнам, они могут быть положительными и отрицательными. В нижней части рис. 10.5 показана функция радиального распределения для состояния 2s. Это вероятность обнаружить данный электрон на расстоянии r от ядра. Вероятности всегда имеют положительные значения, поскольку являются квадратами волновой функции, которые всегда положительны.

Волна может быть положительной или отрицательной, но имеющие смысл значения вероятности являются положительными числами или нулём. Функция радиального распределения показывает, что бо́льшая часть вероятности приходится на интервал от 2 до 4 Å; это также видно на рис. 10.2, но без количественного описания. Пик вероятности приходится на отметку приблизительно 2,8 Å.

Из рис. 10.6 видно, что волновая функция 3s-орбитали имеет два узла, то есть дважды пересекает ноль. В этом отношении волновые функции атома водорода подобны волновым функциям частицы в ящике (см. рис. 8.4). При n=1 узлов нет. При n=2 имеется узел. При n=3 имеется два узла. Число узлов для s-орбиталей равно n−1. Волновая функция 3s начинается с положительного значения, затем становится отрицательной, а потом вновь положительной. В конце концов она спадает до нуля, становясь очень малой за отметкой 16 Å. Функция радиального распределения для 3s-орбитали показывает, что область наибольшей вероятности обнаружить электрон находится относительно далеко от ядра. Пик вероятности расположен приблизительно на 7 Å, а на интервал от 5 до 11 Å приходится наибольшая вероятность найти электрон. Три функции радиального распределения, изображённые на рис. 10.4–10.6, дают количественное выражение для информации, схематически представленной на рис. 10.2. По мере увеличения главного квантового числа (n) s-орбитали становятся больше и количество узлов возрастает.

Формы p-орбиталей

Для 2s-орбитали n=2, l=0 и m=0. Однако при n=2 число l также может быть равно 1 и с ним могут быть связаны три значения m:m = 1, 0, −1. Эти три значения m соответствуют трём различным 2p-орбиталям. Они показаны на диаграмме энергетических уровней на рис. 10.1.

Рис. 10.7. Схематическое изображение трёх 2p-орбиталей атома водорода: 2p _z , 2p _y и 2p _x . У каждой из них имеется два лепестка: один положительный и один отрицательный. У каждой есть узловая плоскость, то есть плоскость, где вероятность обнаружить электрон равна нулю. Лепестки 2p _z -орбитали располагаются вдоль оси z, а узловой является плоскость xy, выделенная серым тоном. У 2p _y -орбитали лепестки расположены вдоль оси y, а основная плоскость — в плоскости xz. Лепестки 2p _x -орбитали лежат вдоль оси z, а узловая плоскость — это yz. Лепестки на этой схеме показывают, где находится область с максимальной амплитудой вероятности для электрона. Волны амплитуды вероятности плавно спадают к нулю вдали от ядра (протона), а не обрываются резко, как на этих диаграммах

Три разные 2p-орбитали схематически представлены на рис. 10.7. Как уже говорилось, 2p-орбитали с учётом их формы обычно обозначают 2p_z, 2p_y и 2p_x. Каждая из этих орбиталей имеет два лепестка — положительный и отрицательный. Какой лепесток считать положительным, а какой — отрицательным, не важно, но знак должен меняться, поскольку имеется узловая плоскость. Лепестки 2p_z-орбитали расположены вдоль оси z. Узловая плоскость (на рисунке показана серым тоном) — это плоскость xy (z=0). Вероятность обнаружить электрон на этой плоскости равна нулю. Знак волновой функции меняется при переходе через узел. У 2s-орбитали имеется радиальный узел. Это сферическая поверхность на определённом расстоянии от центра, представляющая собой узел. Каждая из p-орбиталей имеет узловую плоскость, то есть совокупность направлений (плоскость), где располагается узел. У 2p-орбиталей нет радиального узла, но у 3p-орбиталей в дополнение к узловой плоскости есть радиальный узел, а у 4p-орбиталей имеется два радиальных узла и т. д.

Лепестки 2p_y-орбитали направлены вдоль оси y, а её узловая плоскость — это xy. У 2p_x-орбитали лепестки направлены вдоль оси x, а узловой является плоскость yz. Приведённые на рис. 10.7 схематические изображения 2p-орбиталей подобны изображениям s-орбиталей на рис. 10.2. Рисунок 10.7 позволяет понять, в каких областях амплитуда вероятности для электрона велика. Однако важно понимать, что эти волны амплитуды вероятности плавно спадают с удалением от ядра. На рисунке лепестки обрываются резко, но волновые функции на больших расстояниях ведут себя подобно тому, как это показано на рис. 10.3 для 1s-орбитали. Тем не менее рис. 10.7 полезен для того, чтобы представить себе формы 2p-орбиталей. Эти формы окажутся очень важными, когда речь пойдёт о молекулярных связях и формах молекул.

Формы d-орбиталей

При n=3 число l может быть равно 0, что даёт 3s-орбиталь. Также l может быть равно 1, что при m = 1, 0, −1 даёт три различные 3p-орбитали. Кроме того, l может быть равно 2, что при m = 2, 1, 0, −1, −2 даёт пять различных 3d-орбиталей. Они показаны на диаграмме энергетических уровней (см. рис 10.1). На рис. 10.8 изображено пять различных 3d-орбиталей. Как и p-орбиталям, d-орбиталям часто дают названия, отражающие их форму, вместо того чтобы обозначать их квантовым числом m. Четыре из этих орбиталей имеют в целом одинаковую форму. У каждой имеется четыре лепестка и две узловые плоскости. Два из этих лепестков положительные, а другие два отрицательные. При пересечении узловой плоскости волновая функция меняет знак. Пятая орбиталь (d_x²) имеет другую форму, но у неё по-прежнему две узловые поверхности. Это конические поверхности, изображённые на диаграмме. Как и в случае с p-орбиталями, на рис. 10.8 тоном выделены области с наибольшей амплитудой вероятности обнаружения электрона. Эти волны амплитуды вероятности спадают к нулю с увеличением расстояния от ядра.

Рис. 10.8. Схематическое изображение пяти 3d-орбиталей атома водорода, обозначенных в соответствии с их формой. Каждая орбиталь имеет две узловые поверхности, а также положительные и отрицательные лепестки. На четырёх из них узловые поверхности имеют вид плоскостей, а на пятой — форму конусов. При пересечении узловых поверхностей волновая функция меняет знак. Лепестки на каждой диаграмме показывают, где расположены области наибольшей амплитуды вероятности для электрона. Четыре орбитали содержат по четыре лепестка каждая. Однако d _x² — орбиталь имеет другую форму. У неё по-прежнему две узловые поверхности, но они имеют коническую форму. Все эти волны амплитуды вероятности плавно спадают к нулю с удалением от ядра (протона), а не обрываются резко, как на этих диаграммах

При n=4 в дополнение к s, p, d-орбиталям число l может быть равно 3, что позволяет числу m принимать семь различных значений. Существует семь f-орбиталей. Эти f-орбитали имеют по три узловые поверхности и обладают очень сложными формами. Как объясняется в следующей главе, посвящённой атомам тяжелее водорода, лишь очень тяжёлые элементы обладают электронами на f-орбиталях, и эти электроны обычно не принимают участия в образовании химических связей. Многие молекулы, в особенности те, в которых основным элементом является углерод, так называемые органические молекулы, зависят в основном от 2s- и 2p-орбиталей. Однако молекулы, содержащие тяжёлые элементы, например металлы, могут зависеть также и от d-орбиталей.

В главе 11 мы построим обсуждение так, чтобы, отталкиваясь от свойств атома водорода, понять свойства всех атомов. Поскольку эти более крупные атомы содержат больше одного электрона, в игру вступает четвёртое квантовое число s. Опираясь на ряд простых правил, мы сможем понять многие свойства атомов и разобраться в том, как они образуют молекулы.

11. Многоэлектронные атомы и Периодическая таблица элементов

Свойства атомарной и молекулярной материи определяются квантовомеханическими особенностями атомов, из которых состоит вещество. Обычная поваренная соль — это хлорид натрия, NaCl. Na — это символ атома натрия. Его атомный номер — 11. Атомный номер — это число протонов в ядре, то есть величина положительного заряда ядра. У атома натрия 11 протонов в ядре и 11 отрицательно заряженных электронов. Хлор (обозначается Cl) имеет атомный номер 17. У атома хлора 17 протонов в ядре и 17 электронов. Когда поваренную соль, состоящую из маленьких белых кристаллов NaCl, опускают в воду, она растворяется. В воде Na становится положительно заряженным ионом натрия Na⁺ (это натрий, потерявший один электрон), хлор обращается в отрицательно заряженный хлорид-ион Cl⁻ (это хлор, присоединивший дополнительный электрон). Натрий отдаёт электроны хлору, и в результате получается катион натрия (положительно заряженный ион) и анион хлора (отрицательно заряженный ион). Заряды, которые несут катион натрия и анион хлора, делают эти ионы легко растворимыми в воде.

Метан — это природный газ, горящий в наших печах, в газовых сушилках для одежды и на тепловых электростанциях. Его химическая формула CH₄. Это означает, что он состоит из одного атома углерода (символ C, атомный номер 6), связанного с четырьмя атомами водорода (символ H, атомный номер 1). Метан не превращается в ионы, попадая в воду. В действительности он не растворяется в воде. Если не разогреть его до очень высокой температуры, как в пламени, он вообще не распадается на части. Почему NaCl распадается на отдельные ионы Na⁺ и Cl⁻ при растворении в воде, почему углерод всегда образует четыре химические связи и почему метан не распадается на части в воде, образуя ионы? Ответы на эти вопросы и объяснение множества свойств всех атомов можно получить, рассматривая природу многоэлектронных атомов и совокупность систематизированной информации об атомах, содержащейся в Периодической таблице элементов.

Водород — особый

Атом водорода отличается от всех прочих атомов, и это отличие чрезвычайно важно. Атом водорода состоит из положительно заряженного ядра (протона) и одного отрицательно заряженного электрона. Единственное электростатическое взаимодействие в нём — это притяжение электрона к протону, поскольку противоположно заряженные частицы притягиваются. Следующий по простоте атом — гелий. Гелий состоит из положительно заряженного ядра с зарядом +2 (символ He, атомный номер 2) и двух электронов, каждый с отрицательным зарядом −1. Каждый электрон притягивается к ядру; кроме того, два электрона отталкиваются друг от друга, поскольку оба заряжены отрицательно. Это взаимодействие называют электрон-электронным отталкиванием^{15}. Поскольку атом водорода имеет лишь один электрон, в нём нет электрон-электронного отталкивания.

На диаграмме энергетических уровней атома водорода (рис. 10.1) орбитали с одинаковым главным квантовым числом n имеют одну и ту же энергию. Таким образом, орбитали 2s и 2p обладают одинаковой энергией. У орбиталей 3s, 3p и 3d энергия тоже одинакова и т. д. Тот факт, что энергия зависит лишь от главного квантового числа, является следствием наличия у водорода единственного электрона. На рис. 10.2, 10.7 и 10.8 формы s-, p- и d-орбиталей существенно различаются. Однако в атоме водорода электрон в среднем находится на одинаковом расстоянии от ядра независимо от формы орбиталей. Поэтому он обладает одинаковой энергией вне зависимости от того, находится он на 3s-, 3p- или 3d-орбитали. Почему? Потому что электрон испытывает одинаковое притяжение к ядру, если усреднять его по пространственному распределению, задаваемому волновыми функциями 3s, 3p или 3d.

Формы орбиталей важны для атомов крупнее водорода

При наличии в атоме более чем одного электрона форма орбиталей становится важна. В атоме гелия, если два его электрона поместить на 2s-орбиталь, энергия будет ниже, чем если поместить их на 2p-орбиталь. В среднем два электрона на 2s-орбитали находятся дальше друг от друга, чем два электрона на 2p-орбитали. Электрон-электронное отталкивание увеличивает энергию. Поскольку два электрона на 2s-орбитали находятся дальше друг от друга, электрон-электронное отталкивание (повышающее энергию) будет не таким сильным, как если бы два электрона находились на 2p-орбитали. Поэтому в многоэлектронных атомах (во всех атомах, кроме водорода) 2s-орбиталь имеет более низкую энергию, чем 2p-орбиталь. При n=3 два электрона на 3s-орбитали в среднем находятся дальше друг от друга, чем если бы они занимали 3p-орбиталь, а два электрона на 3p-орбитали находятся дальше друг от друга, чем если бы они находились на 3d-орбитали. Поэтому 3s-орбиталь ниже по энергии, чем 3p-орбитали, которые, в свою очередь, ниже по энергии, чем 3d-орбитали. Однако 3s-орбитали выше по энергии, чем 2s-орбитали. В среднем электроны на 3s-орбитали находятся дальше от ядра, поскольку 3s-орбиталь больше, чем 2s-орбиталь (см. рис. 10.2, 10.5 и 10.6), а значит, слабее притягиваются к ядру. Следствием более слабого притяжения является более высокая энергия. Притяжение к ядру связывает электрон с ядром. Принятое в физике соглашение о знаке потенциальной энергии устанавливает, что более сильная связь соответствует более низкой энергии. Электроны проваливаются в притягивающий колодец положительно заряженного ядра. Чем сильнее притяжение, тем глубже погружается электрон в потенциальную яму и тем больше нужно энергии, чтобы извлечь из неё электрон, то есть оторвать его от ядра.

Энергетические уровни многоэлектронного атома

Для заданного главного квантового числа n энергия упорядочена следующим образом: ns<np<nd<nf. Для одного и того же типа орбитали чем больше n, тем выше энергия. Важная особенность многоэлектронных атомов состоит в том, что энергия зависит от двух квантовых чисел: n и l. Квантовое число l называют орбитальным, поскольку оно определяет форму орбитали.

На рис. 11.1 приведена диаграмма энергетических уровней для многоэлектронных атомов. При n=1 существует единственный тип орбитали: l=0 — это s-орбиталь, так что 1s-орбиталь имеет самый низкий уровень энергии. Для n=2 значение l может быть равно 0 или 1. Эти значения l порождают 2s-орбиталь и три различные 2p-орбитали. При l=1 существуют три возможных значения m:m = 1, 0, −1. Тут всё так же, как и у водорода. Важное отличие состоит в том, что у многоэлектронных атомов 2s-орбиталь имеет более низкую энергию, чем 2p-орбитали (см. рис. 11.1). При n=3 существуют 3s-орбиталь, 3p-орбитали и 3d-орбитали. Как видно из рис. 11.1, 3s-орбитали лежат ниже (по энергии), чем 3p-орбитали, которые, в свою очередь, лежат ниже 3d-орбиталей.

Очень важная особенность этого упорядочения энергетических уровней состоит в том, что энергетические уровни с разными значениями квантового числа n перемежаются. Хотя 3d-орбитали лежат выше 3p-орбиталей, энергия 4s-орбитали всё же ниже, чем 3d-орбитали (см. рис. 11.1). Порядок орбиталей также показан на рис. 11.1, где видно, что энергетические уровни следуют в порядке: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d и т. д. Как объясняется далее, перестановка уровней 4s и 3d приводит к появлению первого ряда переходных металлов, а перестановка 5s и 4d порождает второй ряд переходных металлов^{16}. Этот порядок очень важен при определении свойств различных атомов. Перестановки в этом порядке и смысл рядов переходных металлов прояснятся после обсуждения Периодической таблицы элементов. Однако сначала надо разобраться, как электроны заполняют энергетические уровни, изображённые на рис. 11.1.

Рис. 11.1.Диаграмма энергетических уровней для атомов с множеством электронов. Для интервалов между уровнями масштаб не соблюдается. Энергия зависит от главного квантового числа n и орбитального квантового числа l, и в этом заключается отличие от атома водорода (см. рис. 10.1), где энергия зависит только от n. Для n=4 существует одна s-орбиталь (l=0), три различные p-орбитали (l=1), пять различных d-орбиталей (l=2) и семь различных f-орбиталей (l=3)

Три правила заполнения энергетических уровней электронами

Атом водорода имеет ядро с зарядом +1 и единственный отрицательно заряженный электрон. Атом гелия имеет ядро с зарядом +2 и два отрицательно заряженных электрона. Далее идёт литий (Li) с зарядом ядра +3 (атомный номер 3) и тремя отрицательными электронами, за которым следует бериллий (Be) с ядром +4 и четырьмя отрицательными электронами и т. д. Вопрос состоит в следующем: если есть атом с определённым числом электронов вроде бериллия, у которого их четыре, то на каких энергетических уровнях будут располагаться эти электроны? У водорода самое низкое энергетическое состояние — то, в котором единственный электрон находится на 1s-орбитали. Если возбудить 1s-электрон водорода до, скажем, состояния 2p (добавив ему энергии за счёт поглощения света или с помощью электрической дуги), он свалится обратно в низшее энергетическое состояние и, согласно закону сохранения энергии, испустит фотон. Такая эмиссия фотонов с различных энергетических уровней атома водорода порождает линейчатый спектр, обсуждавшийся в главах 9 и 10. Однако неясно, что делать, когда электронов больше одного. Должны ли все четыре электрона бериллия переходить на 1s-орбиталь? Оказывается, это невозможно.

Квантовая теория, подтверждённая бесчисленными экспериментами, дала три правила, которые определяют, как размещать электроны по энергетическим уровням (см. рис. 11.1) для получения электронных конфигураций различных атомов. Мы будем опираться на так называемый ауфбау-принцип^{17}, три правила которого указывают, как размещать электроны по энергетическим уровням в правильном порядке — как в настоящих атомах. Мы будем строить атомы и конструировать Периодическую таблицу, «заселяя» всё больше электронов во всё более крупные атомы на соответствующие энергетические уровни. Многие свойства атомов, их склонность приобретать или терять электроны, образуя ионы, число химических связей, которые они образуют, становятся понятны благодаря ауфбау-принципу, позволяющему построить Периодическую таблицу.

Правило 1: принцип запрета Паули

Правило 1 — это принцип запрета Паули. Он утверждает, что ни у каких двух электронов в атоме (или молекуле) не могут совпадать все четыре квантовых числа. Существуют четыре квантовых числа: n, l, m и s. Для водорода мы использовали первые три, но теперь становится важным и s. Число s может принимать лишь два значения: s = +½ или −½. Поэтому на конкретной орбитали, заданной квантовыми числами n, l, m, может располагаться не более двух электронов. Один из этих электронов будет иметь s=+½, а другой — s=−½. Например, 1s-орбиталь имеет n=1, l=0, m=0 и s = +½ или −½. Таким образом, 1s-орбиталь могут занимать два электрона: один со спином +½ и один со спином −½.

Для 2p-орбиталей n=2, l=1, m=1, 0, −1 и s = +½ или −½. Орбитали p_x, p_y и p_z (см. рис. 10.7) могут содержать по два электрона каждая: один с s=+½, а другой обязательно с s=−½. Таким образом, всего может быть шесть 2p-электронов — по два на каждой из трёх орбиталей. 3d-орбитали имеют квантовые числа n=3, l=2, m = 2, 1, 0, −1, −2 и s = +½ или −½. Существует пять 3d-орбиталей, и на каждой могут размещаться два электрона (s = +½ или −½) — всего 10 d-электронов по два на пяти орбиталях. Наконец, существует семь 4f-орбиталей с квантовыми числами n=4, l=3, m = 3, 2, 1, 0, −1, −2, −3 и s = +½ или −½. Следовательно, всего может быть 14 f-электронов, по два на каждой из семи орбиталей.

Когда два электрона находятся на одной орбитали, их спины называют спаренными. Электрон на орбитали (энергетическом уровне) изображается стрелкой (см. рис. 11.2). Спиновое квантовое число s=+½ изображается стрелкой, направленной вверх. Спиновое квантовое число s=−½ изображается стрелкой, направленной вниз. На любой отдельно взятой орбитали может быть не более одной стрелки вверх и одной стрелки вниз.

Рис. 11.2.Слева: электрон изображён стрелкой на орбитали. Справа: два электрона на одной орбитали. Чтобы удовлетворять принципу запрета Паули, их квантовые числа s должны иметь значения +½ и −½, представленные стрелками, направленными вверх и вниз. О таких спинах говорят, что они спаренные

Правило 2: сначала наименьшая энергия, но без нарушения принципа Паули

Правило 2 состоит в том, что орбитали заполняются электронами в порядке увеличения энергии. Электроны сначала заселяют самый нижний доступный энергетический уровень, но при этом не должен нарушаться принцип Паули. Таким образом, в атоме гелия (He) электроны могут занять энергетический уровень 1s — один со спином «вверх» (s=+½) и один со спином «вниз» (s=−½). Три квантовых числа совпадают, но значения s различаются, так что принцип Паули не нарушается. Li — следующий по величине атом, с тремя электронами. Третий электрон не может разместиться на уровне 1s, поскольку все четыре его квантовых числа (n, l, m и s) совпадали бы с одним из двух других электронов, и, значит, третий электрон должен занять более высокий уровень — 2s-орбиталь. Это самый низкий из доступных уровней для третьего электрона. Поэтому правило 2 предписывает ему заселиться именно сюда.

Правило 3 (правило Хунда): спины не спариваются, если это возможно без нарушения правил 1 и 2

Правило 3 называется правилом Хунда. Оно утверждает, что, заполняя орбитали с одинаковой энергией, электроны остаются по возможности неспаренными. На рис. 11.3 правило Хунда проиллюстрировано на примере 2p-орбиталей. Первый электрон, обозначенный на рисунке цифрой 1, занимает 2p_x-орбиталь. Этот выбор произволен, поскольку все три 2p-орбитали имеют одинаковую энергию. Согласно правилу Хунда, второй электрон займёт одну из двух других 2p-орбиталей, имеющих одинаковую энергию, так чтобы спины не спаривались. В нашем примере он попадает на 2p_y-орбиталь. Третий электрон должен заселиться на 2p_z-орбиталь — это единственный способ соблюсти правило Хунда, а также правила 1 и 2. Наконец, четвёртый электрон спаривается с одним из остальных электронов. Как показано на рисунке, он занимает 2p_x-орбиталь. Его спин должен быть направлен вниз, чтобы соблюдался принцип Паули, правило 1.

Рис. 11.3. Иллюстрация правила Хунда. При заселении 2p-орбиталей электрон 1 занимает 2p _x -орбиталь, электрон 2 — 2p _y , электрон 3 — 2p _z . Все они имеют спин, направленный вверх. Электрон 4 обязан будет иметь спин, направленный вниз, чтобы спариться во избежание нарушения принципа Паули

Правило Хунда возникает потому, что оно даёт электронные конфигурации с наименьшей возможной энергией. При заселении двух электронов на две разные 2p-орбитали они размещаются в среднем дальше друг от друга, чем при заселении на одну и ту же орбиталь. Энергия уменьшается, поскольку удаление электронов друг от друга приводит к ослаблению их взаимного отталкивания. Таким образом, правило Хунда, по сути, требует помещать электроны по возможности на разные орбитали. Хотя факт уменьшения энергии при сохранении электронов неспаренными весьма важен, величина, на которую снижается энергия, незначительна. Поэтому лучше спарить электрон 4 на 2p_x-орбитали, чем разместить его неспаренным на более высокоэнергетической 3s-орбитали.

Периодическая таблица элементов

Итак, мы изложили правила расселения электронов по энергетическим уровням, изображённым на рис. 11.1. Теперь эти правила будут использоваться для понимания многочисленных свойств атомов и Периодической таблицы элементов. Кроме того, точно такие же правила будут очень важны при обсуждении молекул в последующих главах. Однако сначала нам необходимо познакомиться с Периодической таблицей (рис. 11.4).

В Периодической таблице каждому элементу соответствует клетка. В этой клетке записан символ элемента, а также его атомный номер. Атомный номер — это число положительно заряженных протонов в ядре элемента. Для нейтрального атома (в отличие от положительно или отрицательно заряженного иона) атомный номер — это также число отрицательно заряженных электронов. О строении Периодической таблицы будет во всех подробностях рассказано далее. В её левом верхнем углу расположен водород (символ H, атомный номер 1). В правом верхнем углу находится гелий (символ He, атомный номер 2). Под водородом располагается литий (символ Li, атомный номер 3).

Рис. 11.4. Периодическая таблица элементов

Многие символы являются просто аббревиатурами названий. Но это не всегда так. Например, свинцу (элемент 82) соответствует буквенный символ Pb, производный от латинского названия свинца plumbum. Поскольку по символам не всегда легко понять, как называется элемент, в табл. 11.1 приведены названия, символы и атомные номера элементов. Названия элементов в таблице упорядочены по алфавиту. Если по буквенному символу элемента вы не можете определить его название, просматривайте сверху вниз колонку символов, пока не найдёте нужный.

Таблица 11.1. Список элементов (в алфавитном порядке названий)

Элемент, Символ, Атомный №

Азот N 7

Актиний Ac 89

Алюминий Al 13

Америций Am 95

Аргон Ar 18

Астат At 85

Барий Ba 56

Бериллий Be 4

Берклий Bk 97

Бор B 5

Борий Bh 107

Бром Br 35

Ванадий V 23

Висмут Bi 83

Водород H 1

Вольфрам W 74

Гадолиний Gd 64

Галлий Ga 31

Гафний Hf 72

Гелий He 2

Германий Ge 32

Гольмий Ho 67

Дармштадтий Ds 110

Диспрозий Dy 66

Дубний Db 105

Европий Eu 63

Железо Fe 26

Золото Au 79

Индий In 49

Иод I 53

Иридий Ir 77

Иттербий Yb 70

Иттрий Y 39

Кадмий Cd 48

Калий K 19

Калифорний Cf 98

Кальций Ca 20

Кислород O 8

Кобальт Co 27

Коперниций Cn 112

Кремний Si 14

Криптон Kr 36

Ксенон Xe 54

Кюрий Cm 96

Лантан La 57

Ливерморий Lv 116

Литий Li 3

Лоуренсий Lr 103

Лютеций Lu 71

Магний Mg 12

Марганец Mn 25

Медь Cu 29

Мейтнерий Mt 109

Менделевий Md 101

Молибден Mo 42

Мышьяк As 33

Натрий Na 11

Неодим Nd 60

Неон Ne 10

Нептуний Np 93

Никель Ni 28

Ниобий Nb 41

Нобелий № 102

Олово Sn 50

Осмий Os 76

Палладий Pd 46

Платина Pt 78

Плутоний Pu 94

Полоний Po 84

Празеодим Pr 59

Прометий Pm 61

Протактиний Pa 91

Радий Ra 88

Радон Rn 86

Резерфордий Rf 104

Рений Re 75

Рентгений Rg 111

Родий Rh 45

Ртуть Hg 80

Рубидий Rb 37

Рутений Ru 44

Самарий Sm 62

Свинец Pb 82

Селен Se 34

Сера S 16

Серебро Ag 47

Сиборгий Sg 106

Скандий Sc 21

Стронций Sr 38

Сурьма Sb 51

Таллий Tl 81

Тантал Ta 73

Теллур Te 52

Тербий Tb 65

Технеций Tc 43

Титан Ti 22

Торий Th 90

Тулий Tm 69

Углерод C 6

[Унунпентий] Uup 115

[Унунтрий] Uut 113

Уран U 92

Фермий Fm 100

Флеровий Fl 114

Фосфор P 15

Франций Fr 87

Фтор F 9

Хассий Hs 108

Хлор Cl 17

Хром Cr 24

Цезий Cs 55

Церий Ce 58

Цинк Zn 30

Цирконий Zr 40

Эйнштейний Es 99

Эрбий Er 68

В Периодической таблице (см. рис. 11.4) отмечены металлы (белый тон), полуметаллы (полупроводники, тёмно-серый тон) и неметаллы (светло-серый тон). Полуметаллы — эта полоса между металлами (к которым относится большинство элементов) и неметаллами, которые располагаются в верхней правойчасти таблицы. В нижней части таблицы находятся два ряда элементов, называемых лантаноидами и актиноидами. Лантаноиды начинается с элемента лантана (La), а актиноиды — с актиния (Ac). Они заполняют пробел, отмеченный в таблице. Эти два ряда атомов, в которых задействованы f-орбитали, помещают под остальной таблицей, чтобы она не становилась слишком широкой.

Прежде чем перейти к рассмотрению свойств элементов, мы вкратце пройдёмся по первым двум строкам Периодической таблицы, чтобы почувствовать её структуру и понять, что такое «заполненная оболочка» в применении к электронной конфигурации. Затем мы обсудим, как использовать таблицу для понимания свойств элементов.

Структура Периодической таблицы

С учётом диаграммы энергетических уровней (см. рис. 11.1) и трёх правил заселения энергетических уровней электронами водород (символ H, атомный номер 1) имеет один электрон на 1s-орбитали согласно правилу о том, что самые нижние уровни заселяются первыми, если это не нарушает принцип Паули. Водород находится в верхнем левом углу Периодической таблицы. Это первый элемент в строке 1. Следующий элемент — это гелий (He, 2). На его 1s-орбитали находятся два электрона с противоположными спинами (стрелка вверх и стрелка вниз, как показано на рис. 11.2). Эта конфигурация удовлетворяет принципу Паули и правилу о том, что позиции с наименьшей энергией занимаются первыми, который перекрывает правило Хунда, поскольку потребовалось бы слишком много энергии, чтобы поместить второй электрон гелия на энергетический уровень 2s (см. рис. 11.1). Гелий находится в верхнем правом углу Периодической таблицы — он завершает первую строку. Эта первая строка состоит из двух элементов — H и He с электронами на уровне n=1. Строки таблицы также называют периодами. Гелий завершает первый период. Говорят, что гелий имеет заполненную (или замкнутую) электронную оболочку, поскольку это старший элемент, все электроны которого имеют n=1.

Следующий элемент — это литий (Li, 3). Он имеет три электрона. Первые два электрона занимают энергетический уровень 1s, подчиняясь правилу о том, что сначала заселяется самый нижний доступный уровень. Третий электрон не может разместиться на 1s-орбитали, поскольку это нарушало бы принцип Паули. Поэтому третий электрон занимает 2s-орбиталь. В Периодической таблице Li располагается под H. H — это первый элемент с электроном, находящимся в оболочке n=1. Li — это первый элемент второго периода, соответствующего оболочке с n=2.

Следующий элемент — это бериллий (Be, 4). Четвёртый электрон также занимает 2s-орбиталь. Это самое низкое энергетическое состояние, не нарушающее принцип Паули. Далее следует бор (B, 5) с пятью электронами. Пятый электрон не может занять 2s-орбиталь, поскольку это нарушило бы принцип Паули, утверждающий, что на одной орбитали может находиться не более двух электронов, которые должны иметь противоположные спины (спиновое квантовое число s=+½ или s=−½). Поэтому пятый электрон заселяется на 2p-орбиталь, а на какую именно из 2p-орбиталей, не имеет значения. Следуя рис. 11.3, будем считать, что это 2p_x-орбиталь. Между Be и B в таблице есть разрыв. Причина его появления прояснится далее, когда мы будем обсуждать четвёртый период.

Следующим идёт углерод (C, 6) с шестью электронами. Теперь в игру вступает правило Хунда, и мы помещаем шестой электрон на 2p_y-орбиталь, следуя схеме, представленной на рис. 11.3. Следующий элемент — азот (N, 7). Согласно правилу Хунда, седьмой электрон N заселяется на 2p_z-орбиталь, чтобы ни один из электронов на p-орбиталях не был спаренным. Кислород (O, 8) имеет восемь электронов. Восьмой электрон должен быть спаренным, поскольку из первых семи электронов два занимают 1s-орбиталь, ещё два — 2s и по одному электрону находится на каждой из 2p-орбиталей. Чтобы избежать спаривания спинов, надо поместить восьмой электрон на 3s-орбиталь, которая требует значительно более высокой энергии. Поэтому, как и на рис. 11.3, восьмой электрон заселяется на 2p_x-орбиталь. Фтор (F, 9) обладает девятым электроном, который располагается на 2p_y-орбитали. Наконец, неон (Ne, 10) завершает период n=2 с оболочкой из 10 электронов. Десятый электрон заселяется на 2p_z-орбиталь.

Конфигурации с замкнутыми оболочками

Электронная конфигурация неона изображена на рис. 11.5. Ни один дополнительный электрон не может заселиться на вторую оболочку (орбитали с n=2) без нарушения принципа Паули. Как будет объяснено далее, элементы He, Ne, Ar, Kr и т. п., занимающие последнюю колонку в правой части Периодической таблицы, — особые. Эти элементы называются благородными газами. Все они обладают замкнутыми (заполненными) оболочками, то есть со следующего элемента, имеющего на один электрон больше, начинают заполняться орбитали с квантовым числом n на единицу больше, а значит, обладающие значительно более высокой энергией.

Рис. 11.5. Электронная конфигурация атома неона (Ne, 10). Вторая оболочка заполнена

Атомы стремятся образовывать конфигурации с замкнутыми оболочками

Теперь мы готовы использовать диаграмму энергетических уровней (см. рис. 11.1) и наши три правила расселения электронов по энергетическим уровням для объяснения строения Периодической таблицы и свойств элементов. В следующих главах будет подробно разбираться вопрос о том, что удерживает атомы вместе в составе молекул, однако очень многое можно понять на основе поразительно простого правила: атомы будут захватывать или отдавать электроны, стремясь к ближайшей конфигурации с заполненной оболочкой. Замкнутые электронные оболочки — это электронные конфигурации благородных газов, которые располагаются в правой колонке Периодической таблицы. Конфигурации с замкнутыми оболочками исключительно стабильны. Благородные газы, также называемые инертными, обладают заполненными оболочками и в основном химически инертны. Благородные газы с малыми атомными номерами — гелий, неон и аргон — вообще не образуют химических соединений. Благородные газы с более высокими атомными номерами в особых условиях можно заставить образовать небольшое число соединений. Атомы, отличные от благородных газов, меняются в направлении, приближающем их к образованию устойчивой замкнутой электронной оболочки.

Есть два способа, которыми атом может изменить число своих электронов, чтобы достичь замкнутости электронной оболочки. Первый способ — стать положительным ионом (катионом) или отрицательным ионом (анионом). Атом отдаёт один или больше своих электронов и становится положительно заряженным (катионом) или захватывает дополнительные электроны и становится отрицательно заряженным (анионом). Альтернативный путь для атома состоит в том, чтобы совместно использовать электроны с одним или несколькими другими атомами. Когда два или более атома объединяют электроны, это действует так, как если бы каждый атом обладал необходимыми ему электронами. Тем самым атом с меньшим числом электронов, чем требуется для образования следующий замкнутой электронной оболочки, получает нужное их число, но то же самое происходит и с другими атомами, задействованными в совместном использовании.

Когда атомы совместно используют электроны, чтобы получить такое их число, которое требуется для образования следующей замкнутой оболочки, это совместное использование удерживает атомы вместе. Совместное использование электронов приводит к тому, что энергия соединённых атомов становится ниже энергии отдельных недозаполненных оболочек. Это уменьшение энергии связывает атомы друг с другом. Такой тип химической связи называется ковалентной связью. Ковалентные связи представляют собой основной тип связи в химии. Природа ковалентной связи подробно разбирается в главе 12 на примере простейшей молекулы — водорода, а более сложные молекулы обсуждаются в последующих главах.

Свойства атомов

Переходя к обсуждению свойств атомов, основанному на Периодической таблице, начнём с водорода. Водород — это особый атом, поскольку у него лишь один электрон, и это первый элемент в Периодической таблице. В первой строке Периодической таблицы гелий имеет заполненную оболочку с двумя электронами на 1s-орбитали. Водород может обзавестись замкнутой конфигурацией оболочки, как у гелия, позаимствовав электрон у другого атома в порядке совместного использования. Например, один атом водорода может совместно использовать электрон с другим атомом водорода, образовав молекулу водорода. Обозначение молекулы водорода H₂. Индекс указывает, сколько атомов данного типа содержится в молекуле. Благодаря совместному использованию электронов каждый из атомов водорода ощущает себя так, как если бы у него было два электрона, то есть замкнутая электронная оболочка, подобная той, что имеется у гелия.

Как мы увидим далее, водород может образовывать другие молекулы, но поскольку ему требуется лишь один электрон, чтобы получить заполненную электронную оболочку, как у гелия, он может образовывать одну химическую связь. Гелий имеет замкнутую оболочку. Он не способен образовывать какие-либо химические связи. Не существует молекул, в которые входил бы атом гелия. Почему именно так происходит, описывается в главе 12. Гелий замыкает первый период.

Следующий элемент — это литий (Li), который располагается в Периодической таблице непосредственно под H. Li может получить заполненную конфигурацию оболочки, как у гелия, отдав электрон. Поэтому Li образует положительные ионы Li¹⁺. В твёрдом виде Li является металлом. Металлы способны проводить электричество, а значит, электроны могут свободно перемещаться от одного атома к другому. Природа металлов и электропроводности будет обсуждаться в главе 19. Металлы отличаются тем свойством, что, будучи одиночными атомами, они легко могут отдать один или несколько электронов. Электрон, отданный литием, должен куда-то деться. Он перейдёт к другому атому, которому нужно получить электрон, чтобы образовать отрицательный ион. Таким образом, для образования иона Li¹⁺ литию нужен партнёр (см. обсуждение ниже, где мы добираемся до другой стороны Периодической таблицы).

Следующий элемент — это бериллий. Бериллий будет отдавать два электрона, чтобы вернуться к конфигурации гелия с замкнутой электронной оболочкой. Поэтому бериллий будет образовывать ионы с зарядом +2 (Be²⁺). Поскольку бериллий легко отдаёт электроны, твёрдый бериллий является металлом. Следующий элемент — это бор. Он может отдать электроны, чтобы вернуться к конфигурации гелия с замкнутой оболочкой. Поэтому он образует ионы с зарядом +3 и является металлом.

Дальше всё изменяется. Следующий элемент — это углерод. Ему понадобилось бы отдать четыре электрона, чтобы вернуться к конфигурации гелия, но он также мог бы присоединить четыре электрона, чтобы перейти к следующей замкнутой конфигурации оболочки, такой как у неона. Как показано на рис. 11.5, атом Ne обладает второй по счёту замкнутой электронной оболочкой. У него два электрона находятся на 1s-орбитали, а затем оболочка с n=2 заполнена двумя электронами на 2s-орбиталях и шестью электронами на трёх 2p-орбиталях. Вместо того чтобы отдавать так много электронов, возвращаясь к конфигурации гелия, атом C может двинуться вперёд — к конфигурации неона, присоединив четыре электрона путём создания четырёх ковалентных связей.

Например, метан (природный газ) имеет молекулу CH₄, в которой каждый атом H связан с центральным атомом C. Углерод совместно использует четыре электрона, по одному от каждого атома водорода, и тем самым получает замкнутую электронную конфигурацию неона. Каждый атом H использует один электрон совместно с атомом C, получая тем самым дополнительный электрон для формирования замкнутой конфигурации электронной оболочки, как у гелия. Это очень важно. За счёт ковалентных связей (совместного использования электронов) каждый атом получает замкнутую конфигурацию оболочки. Другой чрезвычайно важный факт состоит в том, что атом С всегда создаёт четыре связи, поскольку нуждается в совместном использовании четырёх электронов для достижения конфигурации неона. Этот факт играет фундаментальную роль для органической химии и биохимии, что подробно обсуждается в последующих главах.

Следующий элемент — азот. Атом N нуждается в трёх электронах, чтобы достичь конфигурации неона, поэтому он образует три ковалентные связи. Например, он может соединяться с атомами H, образуя молекулу NH₃ — аммиак. Кислороду нужно два электрона, чтобы получить замкнутую конфигурацию оболочки неона, так что он образует две связи и, например, участвует в образовании молекулы воды (H₂O). Таким образом, из этих простых соображений уже становится понятна последовательность соединений: CH₄, NH₃ и H₂O. Связи, образуемые с участием атомов C, N и O, будут обсуждаться в следующих главах, где идёт речь о молекулах, содержащих эти атомы, но они всегда образуют 4, 3 и 2 связи соответственно.

Следующий элемент — это фтор. Атом фтора лишь на один электрон отстаёт от замкнутой оболочки атома Ne. Он имеет столь сильное сродство к электрону, что склонен образовывать отрицательный ион F¹⁻, захватывая «лишний» электрон. Этот электрон должен откуда-то появиться, и атом F образует соединения, которые в общем случае называются солями. Например, соединение LiF имеет вид белых кристаллов. В этих кристаллах Li, которому нужно отдать электрон, чтобы достичь конфигурации гелия, передаёт электрон атому F. В результате кристалл LiF состоит из ионов Li¹⁺ и ионов F¹⁻. Ионы Li¹⁺ обладают замкнутой оболочкой, как у атома He, а ионы F¹⁻ имеют замкнутую оболочку, как у атома Ne.

Кристаллы LiF, как и все соли, легко растворяются в воде. Такой кристалл скрепляется посредством электростатических взаимодействий. Положительные и отрицательные ионы притягиваются друг к другу. Они располагаются в кристалле таким образом, что притяжение между катионами и анионами превосходит отталкивание между одними катионами и другими катионами, а также между одними анионами и другими анионами. Вода может окружать как положительные, так и отрицательные ионы, причём это делает общую энергию системы (воды, окружающей катионы и анионы) ниже, чем у кристалла LiF, погружённого в воду. Это называется сольватацией. Вода сольватирует ионы, и поэтому ионные кристаллы, такие как LiF, растворяются в воде. Сольватация обсуждается в главе 15.

Атом F будет образовывать соли с атомами из левой части таблицы, которым нужно отдавать электроны, чтобы достичь замкнутой конфигурации оболочки. В молекуле LiF фтор получает электрон, а литий его отдаёт. F также может получить заполненную оболочку, такую как у неона, создав другого рода ковалентные связи. Как описывается ниже, он может соединиться с серой (S), образовав SF₂.

За фтором в Периодической таблице следует неон. Он имеет заполненную оболочку (см. рис. 11.5). Атом Ne не стремится ни присоединять, ни отдавать электроны. Он не образует химических соединений. Ne завершает вторую строку Периодической таблицы.

За неоном идёт натрий. У него на один (3s) электрон больше, чем в конфигурации Ne. Как и Li, находящийся прямо над ним, Na будет легко отдавать электроны, образуя катион Na¹⁺. Сделав это, он получает такую же электронную конфигурацию, как у Ne. Твёрдый натрий является металлом, который проводит электричество (электроны), поскольку его 3s-электрон слабо с ним связан. Подобно LiF, соединение NaF — это соль, которая хорошо растворима в воде.

Следующим идёт магний. Mg будет отдавать два электрона для достижения неоновой замкнутой конфигурации оболочки, образуя ионы Mg²⁺. Это металл, который проводит электричество, поскольку он легко отдаёт два своих 3s-электрона. Он будет образовывать соли, например MgF₂. Это означает, что в кристалле содержится два аниона фтора на каждый катион магния с зарядом +2. MgF₂ хорошо растворяется в воде.

За магнием следует алюминий. Твёрдый алюминий является металлом. Алюминий образует катионы Al³⁺.

Как и в случае с углеродом во второй строке, на кремнии всё меняется. Si будет создавать четыре ковалентные связи, чтобы совместно использовать (фактически присоединять) четыре электрона, получив тем самым замкнутую конфигурацию электронной оболочки аргона (см. Периодическую таблицу). Например, кремний образует соединение SiH₄. Фосфор для достижения такой конфигурации, как у аргона, будет создавать три ковалентные связи, например PH₃, а сере потребуются две ковалентные связи для получения заполненной оболочки аргона. Она образует сероводород H₂S — ядовитый газ, обладающий очень резким запахом тухлых яиц. Как уже отмечалось, сера может также создавать ковалентные связи, образуя соединение SF₂.

За серой следует хлор. Подобно фтору, который нуждается лишь в одном электроне, чтобы сформировать замкнутую конфигурацию оболочки неона, атому Cl требуется лишь один электрон, чтобы получить замкнутую конфигурацию электронной оболочки аргона, так что он склонен образовывать ион Cl¹⁻, присоединяя лишний электрон. В Периодической таблице элементы в столбце рядом с благородными газами, то есть во второй колонке справа, образуют анионы с зарядом −1. Эти элементы (F, Cl, Br, I, At) называются галогенами. Хлор даёт нам обычную поваренную соль — хлорид натрия NaCl — кристаллы, состоящие из ионов Na¹⁺ и Cl¹⁻. Как и LiF, NaCl может растворяться в воде, поскольку катионы и анионы сольватируются молекулами H₂O. Это существенно отличается от поведения метана CH₄, который не растворяется в воде. Углерод и атомы водорода достигают замкнутости своих оболочек за счёт совместного использования электронов посредством образования ковалентных связей. Если молекулу метана разделить на части, оболочки атомов перестанут быть замкнутыми. В этом отличие от кристалла NaCl, который может распадаться на Na¹⁺ и Cl¹⁻, причём катион и анион имеют заполненные оболочки. Молекулы, содержащие только углерод и водород, из которых состоят нефть, бензин и метан, называются углеводородами. Они нерастворимы в воде. Углеводороды обсуждаются в главах 14, 15 и 16.

За Cl следует аргон (Ar), который имеет замкнутую электронную оболочку (рис. 11.6). У него 18 электронов, два из них — 1s, два — 2s, шесть находится на трёх 2p-орбиталях, два — на 3s-орбиталях и шесть — на трёх 3p-орбиталях. Аргон — инертный газ. Он не образует химических соединений^{18}.

Рис. 11.6. Электронная конфигурация аргона (Ar, 18). Третья оболочка заполнена

При движении сверху вниз по столбцам атомы становятся крупнее

Чем ниже мы спускаемся по столбцам Периодической таблицы, тем больше становятся размеры атомов. Так, атом Li крупнее атома H, атом Na больше атома Li и т. д. Это объясняется двумя обстоятельствами. Во-первых, дополнительные электроны занимают орбитали с бо́льшим главным квантовым числом n. Атом H имеет 1s-электрон, атом Li — 2s-электрон, атом Na — 3s-электрон. Глядя на рис. 10.2-10.6, которые относятся к атому водорода, можно заметить, что волновая функция 3s намного больше, чем 2s, которая, в свою очередь, намного больше, чем 1s. Однако по мере движения вниз по столбцам возрастает также и положительный заряд ядра. Заряд ядра — это то же самое, что и атомный номер, который есть у всех атомов в Периодической таблице и приведён в списке элементов. С увеличением положительного заряда ядра отрицательно заряженные электроны притягиваются всё ближе к нему. Однако этого недостаточно, чтобы скомпенсировать тот факт, что по мере спуска по столбцам таблицы электроны занимают орбитали со всё большим главным квантовым числом (n). Увеличение размеров с ростом n оказывается значимее эффекта усиливающегося притяжения электронов к ядру, так что размеры атомов при спуске вниз по столбцам возрастают.

При движении слева направо по строкам атомы становятся меньше

Если смещаться по строке слева направо, атомы будут становиться всё меньше. Так, атом Be меньше атома Li, атом B меньше атома Be, атом C меньше атома B и т. д. Уменьшение размеров происходит потому, что все атомы имеют одно и то же главное квантовое число n, однако заряд ядра возрастает. И вновь два эффекта конкурируют друг с другом. Положительный заряд ядра возрастает при смещении вправо по строке. Возрастающий положительный заряд будет притягивать электроны всё ближе к ядру. Однако вместе с тем электронов становится больше. Отрицательно заряженные электроны отталкивают друг друга. Чтобы снизить эффект этого взаимного отталкивания электронов, электронное облако (волна амплитуды вероятности) становится больше. Положительный заряд в центре притягивает к себе все электроны. Однако отрицательно заряженное электронное облако распределено вокруг ядра. С чисто классических позиций в каждый момент электроны, находящиеся с одной стороны атома, отталкиваются электронами, находящимися с другой стороны атома, не так сильно, как они притягиваются ядром, расположенным в центре. Поэтому притяжение побеждает, и атомы становятся меньше по мере движения по строке слева направо.

Первый ряд переходных металлов

Итак, мы добрались до четвёртой строки. За аргоном следует первый элемент четвёртой строки — калий (K). Атом K имеет один 4s-электрон сверх конфигурации аргона. Теперь уже ясно, что он будет образовывать ионы K¹⁺, чтобы вернуться к замкнутой конфигурации электронной оболочки аргона. В твёрдом виде калий является металлом и проводит электричество. Соль KCl является небольшой составляющей морской соли, которая в основном представлена солью NaCl. Соль KCl растворяется в воде, образуя ионы K¹⁺ и Cl¹⁻. За K следует кальций (Ca), который имеет два 4s-электрона сверх конфигурации аргона. Это металл, который образует ионы Ca²⁺, отдавая два своих 4s-электрона, чтобы получить замкнутую конфигурацию электронной оболочки аргона. Он образует такие соли, как CaCl₂, которая легко растворяется в воде, образуя катион кальция с зарядом +2 и два хлорид-иона.

И вот теперь у нас происходит большое изменение. На диаграмме энергетических уровней электронов атомов (см. рис. 11.1) видно, что 3d-орбитали расположены выше по энергии, чем 4s-орбитали, но ниже 4p-орбиталей. Как уже говорилось ранее в этой главе, промежуточное положение 3d-орбиталей между 4s- и 4p-орбиталями приводит к появлению первого ряда переходных металлов в Периодической таблице. Существует пять 3d-орбиталей. Принцип Паули гласит, что на каждой орбитали может быть не более двух электронов. Тогда на пяти 3d-орбиталях может находиться десять электронов, что приводит к появлению десяти переходных металлов — от скандия до цинка (см. Периодическую таблицу). Поэтому после Ca идут десять элементов, которые появляются за счёт заполнения 3d-орбиталей. Все они являются металлами, многие из которых широко известны: железо (Fe), медь (Cu), никель (Ni), цинк (Zn) и хром (Cr). Все они легко образуют ионы. Первые два элемента в строке, такие как K и Ca или Na и Mg, всегда образуют катионы с одним конкретным зарядом: +1 для первого столбца (Na¹⁺ и K¹⁺) и +2 — для второго (Mg²⁺ и Ca²⁺). Однако переходные металлы могут образовывать различные катионы. О них говорят, что они имеют состояния с разной степенью окисления. Когда металл отдаёт электрон, то говорят, что он окисляется. Состояние окисления определяется числом отданных электронов.

Рассмотрим железо. Оно может иметь степень окисления +2 и +3, то есть образует катионы Fe²⁺ и Fe³⁺. Образование Fe²⁺ легко понять. Fe может, подобно Ca, потерять два своих 4s-электрона, приобретя степень окисления +2. Кроме того, Fe имеет шесть 3d-электронов. В соответствии с правилом Хунда эти электроны будут оставаться по возможности неспаренными. Пять электронов могут по одному занять пять 3d-орбиталей. Это наполовину заполненная конфигурация является частично стабильной. Железо содержит ещё один 3d-электрон сверх этой конфигурации с наполовину заполненными 3d-орбиталями, так что атом Fe будет легко расставаться с этим 3d-электроном в дополнение к двум 4s-электронам, приобретая степень окисления +3. Поэтому Fe может образовывать такие соли, как FeCl₂ и FeCl₃.

Кроме того что 3d-электроны порождают первый ряд переходных металлов, они также ответственны за ещё одно важное молекулярное явление. Как уже говорилось, кислород будет образовывать две ковалентные связи (использовать совместно с другими атомами два электрона), чтобы достичь электронной конфигурации Ne. Пример тому — молекула воды H₂O. Сера, которая расположена прямо под кислородом, образует соединение H₂S, аналогичное H₂O. Однако она также может образовывать соединение SF₆, задействуя 3d-орбитали, которые близки по энергии к 3p-орбиталям. У кислорода нет подобных соединений, поскольку первый набор орбиталей (3d) расположен значительно выше по энергии, чем 2s- и 2p-орбитали, которые участвуют в образовании связей у элементов второй строки Периодической таблицы.

Первая серия переходных металлов завершается, когда заполнены все 3d-орбитали. Далее следует элемент галлий (Ga). Ga — это металл, и, подобно алюминию, он будет образовывать ионы с зарядом +3. Конфигурация, в которой 3d-орбитали целиком заполнены, является очень устойчивой, поэтому Ga образует только катионы с зарядом +3. Стабильность заполненных 3d-орбиталей также можно наблюдать на примере цинка. Zn образует только ионы с зарядом +2, отдавая два своих 4s-электрона. Вслед за Ga идут германий (Ge), мышьяк (As) и селен (Se), которые обычно образуют четыре, три и две ковалентные связи соответственно, чтобы получить замкнутую конфигурацию электронной оболочки, как у криптона (Kr). Дополнительные связи у Ge, As и Se, как и у элементов, расположенных непосредственно над ними, могут создаваться за счёт 4d-электронов, которые очень близки по энергии 4p-орбиталям. Следующий элемент — бром — является галогеном и образует анион с зарядом −1, чтобы достичь замкнутой конфигурации оболочки криптона. И наконец, завершает строку криптон, обладающий замкнутой оболочкой.

Более крупные атомы и лантаноиды с актиноидами

Элементы в пятой строке Периодической таблицы следуют той же схеме, что и в четвёртой строке. В пятой строке содержится вторая серия переходных металлов. Элементы шестой и седьмой строк ведут себя подобно занимающим четвёртую и пятую строки, за исключением наличия лантаноидов (первого внутреннего ряда переходных металлов) и актиноидов (второго внутреннего ряда переходных металлов). Они появляются в результате заполнения 4f- и 5f-орбиталей (см. диаграмму энергетических уровней для многоэлектронных атомов на рис. 11.1). Орбитали 4f (для лантаноидов с n=4) и 5f (для актиноидов с n=5) геометрически гораздо меньше орбиталей 6s и 6p, 7s и 7p (с n=6 и n=7), которые заполняются в шестой и седьмой строках, поскольку у них меньше главное квантовое число n. Самые внешние электроны (с наибольшим главным квантовым числом) определяют химические свойства атомов, то есть число валентных связей, которые они могут создавать, или ионов, которые они могут образовывать. Поэтому 4f- и 5f-орбитали не оказывают существенного влияния на химические свойства.

Лантаноиды начинаются с лантана (La). Энергетические уровни 4f расположены очень близко по энергии к уровням 5d (см. рис. 11.1). La следует за барием (Ba), у которого имеется два электрона на 6s-орбитали. У La на один электрон больше; этот электрон располагается на 5d-орбитали. Вслед за La заполняются 4f-орбитали. Лютеций (Lu, 71-й элемент) начинает третий ряд переходных металлов. У него два электрона на 6s-орбитали, 14 электронов на 4f-орбиталях и один электрон на 5d-орбитали. По химическим свойствам все лантаноиды очень похожи на La и Lu. Аналогичным образом актиноиды начинаются с актиния (Ac). После заполнения 5f-орбиталей 14 электронами лоуренсий (Lr, искусственно созданный 103-й элемент) начинает пятый ряд переходных металлов. Все актиноиды по химическим свойствам очень похожи на Ac и Lr.

Большинство элементов — металлы

В Периодической таблице используется цветовая разметка (разный тон клеток на рис. 11.4), выделяющая металлы, полуметаллы (полупроводники) и неметаллы (изоляторы). (Подробно квантовая теория, объясняющая, почему разные вещества являются металлами, полупроводниками или изоляторами, описывается в главе 19.) Из Периодической таблицы видно, что большинство элементов — это металлы. Нетрудно понять, почему это так. Элементы двух левых столбцов являются металлами, поскольку имеют один или два электрона сверх замкнутой электронной оболочки предшествующего благородного газа. Они легко могут отдать эти электроны и вернуться к замкнутой конфигурации оболочки. Поэтому когда эти вещества находятся в твёрдой форме, электроны в них подвижны, и они являются проводниками электричества. Добавление d-электронов в переходных рядах не отнимает у элементов эту способность отдавать самые внешние (с наибольшим n) s-электроны. Наличие d-электронов лишь увеличивает число электронов, которые могут быть отданы при определённых обстоятельствах. Добавление f-электронов также ничего не меняет. Поэтому в дополнение к двум левым столбцам таблицы все переходные ряды элементов являются металлами — обычно их называют переходными металлами.

Внутренние переходные ряды (в которых добавляются f-электроны) тоже являются металлами. Элементы, которые могут отдать три электрона, чтобы вернуться к предшествующей замкнутой конфигурации оболочки, такие как алюминий, также являются металлами. Вместе все они составляют большинство элементов. Неметаллы — это группа элементов в треугольной правой верхней части Периодической таблицы. Некоторые из них склонны образовывать ковалентные связи путём совместного использования электронов. Они не склонны отдавать электроны. Галогены предпочитают присоединять электроны или образовывать ковалентные связи. А благородные газы, в общем и целом, не желают ни присоединять, ни отдавать электроны, ни образовывать ковалентные связи. Таким образом, все эти элементы являются неметаллами. Когда эти вещества находятся в твёрдом состоянии, их атомы не склонны отдавать электроны, что необходимо для обеспечения электрической проводимости. Они являются изоляторами.

Элементы небольшой группы, образующей диагональную полосу в правой части Периодической таблицы, называются полуметаллами, или полупроводниками. При некоторых условиях они могут проводить электричество. Из всех полупроводников наиболее известен и технологически значим кремний. Он широко используется в микроэлектронике — в компьютерах и других цифровых устройствах. В главе 19 мы обсудим разницу между металлами, изоляторами и полупроводниками, опираясь на представления теории молекулярных орбиталей, которая описывается в главе 12 и подробнее рассматривается в последующих главах.

В этой главе мы использовали многоэлектронную диаграмму энергетических уровней (см. рис. 11.1) и правила заполнения атомных орбиталей (принцип Паули, приоритет наименьшей энергии, правило Хунда) для обсуждения Периодической таблицы. Было показано, что очень простые соображения позволяют далеко продвинуться в понимании свойств элементов и некоторых аспектов образования химических связей в молекулах. Однако мы пока не использовали идеи квантовой теории для обсуждения природы химических связей и свойств молекул, например их формы, которая определяется квантовыми принципами. В главе 12 мы начнём рассмотрение квантовой теории с молекулы водорода H₂ — простейшей из всех молекул.

12. Молекула водорода и ковалентная связь

Один из величайших триумфов в квантовой механике — это теоретическое объяснение ковалентной связи. Два типа взаимодействий удерживают атомы вместе: ковалентные связи и ионные связи. Ионный тип связи имеет место в кристалле хлорида натрия (NaCl). Из главы 11 и обсуждения Периодической таблицы мы знаем, что этот кристалл соли состоит из катионов натрия Na¹⁺ и анионов хлора Cl¹⁻. Ионы в кристалле удерживаются вместе электростатическим взаимодействием. Противоположные заряды притягиваются. Некоторые трудности возникают в связи с тем, что одинаковые заряды отталкиваются, но можно показать, что притяжение противоположно заряженных ионов превосходит отталкивание одинаково заряженных ионов. Такие электростатические взаимодействия можно в общих чертах описать на основе классической механики, хотя квантовая механика всё равно необходима для объяснения многих деталей.

В отличие от ионного типа связи в кристаллах, которые скрепляются электростатическим взаимодействием, ковалентную связь классическая механика объяснить не может. В главе 11 мы узнали, что атом водорода имеет тенденцию образовывать ковалентную связь с другим атомом для совместного использования одного электрона. Это совместное использование наделяет атом H замкнутой конфигурацией электронной оболочки гелия. Но что представляет собой ковалентная связь? Почему атомы водорода совместно используют электроны, образуя молекулу H₂, а атомы гелия не используют электроны совместно для образования молекулы He₂? Сначала мы рассмотрим природу ковалентной связи на примере простейшей молекулы H₂, а затем, в последующих главах, расширим обсуждение ковалентной связи на более сложные молекулы. К концу этой главы станет ясно, почему существует молекула H₂, но нет молекулы He₂.

Два атома водорода, находящихся далеко друг от друга

Два атома водорода, назовём их a и b, не взаимодействуют, когда они значительно удалены друг от друга. Если расстояние между ними велико, то электрон атома водорода a будет чувствовать лишь кулоновское притяжение протона атома a. Электрон атома водорода b будет взаимодействовать только с протоном атома b. Теперь мы знаем, как описывать разделённые атомы водорода. Пусть оба они находятся в своём низшем энергетическом состоянии 1s. Электрон описывается волновой функцией 1s, которая представляет собой атомную орбиталь. Она определяет амплитуду вероятности обнаружить электрон в данной области пространства. Квадрат волновой функции показывает вероятность обнаружить электрон. Состояние 1s для атома водорода достаточно подробно обсуждалось в главе 10 (см. рис. 10.2–10.4).

Два атома водорода сближаются

Теперь рассмотрим, что случится, когда мы станем постепенно приближать друг к другу атомы водорода. Когда они сблизятся, но не слишком сильно, то начнут чувствовать друг друга. Ниже мы оценим это расстояние количественно. Электрон в атоме водорода a начнёт чувствовать притяжения протона атома b и отталкивание электрона атома b. Точно так же электрон атома водорода b притягивается протоном атома a и отталкивается электроном того же атома. Кроме того, положительно заряженные протоны атомов a и b отталкиваются друг от друга, поскольку имеют одинаковый заряд.

Можно решить уравнение Шрёдингера для данной задачи. Хотя это нельзя сделать строго, точность может быть очень высокой. Что даёт нам это решение уравнение Шрёдингера? Оно даёт энергетические уровни системы и её волновые функции. Когда мы решали задачу о частице в ящике, мы получили волновую функцию одиночной частицы в гипотетическом одномерном ящике с бесконечно высокими стенками. В случае уравнения Шрёдингера для атома водорода или других атомов мы получаем энергетические уровни и атомные волновые функции — атомные орбитали. Решая молекулярную задачу, мы получаем квантованные значения энергии для молекулярных энергетических уровней и молекулярные волновые функции. Последние обычно называют молекулярными орбиталями. Таким образом, для атомов мы получаем атомные орбитали, описывающие распределение вероятности обнаружения электрона вокруг атомного ядра. Это волна амплитуды вероятности. Молекулярная орбиталь описывает распределение вероятности обнаружения электронов в молекуле вокруг ядер тех атомов, из которых состоит молекула. У молекулы водорода имеется два электрона и два атомных ядра — два протона.

Приближение Борна-Оппенгеймера

Очень хороший способ понять, как связываются атомы водорода, когда они сближаются и образуют молекулу водорода, основывается на концепции, известной как приближение Борна-Оппенгеймера. Как говорилось в главе 5, Борн получил Нобелевскую премию по физике в 1954 году за свою вероятностную интерпретацию волновой функции. Оппенгеймер внёс большой вклад в физику. Наибольшую известность он получил как физик, руководивший во время Второй мировой войны Манхэттенским проектом, в рамках которого разрабатывалась и испытывалась первая атомная бомба. В приближение Борна-Оппенгеймера требуется поместить два ядра атомов водорода (два протона) на фиксированном расстоянии друг от друга. Начнём с расстояния, которое вы сочтёте достаточно большим, чтобы атомы водорода не чувствовали друг друга. Выполним квантовомеханический расчёт энергии. Если атомы находятся далеко друг от друга, то эта энергия будет равна просто удвоенной энергии атома водорода в 1s-состоянии, поскольку имеется всего два атома водорода. Теперь немного уменьшим расстояние и повторим вычисления, а потом ещё уменьшим расстояние и вновь выполним вычисления. Когда расстояние между ядрами в нашем расчёте станет достаточно малым, атомы почувствуют друг друга. Если должна образоваться химическая связь, то есть если два атома водорода собираются объединиться в молекулу водорода, то энергия должна убывать. Для образования связи энергия молекулы должна быть меньше, чем энергия атомов, когда они разнесены далеко друг от друга.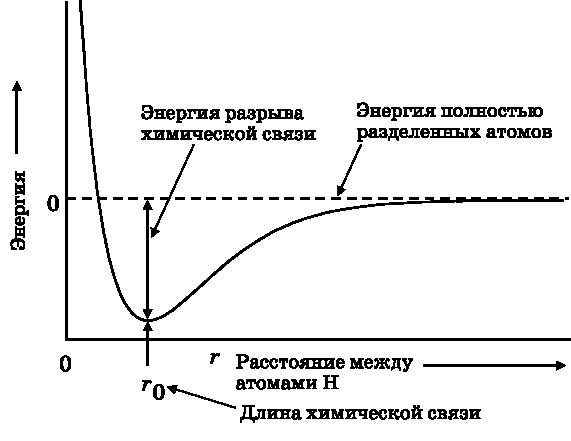

Рис. 12.1. График зависимости энергии двух атомов водорода от расстояния между ними. Когда два атома H находятся очень далеко друг от друга, энергия системы равна сумме энергий 1s-орбиталей двух атомов H. Эта величина принимается за нулевое значение энергии, отмеченное штриховой линией. При сближении атомов энергия убывает, пока не достигает минимума. Если атомы сближаются ещё сильнее, энергия быстро возрастает

На рис. 12.1 представлен график изменения энергии двух атомов водорода в процессе их сближения друг с другом. Как уже отмечалось, когда два атома водорода находятся очень далеко друг от друга, они не взаимодействуют. Каждый из них имеет энергию, соответствующую 1s-орбитали атома водорода. Будем считать это нулевым уровнем энергии. Сам по себе атом водорода имеет отрицательную энергию, как это объяснялось в главе 10. Эта энергия соответствует энергии связи электрона с протоном (ядром). Сейчас нас интересует изменение энергии, когда два атома водорода вступают во взаимодействие. Мы хотим найти энергию, ассоциированную с химической связью, поэтому нулевая энергия — это та, при которой химическая связь отсутствует. На рис. 12.1 нулевая энергия обозначена штриховой линией. Это энергия, соответствующая состоянию, когда атомы полностью разделены. По горизонтальной оси отложено расстояние r между двумя атомами H. По мере сближения атомов H энергия начинает убывать, причём всё быстрее и быстрее. Она достигает минимума при расстоянии между атомами r₀ (см. рис. 12.1). Если атомы сближаются ещё сильнее, энергия очень быстро возрастает, то есть когда атомы находятся слишком близко, они отталкиваются друг от друга. Поскольку при сближении двух атомов энергия убывает, между ними образуется химическая связь.

Длина химической связи — это расстояние, которое обеспечивает наименьшую энергию

На расстоянии r₀ энергия достигает минимума. Это расстояние между атомами H является наиболее устойчивым (обладает наименьшей энергией). Оно называется длиной химической связи. Это расстояние между двумя протонами в устойчивой молекуле водорода. Разность между дном энергетической «потенциальной ямы» и нулевой энергией составляет энергию разрыва химической связи (энергию диссоциации). Она равна количеству энергии, которую надо передать молекуле водорода, чтобы разорвать химическую связь и получить два отдельных атома водорода. Потенциальная яма для молекулы водорода подобна яме в земле, в которую скатывается мяч. Вне ямы энергия равна нулю. Мяч падает на дно ямы, чтобы минимизировать гравитационную потенциальную энергию. Гравитация тянет мяч вниз. Чтобы поднять мяч из потенциальной ямы, требуется энергия, поскольку нужно преодолеть гравитационное притяжение, действующее на мяч. Чем глубже яма, тем больше энергии потребуется, чтобы поднять из неё мяч. В случае с молекулами чем глубже потенциальная яма, тем больше энергии нужно, чтобы из неё выбраться, то есть разорвать химическую связь.

На рис. 12.1 не показана шкала расстояний по оси r. Интересно, однако, рассмотреть два расстояния. На какой дистанции атомы водорода впервые начинают ощущать присутствие друг друга? На рис. 10.3 видно, что волна амплитуды вероятности для 1s-орбитали атома водорода становится очень малой на расстоянии от ядра около 3 Å (3∙10⁻¹⁰ м). Так что можно ожидать, что два атома водорода начнут взаимодействовать, если сойдутся чуть ближе 6 Å. На рис. 12.1 точка, где кривая потенциальной энергии (сплошная линия) начинает отклоняться от линиинулевой энергии (штриховая прямая), находится примерно на 6 Å, так что атомы начинают чувствовать друг друга, как только у их атомных волновых функций возникает существенное перекрытие. Точка r₀ — это положение минимума на кривой потенциальной энергии. Она соответствует длине химической связи. Эксперименты и расчёты показали, что это расстояние составляет 0,74 Å. Если расстояние между атомами больше или меньше этого значения, энергия будет выше.

Кривая потенциальной энергии, изображённая на рис. 12.1, получена на основе реальных квантовомеханических расчётов. Это относительно несложные вычисления, которые можно целиком выполнить с помощью карандаша и бумаги, компьютеры для этого не нужны. По результатам приближённых вычислений r₀=0,80 Å, так что они не вполне точны. Если хотите увидеть огромный объём математических выкладок, которые требуются даже для этого относительно простого расчёта, загляните в главу 17 моего учебника основ квантовой механики (Michael D. Fayer. Elements of Quantum Mechanics. New York: Oxford University Press, 2001). Намного более сложные квантовые теоретические вычисления для молекулы H₂ позволяют получить все свойства молекулы водорода с точностью выше достижимой в экспериментальных измерениях. Точные вычисления возможны благодаря тому, что молекула водорода очень проста. Для крупных молекул эксперименты всё ещё превосходят вычисления по точности.

Образование связывающих молекулярных орбиталей

Из рис. 12.1 видно, что между двумя атомами водорода будет формироваться химическая связь, в результате чего образуются молекулы H₂, но неясно, каким образом. Как отмечалось в главе 11, ковалентная связь состоит в том, что атомы совместно используют электроны. Когда образуется молекула, атомные орбитали объединяются и формируют молекулярные орбитали. Для молекулы водорода мы начнём с двух атомов водорода: H_a и H_b. Каждый из них имеет один электрон атомной 1s-орбитали. Обозначим эти орбитали 1s_a и 1s_b. В верхней части рис. 12.2 они показаны кружками. Это простое схематическое изображение делокализованной волны амплитуды вероятности электрона, представленной на рис. 10.2-10.4. В нижней части рисунка показано, что происходит, когда два атома сближаются так, что расстояние между ними становится равным длине химической связи r₀ (см. рис. 12.1). Волновые функции имеют знак. В данном случае их знаки положительные.

Рис. 12.2. Вверху схематически изображены две 1s-орбитали атомов водорода. В действительности это делокализованные волны амплитуды вероятности электронов, изображённые здесь в виде окружностей. В нижней части рисунка показано, что происходит, когда два атома сближаются и образуют молекулу H ₂ . Две атомные орбитали объединяются и образуют молекулярную орбиталь

Волны амплитуды вероятности складываются и образуют молекулярную орбиталь. Мы довольно подробно обсуждали волны в главах 3 и 5. В главе 3 мы узнали, что волны при объединении могут давать конструктивную и деструктивную интерференцию. В главе 5 интерференция фотонов объяснялась через борновскую интерпретацию волновой функции как волны амплитуды вероятности. Теперь две волны амплитуды вероятности электрона, представляющие собой атомные орбитали, объединяются и в результате конструктивной интерференции образуют молекулярную орбиталь. Молекулярная орбиталь — это волна амплитуды вероятности. Возведённое в квадрат её абсолютное значение даёт вероятность обнаружения электронов в определённой области пространства.

Рис. 12.3. Одномерный график квадратов двух 1s-орбиталей, принадлежащих атомам водорода: a и b (сплошные кривые), и квадрата суммы атомных орбиталей, который является квадратом молекулярной орбитали. Электронная плотность концентрируется между двумя ядрами

На рис. 12.3 представлен одномерный график распределения вероятности (квадрата волновой функции) для двух атомных орбиталей (1s_a и 1s_b) и квадрат суммы атомных орбиталей. В центре атомных орбиталей находятся ядра атомов H, которые разделены расстоянием, равным длине химической связи r₀. Протоны (ядра) заряжены положительно и отталкиваются друг от друга. Однако молекулярная орбиталь концентрирует между ядрами электронную плотность, несущую отрицательный заряд, и тем удерживает их вместе. Важная особенность молекулярной орбитали состоит в том, что электроны больше не принадлежат одному или другому атому. Молекулярная орбиталь описывает делокализованное распределение вероятностей для двух электронов. Оба электрона свободно перемещаются по всей молекуле. Электроны, принадлежавшие разным атомам, когда те находились далеко друг от друга, теперь принадлежат всей молекуле. Они совместно используются атомами, которые больше не являются независимыми.

Связывающие и разрыхляющие молекулярные орбитали

До сих пор за рамками нашего обсуждения оставался один очень важный вопрос. Принцип Паули (см. главу 11) утверждает, что на любой орбитали может находиться максимум два электрона. Для образования молекулы водорода мы начинаем с двух атомов водорода. Каждый такой атом имеет 1s-орбиталь. Согласно принципу Паули, на эти две орбитали можно поместить четыре электрона. У двух атомов водорода имеется только два электрона, но принцип Паули не нарушился бы, если бы на каждую атомную 1s-орбиталь добавили ещё по одному электрону. Мы сложили две 1s-орбитали и за счёт конструктивной интерференции получили одну молекулярную орбиталь. Принцип Паули гласит, что на эту молекулярную орбиталь можно поместить максимум два электрона. Мы начали с двух атомных орбиталей, которые содержат четыре электрона, но теперь у нас одна молекулярная орбиталь, которая может содержать два электрона. Чего-то явно не хватает. При образовании молекул места для электронов (орбитали) никогда не исчезают и не появляются. Если было две атомные орбитали, то должны образоваться две молекулярные орбитали, способные содержать четыре электрона.

На рис. 12.2 и 12.3 две атомные 1s-орбитали водорода складывались с одинаковым знаком и давали молекулярную орбиталь, которая концентрирует электронную плотность между двумя атомными ядрами. Эти 1s-орбитали являются волнами амплитуды вероятности и могут также складываться с противоположными знаками. При таком сложении атомные орбитали интерферируют деструктивно. Сложение с противоположными знаками изображено на рис. 12.4. Поскольку знаки двух атомных орбиталей противоположны, должно быть место, где положительная волна в точности гасит отрицательную волну. Это узел, подобный тем, что мы ранее обсуждали для волновой функции частицы в ящике и атомных орбиталей. Как видно из схемы на рис. 12.4, деструктивная интерференция между атомными орбиталями и получающиеся в результате узлы выталкивают электронную плотность из пространства между атомными ядрами. Отрицательно заряженные электроны больше не экранируют положительно заряженные ядра, которые отталкиваются. В отличие от кривой, полученной для сближения двух атомов водорода (см. рис. 12.1), в этом случае энергия не уменьшается, а возрастает.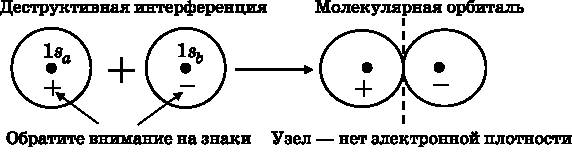

Рис. 12.4. Слева схематически изображены две атомные 1s-орбитали водорода, которые будут складываться. Обратите внимание, что волны амплитуды вероятности имеют противоположные знаки. Две атомные орбитали объединяются и дают молекулярную орбиталь. В отличие от рис. 12.2 из-за противоположности знаков возникает деструктивная интерференция

Образующаяся при конструктивной интерференции атомных 1s-орбиталей молекулярная орбиталь (см. рис. 12.2 и 12.3), которая ответственна за химическую связь в молекуле H₂, называется связывающей молекулярной орбиталью (МО). Молекулярная орбиталь, образующаяся при деструктивной интерференции между атомными орбиталями, называется разрыхляющей МО^{19}, поскольку она не даёт вклада в химическую связь, а, наоборот, увеличивает энергию атомов при их сближении.

На рис. 12.5 схематически изображены энергетические кривые для связывающий и разрыхляющей молекулярных орбиталей в молекуле H₂. Как говорилось, когда обсуждался рис. 12.1, при сближении двух атомов водорода энергия убывает и достигает минимума, прежде чем вновь начать возрастать. Это кривая связывающей МО. Напротив, кривая разрыхляющей МО показывает, что энергия начинает расти, как только два атома сближаются настолько, чтобы почувствовать друг друга. Энергия продолжает возрастать по мере сближения атомов. Она нигде не убывает. Если электроны находятся на разрыхляющей МО, два атома не будут образовывать химические связи, поскольку энергия состоящей из них системы всегда выше энергии отдельных атомов.

Рис. 12.5. Схематическое представление кривых зависимости энергии от расстояния для связывающей и разрыхляющей молекулярных орбиталей при сближении двух атомов водорода. В отличие от связывающей МО энергия разрыхляющей МО возрастает при уменьшении расстояния между атомами

Расселение электронов по молекулярным орбиталям

Мы начали с двух атомных орбиталей: 1s_a и 1s_b, связанных с двумя атомами водорода — H_a и H_b. Эти две атомные орбитали порождают две молекулярные орбитали — связывающую и разрыхляющую. Правила, которыми мы пользовались для заполнения атомных орбиталей электронами, применимы и здесь. Принцип Паули говорит, что на одной МО может располагаться не более двух электронов и они должны иметь противоположные спины (спины спариваются: одна стрелка вверх, другая вниз). Электроны занимают сначала низшие энергетические уровни, но так, чтобы не нарушался принцип Паули. Правило Хунда утверждает, что электроны будут неспаренными, если это не нарушает первые два правила. Правило Хунда не потребуется нам до следующей главы, где будут обсуждаться крупные молекулы. Теперь мы готовы к тому, чтобы разобраться, почему существует молекула водорода H₂, но не существует молекулы гелия He₂.

Молекула водорода есть, а молекулы гелия нет

При расстоянии между атомами, соответствующем длине химической связи, то есть при том расстоянии, которое обнаруживается в реальной молекуле, связывающая МО по энергии всегда ниже, чем отдельные атомы, а разрыхляющая МО всегда выше. Это строгий результат, вытекающий из законов квантовой механики. Будет хорошей аппроксимацией сказать, что уменьшение энергии на связывающей МО равно увеличению энергии на разрыхляющей МО.

На рис. 12.6 представлена простая диаграмма, показывающая, как атомные орбитали объединяются и образуют молекулярные орбитали. Мы будем использовать такого рода диаграммы в последующих главах. Две атомные 1s-орбитали — по одной для каждого атома H — изображены на рисунке слева и справа. Линии, проходящие через них, — это нулевой уровень энергии для молекулярных орбиталей, то есть эти линии соответствуют энергии атомов, когда они разнесены так далеко, что не чувствуют друг друга. В центре изображены энергетические уровни связывающей и разрыхляющей МО. Они обозначены σ^b в случае связывающей орбитали (b — от англ. bonding) и σ^* в случае разрыхляющей орбитали. Греческой буквой сигма (σ) обозначается особый тип связи, называемый σ-связью, который будет обсуждаться в главе 13. Штриховые линии, соединяющие атомные орбитали с МО, показывают, что обе атомные орбитали объединяются и дают две МО, когда атомы образуют молекулу.

Рис. 12.6.Диаграмма энергетических уровней, представляющая объединение двух атомных 1s-орбиталей в связующую и разрыхляющую МО, когда атомы находятся на расстоянии, равном длине химической связи r₀, которое соответствует энергетическому минимуму для связывающей МО. Связывающая МО ниже по энергии, чем атомные орбитали, а разрыхляющая МО настолько же выше по энергии. Связывающая МО обозначается σ^b, а разрыхляющая МО — σ^*

Диаграмма энергетических уровней МО, приведённая на рис. 12.6, показывает два энергетических состояния, участвующих в образовании молекулы водорода. Однако мы ещё не произвели «заселение» двух электронов. Данная диаграмма аналогична диаграмме энергетических уровней многоэлектронного атома (см. рис. 11.1). Нам даны энергетические уровни, но для понимания того, что получится, нужно ещё расселить по ним электроны. Имеется два электрона — по одному от каждого атома водорода. Мы знаем, что электроны размещаются на самом нижнем доступном энергетическом уровне до тех пор, пока число электронов не нарушает принцип Паули, то есть на каждой орбитали может находиться максимум два электрона со спаренными спинами. Это применимо к МО так же, как и к атомным орбиталям.

На рис. 12.7 представлена диаграмма энергетических уровней МО с двумя электронами (обозначены стрелками). Два электрона занимают низший энергетический уровень σ^b и имеют спаренные спины. Когда атомы разнесены далеко, электроны имеют энергию, соответствующую линиям атомных 1s-орбиталей. Связывающая МО имеет существенно более низкую энергию. Именно это уменьшение энергии обеспечивает целостность молекулы. Два электрона находятся на молекулярной орбитали. Ни один из них не связан с конкретным атомом. Ковалентная связь состоит в совместном использовании электронов атомами.

Рис. 12.7. Диаграмма МО молекулы водорода. Два электрона (стрелки), по одному от каждого атома водорода, занимают низший энергетический уровень, а их спины спарены. Их энергия ниже, чем у отдельных атомов. Тем самым за счёт совместного использования электронов образуется связь

Почему не существует молекулы гелия He₂? У каждого из двух отдельных атомов He на 1s-орбитали имеется по два электрона. Поэтому диаграмма МО будет такой же, как на рис. 12.6. Однако теперь нам необходимо расселить по энергетическим уровням МО четыре электрона. На рис. 12.8 представлена диаграмма МО с четырьмя электронами. Первый электрон заселяется на связывающую МО, поскольку это низшее энергетическое состояние. Второй электрон также попадает на связывающую МО со спином, противоположным первому. Принцип Паули гласит, что ни у каких двух электронов не могут совпадать все квантовые числа. Два электрона на связывающей МО имеют разные спиновые квантовые числа: s=+½ и s=−½. Существуют только эти два значения спинового квантового числа, так что третий электрон не может попасть на связывающую МО. Он должен занять следующий энергетический уровень, который представлен разрыхляющей МО. Четвёртый электрон также может заселиться на разрыхляющую МО с противоположным спином. Два электрона на связывающей МО имеют энергию ниже, чем в отдельных атомах, но два электрона на разрыхляющей МО повышают энергию ровно настолько, насколько связывающие электроны её понижают. В результате не возникает никакого уменьшения энергии в сравнении с отдельными атомами. Целостность молекулы обеспечивается тем, что связанные атомы имеют более низкую энергию, чем отдельные атомы. В случае атомов гелия уменьшения энергии, которое привело бы к образованию устойчивой конфигурации, не происходит, и поэтому связь не возникает. В следующей главе мы познакомимся с аналогичным поведением благородного газа неона.

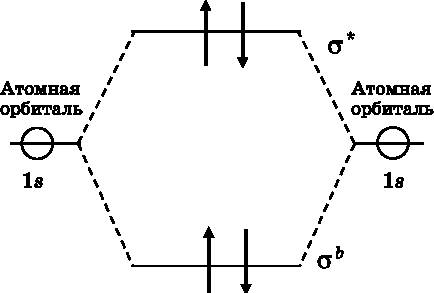Рис. 12.8. Диаграмма МО гипотетической молекулы гелия. Имеется четыре электрона (стрелки), по два от каждого атома гелия. Два из них занимают связывающую МО. Два других в силу принципа Паули отправляются на разрыхляющую МО. В целом уменьшения энергии не происходит, и поэтому связь не возникает

Чтобы оценить прогностические возможности простых диаграмм, таких как изображённые на рис. 12.7 и 12.8, рассмотрим четыре возможные молекулы. Это молекулярный ион водорода H₂⁺, молекула водорода H₂, молекулярный ион гелия He₂⁺ и молекула He₂. Молекулярный ион H₂⁺ состоит из двух ядер водорода (протонов) и одного электрона. Подобно одноатомному катиону Na⁺, он является положительно заряженным, поскольку электронов у него на один меньше, чем протонов. He₂⁺ — это молекулярный ион, состоящий из двух ядер гелия (по два протона в каждом) и трёх электронов. Таким образом, в нём имеется четыре положительно заряженных частицы (четыре протона) и три отрицательно заряженных электрона.

На рис. 12.9 представлена диаграмма энергетических уровней МО для этих четырёх молекул. Атомные энергетические уровни опущены. Молекулярный ион H₂⁺ имеет только один электрон, так что он занимает самый нижний энергетический уровень — связывающую МО. Энергия получается ниже, чем у разделённых атомов, но лишь на величину, примерно вдвое меньшую, чем у молекулы H₂, которая имеет два электрона на связывающей МО. Молекула H₂ обладает полной ковалентной связью. Говорят, что она имеет порядок связи, равный 1. Молекулярный ион H₂⁺ имеет порядок связи, равный ½.

Рис. 12.9.Диаграмма энергетических уровней МО для четырёх молекул: молекулярного иона водорода H₂⁺, молекулы водорода H₂, молекулярного иона гелия He₂⁺и молекулы He₂

Молекулярный ион He₂⁺ имеет три электрона. Первые два из них находятся на связывающей МО, но в силу принципа Паули третий электрон должен размещаться на разрыхляющей МО. Два электрона понижают энергию относительно раздельных атомов, но третий электрон повышает эту энергию. В целом имеет место уменьшение энергии. Молекулярный ион He₂⁺ существует в природе и имеет порядок связи, равный ½. Как уже говорилось, молекула He₂ имеет два связывающих электрона и два разрыхляющих электрона. Связь не возникает, то есть порядок связи равен нулю. Молекулы He₂ не существует.

В табл. 12.1 содержится количественная информация об этих четырёх молекулах. В ней приводятся число связывающих электронов, число разрыхляющих электронов и итоговый результат, равный разности числа связывающих электронов и числа разрыхляющих. В таблице также приводится порядок связи. Последние две колонки особенно интересны.

Таблица 12.1.Свойства молекулярного иона водорода H₂⁺, молекулы водорода H₂, молекулярного иона гелия He₂⁺ и молекулы He₂

Связ. электроны, Разр. электроны, Разность, Порядок связи, Длина связи, Энергия связи

H₂: 2; 0; 2; 1; 0,74Å; 7,2∙10⁻¹⁹Дж

H₂⁺: 1; 0; 1; ½; 1,06Å; 4,2∙10⁻¹⁹Дж

He₂⁺: 2; 1; 1; ½; 1,08Å; 5,4∙10⁻¹⁹Дж

He₂: 2; 2; 0; 0; Нет; Нет

Данные, приведённые в табл. 12.1, — это результаты экспериментальных измерений. Прежде всего, остановимся на длине химической связи. Она выражена в ангстремах (1 Å = 10⁻¹⁰ м). Молекулярный ион H₂⁺ имеет связь порядка ½ и длину химической связи 1,06 Å. Для сравнения отметим, что молекула H₂ имеет полноценную связь порядка 1 и длину химической связи 0,74 Å. Дополнительный электрон на связывающей МО в молекуле H₂ удерживает атомы крепче и потому теснее. Молекулярный ион He₂⁺ имеет связь порядка ½ и длину химической связи 1,08 Å, которая лишь незначительно больше, чем у молекулярного иона H₂⁺. Конечно, He₂ — это не молекула и поэтому не имеет химической связи. В последнем столбце приведена энергия связи в единицах 10⁻¹⁹ Дж. Интересна относительная сила связи. Молекула H₂ со связью порядка 1 имеет существенно бо́льшую энергию связи, чем два молекулярных иона, в которых порядок связи составляет ½. Так простые диаграммы МО позволяют узнать, будет ли существовать связь, и дают информацию о том, насколько сильной она окажется.

В этой главе мы воспользовались представлениями о молекулярных орбиталях для рассмотрения простейших молекул. Обсуждение касалось только атомов, содержащих 1s-электроны. Все остальные атомы и молекулы содержат больше электронов и больше орбиталей. В следующей главе представленные здесь идеи будут использоваться для анализа двухатомных молекул, включающих более крупные атомы, такие как молекула кислорода O₂ и молекула азота N₂. Эти две молекулы являются основными составляющими воздуха, которым мы дышим.

13. Что удерживает атомы вместе: двухатомные молекулы

Молекула водорода является двухатомной, то есть состоит лишь из двух атомов. В процессе изучения водорода мы обнаружили, что атомы могут объединять свои атомные орбитали, образуя молекулярные орбитали. Нам предстоит расширить обсуждение молекулярных орбиталей, с тем чтобы понять, как из атомов образуются более сложные молекулы. Начнём мы с рассмотрения других двухатомных молекул на примере N₂, O₂, F₂ и HF. Молекулы N₂, O₂ и F₂ (азот, кислород и фтор) называются гомонуклеарными, поскольку состоят из одинаковых атомов. Молекула HF (фтороводород) — гетеронуклеарная, поскольку два её атома различны. Анализ гомонуклеарных двухатомных молекул выведет нас за рамки того, что мы узнали о молекуле водорода, которая является частным случаем. Изучение природы молекулярных орбиталей в гетеронуклеарных двухатомных молекулах — это важный шаг вперёд к пониманию многоатомных молекул, из которых состоит большинство окружающих нас молекулярных веществ — от спирта до жиров.

Молекула водорода — единственная нейтральная молекула, в которой для образования химических связей служат только электроны, находящиеся на 1s-обитателях. Электроны, используемые атомами для связывания между собой, называются валентными. В молекулах N₂, O₂, F₂ и HF в образование связей вовлечены орбитали 2s и 2p. 2s- и 2p-электроны являются валентными электронами. Атомы N, O, и F расположены во второй строке Периодической таблицы. У атомов из третьей строки Периодической таблицы, таких как P, S и Cl (фосфор, сера и хлор), связывание обеспечивается валентными 3s- и 3p-электронами. Атомы из третьей и последующих строк Периодической таблицы могут также использовать для образования химических связей d-электроны. Здесь мы сконцентрируемся на очень важных элементах второй строки, но идеи, с которыми мы познакомимся, обладают значительной общностью и охватывают природу химических связей более тяжёлых элементов.

Сигма-связи (σ) и пи-связи (π)

Как показано на рис. 12.2, когда два атома водорода образуют молекулу H₂, две 1s-орбитали водорода объединяются и формируют связывающую молекулярную орбиталь. Вдоль оси, соединяющей ядра, при этом имеется определённая электронная плотность. Связывающая и разрыхляющая молекулярные σ-орбитали (сигма-орбитали) имеют ненулевую электронную плотность вдоль линии, соединяющей ядра. Мы говорим, что в молекуле H₂ σ-связь образована с использованием связывающей молекулярной σ-орбитали. s-орбитали всегда образуют σ-связи. Не существует способа объединить две s-орбитали и не получить никакой электронной плотности вдоль линии, соединяющей ядра. Однако для p-орбиталей это не так.

С учётом формы p-орбиталей их пары могут объединяться двумя способами, представленными на рис. 13.1. Орбитали на рисунке изображены очень схематично. В действительности это волны амплитуды вероятности, задающие диффузное распределение вероятности обнаружить электрон в том или ином месте относительно ядра. Приведённые здесь контуры отражают лишь общую форму p-орбиталей. Это лучше проиллюстрировано на рис. 10.7. Напомним, что у p-орбиталей есть узловая плоскость, располагающаяся между двумя лепестками. В узловой плоскости вероятность обнаружить электрон равна нулю. Для p_z-орбитали узловой является плоскость xy (см. рис. 10.7). Вероятность обнаружить электрон в некоторой области пространства часто называют электронной плотностью. Высокая плотность означает высокую вероятность обнаружения электрона.

Рис. 13.1. Пара сблизившихся между собой p-орбиталей. Вверху: орбитали сближаются концами; вдоль линии, соединяющей ядра, имеется ненулевая электронная плотность. Внизу: орбитали сближаются боками; вдоль линии, соединяющей ядра, электронная плотность равна нулю

В верхней части рис. 13.1 изображены две орбитали, сближающиеся друг с другом концами. Их лепестки направлены друг к другу. Ядра изображены жирными точками. Штриховая прямая соединяет ядра. Очевидно, что вдоль этой прямой, соединяющей ядра, имеется ненулевая электронная плотность. В нижней части рисунка изображены 2p-орбитали, сближающиеся друг с другом боками. Узловая плоскость перпендикулярна плоскости страницы. Ядра находятся в этой узловой плоскости. Вдоль прямой, соединяющей ядра, электронная плотность равна нулю. Лепестки орбиталей имеют знак: один лепесток положительный, а другой отрицательный. На обеих схемах (см. рис. 13.1) друг с другом сближаются положительные лепестки.

Сигма-орбитали молекул

Если атомные орбитали сближаются достаточно тесно, они могут образовывать связывающие и разрыхляющие молекулярные орбитали. Сначала мы рассмотрим образуемые атомными s- и p-орбиталями связывающие и разрыхляющие молекулярные σ-орбитали. У таких орбиталей имеется отличная от нуля электронная плотность вдоль линии, соединяющей ядра. Как уже говорилось, s-орбитали могут образовывать только σ-орбитали, поскольку имеют сферическую форму. p-орбитали тоже могут образовывать σ-МО.

На рис. 13.2 представлены связывающие и разрыхляющие σ-МО, образованные как s-орбиталями, так и p-орбиталями. В верхней части рисунка изображены два возможных способа объединения s-орбиталей. s-орбитали — это волны, и с ними может быть связан либо знак «плюс», либо знак «минус». Вверху обе s-орбитали имеют знак «плюс». Когда они объединяются, волны этих s-орбиталей интерферируют конструктивно и порождают σ-связывающую МО. Ниже на рисунке одна s-орбиталь имеет знак «плюс», а другая — знак «минус». Когда они объединяются, то интерферируют деструктивно и образуют разрыхляющую МО. Связывающая МО концентрирует электронную плотность между ядрами, тогда как разрыхляющая МО выталкивает электронную плотность вовне, уменьшая несущую отрицательный заряд электронную плотность между ядрами. Положительно заряженные ядра отталкиваются сильнее, что и делает эту конфигурацию разрыхляющей.

В нижней части рис. 13.2 показаны результаты объединения двух орбиталей с получением молекулярных σ-орбиталей. σ-p-связывающие МО образуются в результате перекрытия положительных лепестков одной p-орбитали с положительными лепестками другой p-орбитали. Возникает конструктивная интерференция между положительными лепестками, создающая высокую электронную плотность между атомными ядрами. Имеются две узловые плоскости, перпендикулярные странице. Эти две узловые плоскости наследуются от двух атомных p-орбиталей. Напротив, в самом низу рисунка показано, как положительные лепестки одной p-орбитали перекрываются с отрицательными лепестками другой p-орбитали.

Рис. 13.2.Вверху: пара s-орбиталей перекрывается двумя разными способами, давая σ-связывающую (конструктивная интерференция) и σ-разрыхляющую (деструктивная интерференция) молекулярные орбитали. Внизу: пара p-орбиталей перекрывается двумя способами, давая σ-связывающую (конструктивная интерференция) и σ-разрыхляющую (деструктивная интерференция) молекулярные орбитали. Во всех случаях вдоль линии, соединяющей ядра, имеется ненулевая электронная плотность

В результате деструктивной интерференции образуется разрыхляющая МО. Электронная плотность выталкивается наружу и значительно уменьшается между двумя ядрами. В дополнение к двум узловым плоскостям, унаследованным от атомных орбиталей, появляется третья узловая плоскость, которая возникает благодаря полной деструктивной интерференции между положительным и отрицательным лепестками двух атомных p-орбиталей. У всех этих связывающих и разрыхляющих МО, образованных из атомных p-орбиталей, на линии, соединяющей ядра, электронная плотность отлична от нуля. Следовательно, это σ-МО.

Молекулярные пи-орбитали

s-орбитали могут формировать только σ-МО, но p-орбитали могут образовывать как σ-МО, так и другой тип молекулярных орбиталей, обозначаемых π (греческая буква «пи»). Когда атомные орбитали сближаются концами, они образуют σ-МО. Когда они сближаются боками, они образует π-МО (рис. 13.3).

В верхней части рисунка две p-орбитали образуют связывающую молекулярную орбиталь. Положительный лепесток одной атомной орбитали перекрывается с положительным лепестком другой, и аналогично для отрицательных лепестков. Как видно из рисунка, в области между двумя ядрами возникает значительная электронная плотность. Однако вдоль прямой, соединяющей ядра, электронная плотность равна нулю. Имеется узловая плоскость, перпендикулярная плоскости страницы, поскольку у каждой из атомных орбиталей есть такая узловая плоскость. Эта узловая плоскость проходит через ядра. Несмотря на наличие узловой плоскости, электронная плотность непосредственно над и под линией, соединяющей ядра, уменьшает отталкивание положительных ядерных зарядов. Энергия становится ниже, чем у отдельных атомов, что приводит к образованию π-связывающей МО.

В нижней части рис. 13.3 показана π-связывающая МО. Две атомные p-орбитали сближаются боками, но положительный лепесток одной орбитали перекрывается с отрицательным лепестком другой, и наоборот. Результатом становится деструктивная интерференция между лепестками, приводящая к появлению π-разрыхляющей МО. Разрыхляющая МО имеет значительно меньшую электронную плотность между ядрами. Вследствие этого энергия становится выше, чем у отдельных атомов, и поэтому такая конфигурация атомных орбиталей порождает разрыхляющую МО.

Рис. 13.3.Вверху: пара p-орбиталей перекрывается, сближаясь боками, что даёт связывающую π-орбиталь (конструктивная интерференция); вдоль линии, соединяющей ядра, электронная плотность равна нулю. Внизу: пара p-орбиталей перекрывается, сближаясь боками, с образованием разрыхляющей π-орбитали (деструктивная интерференция). Обратите внимание на знаки лепестков атомных p-орбиталей. У разрыхляющей МО имеется узловая плоскость, проходящая между ядрами

Связи в двухатомных молекулах: молекула фтора

Теперь мы готовы к обсуждению связей в двухатомных молекулах с атомами, отличными от водорода. Начнём с двухатомной молекулы фтора F₂. Будем использовать тот же подход, что применялся для H₂, но теперь имеется больше орбиталей, и в дело вовлечено больше электронов. Представим, что мы сближаем два атома F и останавливаемся в точке с наименьшей энергией. Это расстояние, на котором два атома F удерживаются, когда они связаны (в предположении, что они образуют связь), как на рис. 12.5. Можно нарисовать диаграмму энергетических уровней, как на рис. 12.6. Необходимо определить ось, вдоль которой будут сближаться атомы, поскольку у них имеются p_z-, p_x- и p_y-орбитали. Необходимо учитывать, сближаются p-орбитали концами или боками. Когда два атома (обозначим их a и b) сближаются вдоль оси z (рис. 13.4), p_z-орбитали встречаются концами, а p_x- и p_y-орбитали — боками. Поэтому атомные p_z-орбитали будут образовывать σ-МО, а p_x- и p_y-орбитали — π-МО.

Рис. 13.4. Два атома сближаются вдоль оси z. При этом p _z -орбитали будут сближаться концами, а p _x - и p _y - орбитали — боковыми сторонами

На рис. 13.5 представлена диаграмма энергетических уровней для двух атомов F, сблизившихся вдоль оси z. На этой диаграмме энергетические уровни атомных орбиталей двух атомов (a и b) изображены справа и слева, а соответствующие связывающие и разрыхляющие (*) МО показаны в середине. σ-MO, образованные атомными s-орбиталями, имеют индекс s; σ-MO, образованные атомными p_z-орбиталями, имеют индекс z, а π-МО, образованные атомными орбиталями p_x и p_y, имеют индексы x и y. Связывающие МО всегда ниже по энергии, чем атомные орбитали, которыми они образованы, а разрыхляющие МО всегда имеют более высокую энергию. Три атомные p-орбитали имеют одинаковую энергию. Когда квантовые состояния обладают одинаковой энергией, говорят, что они вырождены. На диаграмме три атомные p-орбитали, хотя они являются вырожденными, изображены тремя отдельными близко расположенными линиями. Как показано, только соответствующие друг другу атомные орбитали с одинаковой энергией объединяются в МО. Этот результат вытекает из квантовой теории.

Рис. 13.5.Диаграмма энергетических уровней для двух атомов a и b, сблизившихся до образования молекулярных орбиталей. Энергии атомных орбиталей показаны справа и слева. Энергетические уровни связывающих (b) и разрыхляющих (*) МО изображены посередине. Существуют σ- и π-МО. Три атомные p-орбитали обладают одинаковыми энергиями. Они показаны тремя близко расположенными линиями. Интервалы между уровнями показаны без соблюдения масштаба

Состояния с одинаковой энергией легко могут объединяться и порождать состояния суперпозиции. В данном случае атомные орбитали с одинаковой энергией в двух разных атомах могут объединяться и создавать молекулярные орбитали. В общем случае только атомные состояния с близкой энергией могут объединяться в МО. Это будет важно, когда мы перейдём к обсуждению гетеронуклеарных двухатомных молекул. В гомонуклеарных двухатомных молекулах атомные орбитали обладают равными энергиями. На диаграмме три p-орбитали каждого атома (всего шесть атомных орбиталей), объединяясь, порождают шесть молекулярных орбиталей. Атомные p_z-орбитали образуют σ-связывающую и σ-разрыхляющую МО, которые имеют энергии, отличные от энергий связывающих и разрыхляющих МО π_x и π_y, образованных атомными орбиталями p_x и p_y. Однако связывающие МО π_x и π_y имеют одинаковую энергию, и разрыхляющие МО π_x^* и π_y^* также обладают одинаковой энергией. Вырожденные пары π-МО изображены двумя близко расположенными линиями.

Фтор имеет девять электронов. Следовательно, у атома фтора два электрона находятся на 1s-орбитали, два электрона на 2s-орбитали и пять электронов на 2p-орбитали. Два атома F вместе обладают 18 электронами. Поэтому нужно разместить 18 электронов на соответствующих молекулярных орбиталях по тем же принципам, которые применялись при расселении электронов по атомным орбиталям при построении Периодической таблицы в главе 11 и при анализе молекулы водорода в главе 12. Как и раньше, мы будем следовать трём правилам заполнения МО. Во-первых, это принцип Паули, который утверждает, что на одной орбитали может находиться не более двух электронов и они должны иметь противоположные спины (противоположные спины изображаются стрелками вверх и вниз). Во-вторых, электроны размещаются сначала на самом низком энергетическом уровне, доступном без нарушения принципа Паули. В-третьих, это правило Хунда, согласно которому электроны по возможности не будут спаривать свои спины. В молекуле F₂ правило Хунда не влияет на результат размещения электронов по орбиталям. Но при рассмотрении молекулы кислорода O₂ оно будет играть важную роль.

На рис. 13.6 представлена диаграмма энергетических уровней молекулярных орбиталей для молекулы F₂ с электронами, корректно размещёнными по орбиталям. Энергетические уровни атомных орбиталей, показанные на рис. 13.5, здесь опущены, показаны только энергетические уровни МО. Первые два электрона занимают σ-связывающую МО, образованную 1s-орбиталями. Следующие два электрона заселяются на σ-разрыхляющую МО, образованную 1s-орбиталями. Электроны на связывающей МО имеют более низкую энергию, чем на атомных орбиталях отдельных атомов, а электроны на разрыхляющей МО имеют настолько же бо́льшую энергию. Поэтому данные четыре электрона не дают вклада в связывание молекулы F₂. Следующие четыре электрона занимают σ-связывающую и σ-разрыхляющую МО, образованные атомными 2s-орбиталями. И вновь они не дают вклада в связывание, поскольку имеется по два электрона на связывающей и разрыхляющей МО.

Рис. 13.6. Диаграмма энергетических уровней молекулярных орбиталей для двухатомной молекулы фтора F ₂ . Энергия атомных орбиталей не показана. Два атома фтора содержат 18 электронов. Они расселены по орбиталям в соответствии с правилами, которые обсуждались применительно к атомным орбиталям в главе 11. Связывающих МО на одну больше, чем разрыхляющих. Молекула F ₂ имеет одиночную связь

Далее в игру вступают p-электроны. Всего их десять — по пять от каждого атома F. Первые два занимают σ-связывающую МО, образованную атомными p_z-орбиталями. Затем четыре электрона заселяются на связывающие МО π_x и π_y. Четыре электрона могут разместиться на этих молекулярных орбиталях, поскольку имеется две МО и каждая в соответствии с принципом Паули может принять до двух электронов. Последние четыре электрона занимают разрыхляющие МО π_x и π_y. Эти четыре электрона на π-разрыхляющей МО компенсируют связывающее действие четырёх электронов на π-связывающих МО. Результирующий эффект соответствует действию одной пары связывающих электронов, которая остаётся нескомпенсированной, так что F₂ имеет связь порядка 1, как H₂. Говорят, что F₂ имеет одну связь, и это σ-связь. Единственная ковалентная связь возникает за счёт двух электронов на связывающей МО. Молекулярные орбитали — это волны амплитуды вероятности, которые распространяются на всю молекулу. Атомные ядра совместно используют эти электроны.

Молекулы неона не существует

Диаграмму энергетических уровней МО, представленную на рис. 13.6, можно использовать для рассмотрения гипотетической двухатомной молекулы неона Ne₂. В Периодической таблице неон занимает следующее место справа от фтора. На рис. 13.7 показан результат расселения 20 электронов от двух атомов неона по диаграмме энергетических уровней МО. Первые 18 электронов располагаются так же, как и в молекуле F₂. Однако есть ещё два электрона, и они должны занять разрыхляющую МО σ_z^*. Таким образом, для каждой пары электронов на связывающих МО имеется пара электронов на разрыхляющих МО. В результате связи не возникает. Молекулы Ne₂ не существует. Другие благородные газы также не образуют гомонуклеарных двухатомных молекул. На примере молекулы Ne₂ становится понятно, почему это так. Атом благородного газа имеет замкнутую оболочку. Два атома благородных газов имеют ровно столько электронов, сколько необходимо, чтобы заполнить все связывающие и разрыхляющие МО. Поэтому в совокупности связей не образуется.

Молекула кислорода: правило Хунда имеет значение

На одну позицию левее фтора в Периодической таблице находится кислород. Молекула O₂ является важным примером, на котором можно проиллюстрировать пару новых идей. На рис. 13.8 представлена диаграмма энергетических уровней МО, заполненная шестнадцатью электронами O₂, по восемь от каждого атома кислорода. Связывающие и разрыхляющие МО, образующиеся из 1s- и 2s-орбиталей, заполнены. Они не дают вклада в связывание. Имеется два электрона на связывающей МО σ_z^b и ни одного на соответствующей разрыхляющей МО. Кроме того, имеется четыре электрона на двух связывающих π-МО, но только два электрона на разрыхляющих π-МО. В результате возникают одна σ-связь и одна π-связь. Кислород имеет связь порядка 2, то есть двойную связь. Как будет показано далее, двойная связь сильнее и короче одиночной связи.

Рис. 13.7. Диаграмма энергетических уровней МО для гипотетической молекулы Ne ₂ . Два атома неона обладают двадцатью электронами. Получается одинаковое число связывающих и разрыхляющих электронов, так что связи не образуется. Молекулы Ne ₂ не существует

Молекула O₂ — это первый пример, в котором правило Хунда вступает в действие и играет важную роль. Обратите внимание: при заполнении энергетических уровней электронами два последних электрона имеют неспаренные спины. Возможность иметь неспаренные спины без нарушения принципа Паули появляется благодаря тому, что существует две разных разрыхляющих π-МО. Орбиталь π_x^* возникает за счёт бокового перекрытия двух атомных p_x-орбиталей (см. рис. 13.3), а орбиталь π_y^* появляется за счёт бокового перекрытия двух атомных p_y-орбиталей. Правило Хунда утверждает, что электроны будут занимать орбиталибез спаривания, если это не противоречит принципу Паули и не требует подъёма на значительно более высокоэнергетическую орбиталь. Две обсуждаемые разрыхляющие МО имеют одинаковую энергию, так что правило Хунда вступает в игру.

Рис. 13.8.Диаграмма энергетических уровней МО для молекулы O₂. Имеются одна пара σ-связывающих электронов и одна пара π-связывающих электронов. Молекула O₂ имеет двойную связь. Обратите внимание на неспаренные электроны связывающей π-МО

Электрон обладает магнитным моментом. В некотором смысле он действует как крохотный магнитный брусок. У него есть северный и южный полюса. Термин «спин»^{20} для квантового числа электрона пришёл из классической механики. В классической теории вращающийся пространственно распределённый заряд обладает магнитным моментом. Электрон — это волна амплитуды вероятности. Он имеет делокализованное распределение заряда. В результате у него есть магнитный момент, но этот факт не следует понимать как вращение в буквальном смысле. Это классическая идея. Дирак, которому мы обязаны концепцией абсолютного размера (см. главу 2), объединив квантовую теорию с теорией относительности Эйнштейна, показал, почему электрон обладает магнитным моментом. Электрон в действительности не вращается, но это название закрепилось. Магнитный момент электрона играет важную роль.

Когда спины двух электронов спарены, северный полюс одного крошечного магнита совпадает по направлению с южным полюсом другого. Магнитные свойства одного электрона компенсируют магнитные свойства другого. Однако в молекуле O₂ два электрона не спарены. Их спины имеют одинаковое направление. В результате молекула O₂ приобретает свойство, называемое парамагнетизмом. Она реагирует на магнит. Вода при температуре выше 100 °C находится в газообразном состоянии, но если охладить её до температуры ниже 100 °C, она превращается в жидкость. С кислородом происходит то же самое, но его требуется охлаждать гораздо сильнее. При комнатной температуре кислород является газом, но если очень сильно его охладить (ниже −183 °C), он переходит в жидкое состояние. Можно налить жидкий кислород в пробирку, подвешенную на нити. Если поднести к этой пробирке магнит, то он её притянет. Спины электронов (маленькие магнитные бруски) в молекулах O₂ выстраиваются вдоль магнитного поля внешнего макроскопического магнита. Эти выстроившиеся крошечные магнитики, складываясь вместе, придают жидкому кислороду магнитные свойства, и пробирка притягивается к внешнему магниту.

Корректное предсказание парамагнитных свойств O₂, сделанное на основе анализа диаграммы энергетических уровней МО, — это замечательный результат. Магнитный момент O₂ — это сугубо квантовый эффект, и наше предсказание того, что O₂ является парамагнетиком, появилось благодаря применению правила Хунда. Следуя определённым правилам, мы нарисовали линии, отвечающие энергетическим уровням. Затем, следуя другим правилам, мы разместили на этих линиях энергетических уровней стрелки, направленные вверх и вниз (расселили по ним электроны). На основе этих линий и стрелок мы смогли предсказать, что молекула кислорода является магнитной, хотя молекулы фтора и азота таковыми не являются.

Молекула азота

На рис. 13.9 представлена заполненная диаграмма энергетических уровней МО для азота N₂. Атом азота находится в Периодической таблице непосредственно слева от кислорода. Обратите внимание, что есть перестановка в порядке следования связывающих МО, порождённых p-электронами. Подробные квантовомеханические вычисления позволяют получить порядок следования и значения энергетических уровней МО. У азота этот порядок иной, чем у O₂ и F₂. Атом азота имеет семь электронов, так что молекула N₂ содержит 14 электронов. Как и в случае с F₂ и O₂, 1s- и 2s-электроны не участвуют в связывании, поскольку они заполняют как связывающие, так и разрыхляющие МО. На заполнение этих МО уходит восемь из 14 электронов. Остальные шесть электронов расселяются по трём связывающим МО — одной σ-МО и двум π-МО. На разрыхляющих π-МО и σ-МО, образованных p_z-орбиталями, электронов нет. Таким образом, N₂ имеет связь порядка 3, то есть тройную связь. Тройная связь сильнее и короче, чем двойная или одиночная. Обратите внимание, что в молекуле N₂ нет неспаренных электронов. Она не является парамагнитной. При низкой температуре (ниже −196 °C) азот становится жидким. Однако сдвинуть пробирку с жидким азотом с помощью магнита не получится, поскольку у него нет неспаренных спинов.

Одиночные, двойные и тройные связи

В главе 11, обсуждая связывание на основе положения атома в Периодической таблице, мы воспользовались представлением о том, что атом стремится сформировать ковалентные связи таким образом, чтобы совместное использование электронов позволяло ему достичь конфигурации благородного газа. Для обсуждаемых здесь элементов второй строки Периодической таблицы — азота, кислорода и фтора — таким благородным газом является неон. Как уже говорилось, атом фтора, который на один электрон отстаёт от конфигурации атома неона, будет совместно с другим атомом использовать один электрон. Атом кислорода, на два элемента отстающий от конфигурации атома неона, будет использовать два электрона, а атом азота, которому до неона не хватает трёх электронов, будет совместно использовать три электрона.

Рис. 13.9.Диаграмма энергетических уровней МО для молекулы N₂. Имеется одна дополнительная пара σ-связывающих электронов и две дополнительные пары π-связывающих электронов. N₂ имеет тройную связь

Здесь мы увидели, что F₂ образует одиночную связь, O₂ — двойную связь, а N₂ — тройную. Одиночный, двойной или тройной тип связи между атомами обозначают F−F, O=O и N≡N соответственно. О связи между атомами принято думать как о совместно используемых электронах. Ковалентная связь — это связь, образованная совместным использованием пары электронов. Двойная связь — это совместное использование двух пар электронов, тройная — трёх пар. Когда связывающие МО в точности компенсируются разрыхляющими МО, электроны в действительности не используются атомами совместно. Они находятся на молекулярных орбиталях, но связывающие МО порождают конструктивную интерференцию волн амплитуды вероятности, а разрыхляющие МО — деструктивную интерференцию и гасят друг друга. Электроны в этом случае называются неподелёнными парами. Эти пары электронов не дают вклада в связывание. Только одиночная связь, то есть совместно используемая пара электронов в молекуле F₂, обеспечивает каждому из атомов F дополнительный электрон, необходимый им для достижения конфигурации атома Ne. В молекуле O₂ двойная связь (совместное использование двух пар электронов) обеспечивает по два дополнительных электрона каждому атому O, что позволяет им достичь конфигурации атома Ne. В молекуле N₂ тройная связь (совместное использование трёх пар электронов) обеспечивает три дополнительных электрона каждому атому азота, наделяя их конфигурацией атома Ne.

В последовательности молекул F₂, O₂ и N₂ мы обнаружили одиночную, двойную и тройную связи. Совместное использование электронов даёт каждому атому конфигурацию как у атома Ne. Следующий элемент, находящийся слева от азота в Периодической таблице, — это углерод. Можно было бы предположить, что углерод будет формировать четверную связь, чтобы образовать молекулу C₂ и достичь конфигурации атома Ne. Однако C₂ не существует как стабильная молекула. Причину этого можно понять, если обратиться к рис. 13.9, где приведена диаграмма MO для N₂, и удалить два электрона с наибольшей энергией, то есть со связывающей МО σ_z^b. Это дало бы электронную конфигурацию молекулы C₂. Однако она имела бы не четверную, а двойную связь, образованную четырьмя электронами, находящимися на двух связывающих π-МО. Наличие только двух связей означает, что атомы углерода в молекуле C₂ получили бы за счёт совместного использования только по два, а не по четыре электрона, которые нужны каждому из них, чтобы достичь конфигурации атома Ne. Для достижения этой конфигурации углероду нужно образовать четыре связи, как, например, в молекуле CH₄. Он не может образовать четыре связи в молекуле C₂, и поэтому такой молекулы не существует^{21}.

Молекула F₂ имеет одиночную связь, O₂ — двойную связь, N₂ — тройную. Из табл. 13.1 видно, что порядок связи сильно влияет на её свойства. Чем больше порядок, тем меньше длина и выше энергия химической связи. Энергия связи — это та энергия, которую нужно передать в молекуле, чтобы разрушить связь. Разрушение связи означает разведение атомов на такое расстояние, на котором они перестают чувствовать друг друга. В следующей главе будет показано, что углерод может создавать одиночные, двойные и тройные связи с другим атомом углерода, если одновременно он образует связи с другими атомами, такими как атом водорода. Однако, прежде чем переходить к обсуждению молекул крупнее двухатомных, необходимо выйти за пределы гомонуклеарных двухатомных молекул и познакомиться с гетеронуклеарными двухатомными молекулами, чтобы понять, как молекулярные орбитали формируются неодинаковыми атомами.

Таблица 13.1. Влияние порядка связи на её свойства

Молекула: Порядок связи; Длина связи; Энергия связи

F₂: 1; 1,42Å; 2,6∙10⁻¹⁹Дж

O₂: 2; 1,21Å; 8,3∙10⁻¹⁹Дж

N₂: 3; 1,10Å; 15,6∙10⁻¹⁹Дж

Гетеронуклеарные двухатомные молекулы

В гомонуклеарных двухатомных молекулах МО образуются из атомных орбиталей с одинаковой энергией. В гетеронуклеарных двухатомных молекулах, например в молекуле фтороводорода (HF), два атома различаются. Поскольку атомы различны, энергия атомных орбиталей одного атома не совпадает с энергией атомных орбиталей другого. В молекуле HF атом водорода имеет один электрон на 1s-орбитали. Атом F имеет девять электронов на орбиталях 1s, 2s и 2p. Молекулы F₂ и H₂ имеют одиночные связи. На рис. 13.6 видно, что одиночная связь в F₂ — это σ-связь, возникшая за счёт связывающей МО σ_z^b. Эта связывающая МО формируется двумя атомными 2p_z-орбиталями, по одной у каждого атома F. Молекула H₂ имеет одну σ-связь за счёт связывающей МО, образованной двумя 1s-орбиталями (см. рис. 12.7). При образовании молекулы HF встаёт вопрос о том, какая орбиталь F будет объединяться с 1s-орбиталью H для получения МО, обеспечивающей связывание. Расчёты, проведённые в соответствии с квантовой теорией, показывают, что близкие по энергии состояния (атомные орбитали) могут объединяться и порождать МО с совместным использованием электронов. Атомные орбитали с сильно различающимися по энергии состояниями образуют МО, которые, по сути, эквивалентны атомным орбиталям и не дают вклада в связывание.

Энергия 1s-орбитали атома водорода равна −2,2∙10⁻¹⁸ Дж. (Напомним, знак «минус» означает, что электрон находится в связанном состоянии.) Энергия 1s-орбитали атома фтора (измеренная в молекуле F₂) составляет −1,1∙10⁻¹⁶ Дж. Таким образом, 1s-орбиталь атома F примерно в 50 раз ниже по энергии, чем 1s-орбиталь атома H. Это колоссальная разница в энергии, так что 1s-орбиталь водорода не будет образовывать МО с 1s-орбиталью фтора. Для сравнения: энергия 2p-орбитали фтора, которая составляет −2,8∙10⁻¹⁸ Дж, примерно на 25 % ниже энергии 1s-орбитали водорода, так что 2p-орбиталь фтора и 1s-орбиталь водорода достаточно близки по энергии, чтобы образовать полноценные МО.

У фтора имеются три 2p-орбитали: 2p_z, 2p_x и 2p_y. Чтобы решить, какая из них будет взаимодействовать с 1s-орбиталью водорода, надо определить, каким образом атомы будут сближаться друг с другом. Допустим, мы подносим атом H к атому F вдоль оси z, как показано в верхней части рис. 13.10. Две окружности в масштабе отражают относительные размеры атомов H и F. Лепестки 2p_y-орбитали фтора расположены перпендикулярно оси z, как показано в средней части рисунка. (Масштаб при изображении орбиталей не соблюдается.) Когда 2p_y-орбиталь перекрывается с водородной 1s-орбиталью, положительный лепесток 2p_y-орбитали будет интерферировать с 1s конструктивно, но отрицательный лепесток 2p_y-орбитали будет испытывать деструктивную интерференцию. Результат сведётся к тому, что в совокупности не будет ни неконструктивной, ни деструктивной интерференции. То же самое верно и в отношении 2p_x-орбитали. 2p_y- и 2p_x-орбитали не будут образовывать связывающих и разрыхляющих МО в молекуле HF.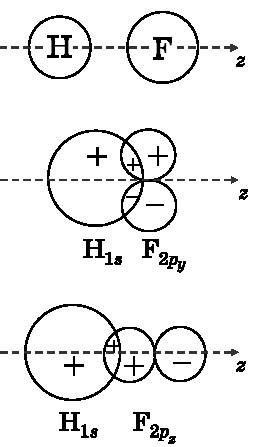

Рис. 13.10.Вверху: атомы H и F сближаются вдоль оси z. Окружности показывают относительные размеры атомов. В середине: перекрытие 1s-орбитали H и 2p_y-орбитали F. Возникает равная конструктивная (+) и деструктивная (−) интерференция в области перекрытия. МО не образуется. Внизу: перекрытие 1s-орбитали H и 2p_z-орбитали F. В области перекрытия возникает конструктивная интерференция

В нижней части рисунка показано, как положительный лепесток 2p_z-орбитали перекрывается с 1s-орбиталью, которую мы тоже будем считать положительной. Это перекрытие приводит к конструктивной интерференции волн амплитуды вероятности и может породить связывающую МО. Поскольку вдоль линии, соединяющей ядра, имеется ненулевая электронная плотность, эта связь является σ-связью. Если отрицательный лепесток 2p_z-орбитали атома F перекроется с положительной 1s-орбиталью атома H, то возникнет деструктивная интерференция, которая породит разрыхляющую МО.

Рис. 13.11.Диаграмма энергетических уровней молекулярных орбиталей для HF. Атомные орбитали валентных электронов показаны слева и справа. Атомная 2p_z-орбиталь F объединяется с атомной 1s-орбиталью H и даёт связывающую ( σ^b) и разрыхляющую ( σ^*) МО. σ^b заполнена одним электроном атома H и одним электроном атома F; σ^* не заполнена. В целом возникает одна связь. Другие электроны атома F не дают вклада в связывание. Это неподелённые пары электронов

Как говорилось выше, энергия 1s-орбитали фтора настолько меньше, чем у 1s-орбитали водорода, что 1s-электроны фтора не принимают участия в связывании. Вклад в связывание атомов дают самые внешние электроны, то есть находящиеся на его последней заполненной оболочке. Это валентные электроны. Для элементов второй строки Периодической таблицы, таких как фтор, валентными являются 2s- и 2p-электроны. Обычно на диаграммах энергетических уровней молекулярных орбиталей изображаются только орбитали, относящиеся к валентным электронам, поскольку именно эти орбитали могут участвовать в связывании. На рис. 13.11 приведена диаграмма энергетических уровней молекулы HF, причём на ней опущены 1s-орбиталь атома F и находящиеся на ней электроны. Масштаб при изображении интервалов между энергетическими уровнями не соблюдается. Как уже отмечалось в связи с рис. 13.10, 1s-орбиталь атома H будет объединяться с 2p_z-орбиталью атома F, образуя связывающую (σ^b) и разрыхляющую (σ^*) МО. Это показано на диаграмме пунктирными линиями. Данная диаграмма похожа на диаграмму энергетических уровней, приведённую на рис. 13.5, за исключением того, что теперь атомные орбитали, формирующие МО, имеют неодинаковые энергии.

Фтор имеет девять электронов. Два из них находятся на 1s-орбитали, остаётся семь. Водород имеет один электрон. Таким образом, имеется восемь валентных электронов, которые надо расселить по энергетическим уровням МО. Первые два отправляются на уровень, обозначенный 2s. Энергия 2s-орбитали атома фтора намного меньше, чем энергия 1s-орбитали атома водорода, и эти электроны не участвует в образовании связи. Поэтому молекулярная 2s-орбиталь — это, по сути, то же самое, что атомная 2s-орбиталь фтора. Два электрона на этой 2s-орбитали образуют неподелённую пару. Следующие два электрона заселяются на σ^b-связывающую МО. Последние четыре электрона занимают орбитали 2p_x и 2p_y. И вновь это фактически атомные орбитали фтора. Они не играют роли в связывании. Эти четыре электрона образуют ещё две неподелённые пары. Хотя неподелённые пары не участвуют в связывании, они влияют на форму многоатомных молекул, что будет обсуждаться в главе 14.

Итоговый результат состоит в том, что имеется два электрона на связывающей МО и нет ни одного электрона на разрыхляющей МО. Таким образом, молекула HF имеет одиночную связь. Водород и фтор делят между собой пару электронов на связывающей МО. Водороду это совместное использование даёт дополнительный электрон, необходимый для того, чтобы достичь электронной конфигурации инертного газа гелия. Фтору совместное использование даёт дополнительный электрон, необходимый для достижения электронной конфигурации благородного газа неона.

Визуальные модели молекул

Молекула HF, подобно молекулам F₂, O₂ и N₂, является двухатомной и потому линейной молекулой. В следующей главе мы будем говорить о молекулах более сложной формы. Есть целый ряд способов изобразить строение молекулы. Формулу молекулы HF можно записать в виде H−F, обозначив таким образом, что в ней имеет место одиночная связь. В более сложных молекулах такой способ представления может показывать, какие атомы с какими связаны и какого порядка связью. Однако этот способ не позволяет продемонстрировать трёхмерную геометрию и дать представление о том, как в действительности выглядит молекула.

Надо отметить, что уподобление молекулы какому-либо предмету фундаментально некорректно. Молекула HF — это два ядра, окружённых волнами амплитуды вероятности, которые являются электронами. Тем не менее существуют представления, полезные для обсуждения природы молекул. На рис. 13.12 показаны два таких представления молекулы HF. Вверху представлена шаростержневая модель молекулы^{22}. Она отражает связь между атомами и их относительные размеры. Атом H изображён светлым тоном, а атом F — тёмным. Связь между атомами преувеличенно длинная. Внизу изображена объёмная модель^{23}. Бо́льшая часть электронной плотности сосредоточена внутри перекрывающихся сфер. Здесь верно передаются относительные размеры атомов и межъядерные расстояния. Тон и чёткие линии между атомами служат для большей наглядности. В действительности разделения электронов между атомами нет.

Материал этой и следующей глав необходим для понимания связей в многоатомных молекулах. В следующей главе нам понадобится расширить изложенные здесь идеи на молекулы, содержащие более двух атомов. Многоатомные молекулы могут иметь разные формы, и для их понимания мы введём новое понятие гибридных атомных орбиталей. В последующих главах материал глав 13 и 14 будет использоваться для анализа широкого круга вопросов, например для выяснения, что такое ненасыщенные жиры и чем они отличаются от других жиров.

Рис. 13.12. Различные представления молекулы HF. H — светлый тон; F — тёмный. Вверху: шаростержневая модель показывает, как связаны атомы, а также их относительные размеры. Внизу: объёмная модель, которая более реалистична

14. Более крупные молекулы: формы многоатомных молекул

Окружающий нас мир состоит из многоатомных молекул. Так называют молекулы, состоящие из более чем двух атомов. По размерам они варьируются от трёхатомных молекул, таких как углекислота (CO₂), которая является важнейшим парниковым газом, до молекул, состоящих из тысяч атомов, таких как крупные протеины, ответственные за большинство биологических функций. Как говорилось в главе 12, двухатомные молекулы могут иметь только одну форму — линейную. Более крупные молекулы, однако, могут быть очень сложными по форме и строению. Например, насыщенные жиры, ненасыщенные жиры и полиненасыщенные жиры различаются формой и строением, которые определяются природой химических связей. Конкретная большая молекула может иметь более одной формы. Транс-жиры, которые сегодня частично удаляются из пищи (см. главу 16), отличаются лишь формой от молекул, состоящих из той же последовательности атомов, но не являющихся транс-жирами. Центральный вопрос при изучении молекул состоит в том, каким образом они приобретают форму и как различные возможные формы молекул образуются из одних и тех же атомов, соединённых между собой одним и тем же способом.

Прежде чем двигаться дальше, надо подчеркнуть, что ковалентная связь, ответственная за удержание атомов в молекулах, представляет собой сугубо квантовомеханическое явление. Объяснить природу химических связей и строение молекул до появления квантовой теории было невозможно. Лайнус Полинг (1901–1994) получил Нобелевскую премию по химии в 1954 году

«за результаты исследования природы химической связи и их применение к объяснению строения сложных молекул».

Достойно упоминания, что Лайнус Полинг был одним из немногих людей, заслуживших две Нобелевские премии. В 1962 году он получил Нобелевскую премию мира.

Формы молекул: тетраэдрический метан

Для изучения форм молекул и того, каким образом они определяются химическими связями, нам необходимо познакомиться с некоторыми новыми представлениями об атомных орбиталях. Чтобы коснуться этих важных вопросов, мы воспользуемся метаном в качестве примера относительно простой многоатомной молекулы.

Метан (природный газ) имеет формулу CH₄. Теперь обратимся вновь к Периодической таблице и положению в ней углерода (см. рис. 11.4). Заметьте, что углероду необходимо создать четыре ковалентные связи за счёт совместно используемых пар электронов, чтобы достичь такой замкнутой конфигурации оболочки, как у неона. В метане углерод создаёт четыре связи с четырьмя атомами водорода. Схему взаимосвязи атомов можно изобразить в виде простой диаграммы, представленной в левой части рис. 14.1. Каждая линия соответствует ковалентной связи, образованной электронной парой. Однако эта диаграмма мало что говорит нам о форме молекулы метана, которая не является плоской. В правой части рисунка изображена шаростержневая модель, которая отражает трёхмерную форму молекулы метана. (Шаростержневые и объёмные модели молекул обсуждались в конце главы 13.)

Метан представляет собой правильный тетраэдр. Представьте, что у вас есть модель, изображённая справа на рис. 14.1, и вы склеиваете куски бумаги в форме правильных треугольников, как раз закрывающих три атома водорода. Можно склеить между собой четыре таких треугольника — три по бокам и один в основании. Эти четыре треугольника образуют правильную треугольную пирамиду с атомами водорода в вершинах и углеродом в центре. Углы, образуемые прямыми, идущими от двух атомов водорода к углероду, составляют ровно 109,5°^{24}. Это верно для всех четырёх таких углов. Они равны между собой. В идеальной тетраэдрической молекуле этот угол составляет 109,5°.

Рис. 14.1. Слева: диаграмма, показывающая связи в молекуле метана, но не отражающая её трёхмерную форму. Справа: трёхмерная шаростержневая модель, которая демонстрирует тетраэдрическую форму его молекулы

Форма определяется минимизацией отталкивания между связями

Почему метан имеет тетраэдрическую форму? В главе 13 мы узнали, что связывающие молекулярные орбитали концентрируют электронную плотность между атомными ядрами. Концентрация электронной плотности между ядрами показана на рис. 13.2 и 13.3 для σ- и π-связей. В главе 13 обсуждались двухатомные молекулы, в которых связываются только два атома. Мы не беспокоились о том, как будет организовываться множество атомов с определённым набором связей между ними. Хотя для детального расчёта форм молекул необходима квантовая теория, фундаментальные причины, по которым та или иная молекула имеет определённую форму, например тетраэдрическую, очень просты. В многоатомных молекулах электроны, совместно используемые двумя атомами для образования связи, концентрируют электронную плотность между ядрами точно так же, как это происходит в двухатомных молекулах. Однако в многоатомных молекулах имеется множество связей, каждая из которых даёт высокую плотность отрицательно заряженных электронов. Отрицательно заряженные области — связи — отталкиваются друг от друга. Попросту говоря, связи стремятся располагаться как можно дальше друг от друга. Образование связей снижает энергию системы относительно разделённых атомов. Если энергия не снижается, связи не формируются. Но для достижения наименьшей возможной энергии система атомов принимает конфигурацию, которая минимизирует электронное отталкивание за счёт того, что связи располагаются дальше друг от друга.

В молекуле метана тетраэдрическая форма минимизирует отталкивание между связями. Посмотрите на схему, представленную на рис. 14.1 слева. Четыре атома водорода расположены в одной плоскости. Если мы удерживаем их в этой плоскости, они максимально удалены друг от друга. Угол между двумя соседними связями составляет 90°. Если для атомов, располагающихся в этой плоскости, мы увеличим один из углов и сделаем его больше 90°, чтобы ещё сильнее раздвинуть две из водород-углеродных связей, эти связи приблизятся к двум другим связям. Таким образом, если четыре атома водорода удерживаются в одной плоскости с атомом углерода, лучшее, чего можно достичь, — это угол 90° между связями.

Однако нет никаких причин, по которым все атомы должны лежать в одной плоскости. В структуре, изображённой на рис. 14.1 слева, угол между верхним и нижним атомами H равен 180°, и эти две C−H-связи находятся далеко друг от друга; то же самое верно и для атомов H, находящихся слева и справа. Представьте теперь, что верхний и нижний атомы H выталкиваются выше плоскости страницы, а правый и левый атомы H — ниже плоскости страницы при сохранении длины связей. Верхняя и нижняя C−H-связи сближаются друг с другом, и угол между ними становится меньше 180°, но они удаляются от правой и левой C−H-связей. Подъём верхней и нижней C−H-связей над плоскостью страницы и опускание левой и правой C−H-связей ниже, под эту плоскость, уменьшают совокупное взаимодействие между связями. Взаимодействие между верхней и нижней связями усиливается, но исходно они были очень далеки друг от друга. Это также верно для левой и правой связей. Однако если углы между верхней и нижней или левой и правой связями уменьшатся слишком сильно, отталкивание снова начнёт увеличиваться. Имеется наилучший угол, и он составляет 109,5°, что соответствует правильному тетраэдру. При таком угле электроны C−H-связей удерживаются так далеко друг от друга, насколько это возможно.

Неподелённые пары тоже имеют значение

В главе 11 мы узнали, что для получения замкнутой электронной конфигурации атом C нуждается в образовании четырёх связей, для атома N требуется три связи, а для атома O — две связи. Если это будут связи с водородом, то получится метан, аммиак и вода: CH₄, NH₃ и H₂O. При обсуждении молекулы HF в конце главы 13 мы отметили, что некоторые электроны атома F совершенно не были вовлечены в образование связей. Эти электроны находятся в спаренном состоянии, по сути, на атомных орбиталях, и называются неподелёнными парами. Неподелённые пары — это пары несвязывающих электронов, которые вызывают повышение электронной плотности в той области пространства, которую они занимают. Электроны, образующие связи, избегают располагаться вблизи неподелённых пар. Поэтому хотя неподелённые пары не являются связями, они также влияют на форму молекул. В связях электроны используются совместно и в основном концентрируются где-то между двумя атомами. Неподелённые пары не тянутся ко второму атому. Как следствие, их электронные облака расположены вблизи атомов, которым они принадлежат, и по размерам они больше, чем облака пар, образующих связи.

На рис. 14.2 изображены модели молекул метана, аммиака и воды. У аммиака имеется одна неподелённая пара, а у воды — две. Если принять в расчёт неподелённые пары, то все три молекулы имеют в своей основе тетраэдрическую форму. Однако аммиак и вода представляют собой неправильные тетраэдры. Неподелённая пара аммиака больше по размеру, чем связывающие пары. Чтобы минимизировать общее электрон-электронное отталкивание и достичь наименьшей энергии, связи удаляются от неподелённых пар, а значит, сближаются между собой. Угол HNH в молекуле аммиака составляет 107,3° — чуть меньше, чем в правильном тетраэдре. У воды две неподелённые пары, и поэтому угол между водород-кислородными связями уменьшается ещё сильнее — до 104,5°.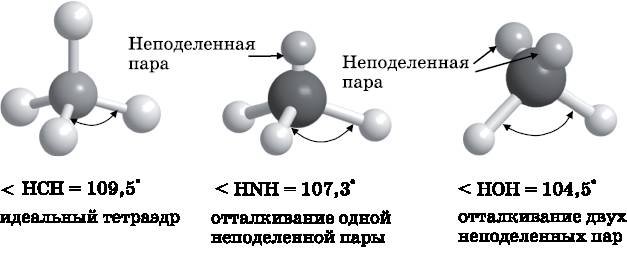

Рис. 14.2. Метан (слева), аммиак (посередине) и вода (справа). Неподелённые пары электронов отталкивают связывающие пары электронов, заставляя связи сближаться, из-за чего уменьшаются углы между связями атомов H с центральным атомом

Молекулы треугольной формы

Если центральный атом связан только с тремя другими атомами, молекула будет иметь прямоугольную форму с четырьмя атомами, лежащими в одной плоскости. На рис. 14.3 изображены две треугольные молекулы: BH₃ и H₂CO (формальдегид). Молекула BH₃ существует, но она химически очень активна, поскольку ей не хватает двух электронов до замкнутой конфигурации оболочки, как у неона. В BH₃ каждый атом H имеет одиночную связь с B. Угол HBH равен в точности 120°. Атомы водорода образуют идеальный равносторонний треугольник. При такой форме молекулы связи оказываются максимально удалёнными друг от друга, что снижает энергию за счёт уменьшения отталкивания между связывающими электронами каждой связи.

В главе 13 на диаграмме МО для O₂ (см. рис. 13.8) показано, что молекула кислорода имеет двойную связь. В формальдегиде (пахучей жидкости, которой заполняют банки с биологическими образцами в кабинетах биологии) атом O имеет двойную связь с атомом C. Эта двойная связь показана на шаростержневой модели двумя цилиндрами, соединяющими атомы, вместо одного. Двойная связь обеспечивает атому O замкнутую неоновую конфигурацию оболочки, как в молекуле О₂. Атом C нуждается в двух дополнительных электронах, чтобы получить замкнутую неоновую конфигурацию оболочки, и он получает их за счёт одиночных связей с двумя атомами H. Мы ещё обсудим подробно двойные связи, чтобы разобраться, как они могут образовываться из атомных орбиталей, но сейчас нам нужно лишь понять, что двойная связь концентрирует две пары электронов между атомами C и O. Из-за этой дополнительной электронной плотности двойная связь становится шире одиночной. Более толстая двойная связь C=O расталкивает одиночные связи C−H, заставляя их сближаться друг с другом. Все углы обозначены на рис. 14.3. В результате молекула формальдегида, оставаясь плоской треугольной, отклоняется от формы равностороннего треугольника.

Рис. 14.3. Слева: молекула BH ₃ . Атомы лежат в одной плоскости. Связи HB являются одинарными, атомы водорода образуют равносторонний треугольник. Все углы HBH равны 120°. Справа: молекула H ₂ CO (формальдегид). Атомы лежат в одной плоскости. Связь CO — двойная. Углы не равны

Переходящие электроны

Возвращаясь к метану, зададимся вопросом: каким образом он формирует четыре связи в тетраэдрической конфигурации? В главе 11 обсуждались электронные конфигурации атомов (см. рис. 11.1). Углерод имеет шесть электронов: два на 1s-орбитали, два на 2s-орбитали и два на 2p-орбитали. Валентные электроны, то есть участвующие в образовании химических связей, — это 2s- и 2p-электроны. В верхней части рис. 14.4 показаны энергетические уровни атомных орбиталей с заполняющими их четырьмя валентными электронами. 1s-электроны не показаны.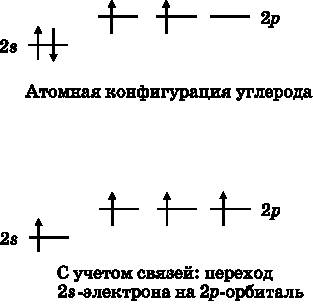

Рис. 14.4. Вверху: атомные валентные орбитали электрона с четырьмя валентными электронами. Внизу: при образовании химических связей атом углерода «повышает» 2s-электрон до уровня 2p, чтобы получить четыре неспаренных электрона для образования четырёх связей с другими атомами

Как отмечалось в главе 11 и ранее в этой главе, углерод образует четыре связи. В метане он создаёт четыре электронные пары, совместно используемые с четырьмя атомами водорода. Каждый атом H вкладывает один электрон. Поэтому углерод должен иметь четыре неспаренных электрона для образования этих связей. Каждый неспаренный электрон углерода может объединиться с одним электроном водорода и образовать связывающую пару электронов. Чтобы иметь четыре неспаренных электрона, углерод «поднимает» 2s-электрон на 2p-орбиталь, как это показано в нижней части рис. 14.4. У изолированного атома углерода такая конфигурация не возникает, если только не передать ему значительное количество энергии. Для атома углерода перемещение 2s-электрона на 2p-орбиталь — это переход к конфигурации с повышенной энергией. Однако в случае, когда атомы образуют молекулы, электроны и ядра различных атомов влияют друг на друга. Представьте себе четыре атома H, приближающихся к атому C. Теперь система стремится перейти в низшее энергетическое состояние для всех пяти атомов. Образование четырёх связей уменьшает эту энергию сильнее, чем её повышает переход 2s-электрона на 2p-орбиталь.

Гибридные атомные орбитали: линейные молекулы

Итак, мы разобрались, каким образом углерод образует четыре связи, необходимые для молекулы метана. Но почему она имеет тетраэдрическую форму? Три 2p-орбитали — это p_x, p_y и p_z. Эти три орбитали перпендикулярны друг другу, то есть для любой их пары угол между ними составляет 90°. Если бы три атома H были связаны с 2p-орбиталями, то угол между связями должен был составлять 90°. Далее, 2s-орбиталь сферическая. 1s-орбиталь четвёртого атома H должна была бы объединиться с углеродной 2s-орбиталью. Если бы больше ничего не происходило, то ясно, что использование 2s-орбитали и трёх 2p-орбиталей углерода не привело бы к появлению у метана четырёх совершенно идентичных C−H-связей в тетраэдрической конфигурации. Кроме того, каким образом углерод образует треугольную молекулу формальдегида или линейную молекулу углекислого газа O=C=O? Во всех этих конфигурациях — тетраэдрической, треугольной и линейной — углеродные связи задействуют всё те же 2s- и 2p-орбитали.

В формальдегиде и углекислом газе имеются двойные связи, которых мы вскоре коснёмся. Чтобы разобраться в важных свойствах атомных орбиталей, которые могут придавать молекулам линейную, треугольную или тетраэдрическую форму, мы рассмотрим химические связи в гидриде бериллия BeH₂, бора́не BH₃ и метане CH₄. Бериллий и бор в молекулах BeH₂ и BH₃ не имеют замкнутой оболочки, как у инертного газа неона, поэтому они химически очень активны. Создать эти молекулы можно, но они будут реагировать буквально со всем, с чем вступают в контакт, образуя новые молекулы, в которых Be и B имеют замкнутые конфигурации оболочек. Здесь мы рассматриваем их лишь как удобные примеры.

Бериллий имеет два электрона сверх замкнутой электронной конфигурации гелия. У отдельного атома эти два электрона спарены на 2s-орбитали. Они являются валентными электронами бериллия. В молекуле BeH₂ каждый атом H имеет по одному электрону на 1s-орбитали. Чтобы бериллий образовал две пары электронных связей, по одной для каждого атома H, он должен поднять один из 2s-электронов на 2p-орбиталь, которую мы примем за 2p_z, как показано в верхней части рис. 14.5.

Рис. 14.5. Вверху: валентные электроны Be, один из которых перешёл на 2p _z -орбиталь. Ниже: 2s- и 2p _z -орбитали Be, показанные по отдельности. Ниже: сумма 2s- и 2p _z -орбиталей даёт гибридную атомную орбиталь sp _z+ . Ниже: разность 2s и 2p _z -орбиталей даёт гибридную орбиталь sp _z− . Внизу: две гибридные орбитали бериллия направлены в противоположные стороны вдоль оси z

Ниже на этом рисунке 2s- и 2p_z-орбитали схематически показаны по отдельности. В действительности они имеют общий центр, совпадающий с ядром Be. Эти орбитали являются волнами амплитуды вероятности электрона. Волны могут складываться и вычитаться, порождая новые волны. Начнём с двух атомных орбиталей — 2s и 2p_z; далее путём сложения и вычитания получим две новые атомные орбитали, называемые гибридными орбиталями. Когда волны складываются, получаются области конструктивной и деструктивной интерференции, поскольку лепестки волн амплитуды вероятности имеют знак. На третьем сверху изображении на рис. 14.5 показана сумма 2s- и 2p_z-орбиталей. Она называется sp-гибридизированной орбиталью и обозначается sp_z+, поскольку является гибридом, полученным из s-орбитали и 2p_z-орбитали, а её большой положительный лепесток направлен в положительную сторону оси z.

На втором снизу изображении на рис. 14.5 показана разность 2s- и 2p_z-орбиталей. Один из способов представить себе это состоит в том, чтобы просто отразить 2p_z-орбиталь с верхнего изображения, так чтобы её положительный лепесток смотрел влево, а не вправо, и после этого выполнить сложение. Мы обозначили эту гибридную орбиталь sp_z−, поскольку её большой положительный лепесток направлен в отрицательную сторону оси z. Эта орбиталь имеет такую же форму, как sp_z+, но ориентирована в противоположную сторону. На нижнем рисунке схематически изображены гибридные атомные орбитали в том виде, в каком они присутствуют в атоме Be. Имеется одно ядро бериллия с двумя гибридными орбиталями, ориентированными по направлениям +z и −z соответственно.

Образуя молекулу BeH₂, бериллий будет использовать две гибридные атомные орбитали для формирования электронных пар на молекулярных орбиталях, связывающих его с двумя атомами водорода. Эти связи схематически изображены на рис. 14.6. В верхней части рисунка показаны два атома водорода: H_a и H_b, приближающиеся к атому Be. Электроны атомов водорода находятся на 1s-орбиталях 1s_a и 1s_b. У бериллия имеются две гибридные атомные орбитали: sp_z− и sp_z+, направленные в сторону 1s-орбиталей водорода. В средней части рисунка схематически показано перекрытие атомных орбиталей. Водородная 1s_a-орбиталь слева образует связывающую МО с гибридной атомной орбиталью sp_z− бериллия. Это связывающая МО будет содержать два электрона: один от водорода и один из двух валентных электронов бериллия. Водородная 1s_b-орбиталь справа образует связывающую МО с гибридной атомной орбиталью sp_z+. Электрон атома H_b и другой валентный электрон атома Be образуют ещё одну ковалентную связь. Это будут σ-связи, поскольку электронная плотность вдоль линии, соединяющей ядра, отлична от нуля. В результате получается линейная молекула BeH₂, изображённая в нижней части рисунка.

Рис. 14.6. Вверху: два атома H приближаются к атому Be. В середине: 1s-орбитали атома H образуют парные электронные связи с двумя sp-гибридизированными орбиталями атома Be, в результате чего формируется линейная молекула BeH ₂ , изображённая внизу в виде шаростержневой модели

Молекула BeH₂ имеет шесть электронов: две пары связывающих электронов и два электрона на 1s-орбитали атома Be. Важно отметить, что все эти электроны являются волнами амплитуды вероятности, которые охватывают всю молекулу. Когда говорится, что 1s_a-электрон создаёт связывающую электронную пару с sp_z−-электроном, — это «бухгалтерская» условность. Все электроны свободно перемещаются по целой молекуле. Однако распределения вероятности для электронов таковы, что в любой данный момент электронная плотность, связанная с атомом Be и одним из атомов H, соответствует одной связи, а электронная плотность, связанная с атомом Be и другим атомом H, соответствует другой связи.

Гибридные атомные орбитали: треугольные молекулы

Как отмечалось при обсуждении рис. 14.3, молекула BH₃ треугольная с углами 120° между связями. Атом бора имеет три валентных электрона: два на 2s-орбитали и один на 2p-орбитали. Для образования трёх электронных пар, совместно используемых с тремя атомами водорода, атому бора требуется три неспаренных электрона. В верхней части рис. 14.7 показано, что атом B поднимает один электрон с 2s-орбитали на 2p-орбиталь, чтобы получить три неспаренных электрона. Если молекула лежит в плоскости xy, то задействованными в образовании связей 2p-орбиталями будут 2p_x и 2p_y. Для того чтобы молекула BH₃ имела форму равностороннего треугольника, триатомные орбитали бора гибридизируются и дают три гибридные атомные орбитали: sp_a², sp_b² и sp_c². Обозначение sp² указывает на то, что гибридные орбитали состоят из одной s-орбитали и двух разных p-орбиталей. Мы начинаем с трёх разных орбиталей: 2s, 2p_x и 2p_y. Орбитали никогда не возникают и не пропадают, поэтому получаются три различные гибридные орбитали. Они показаны в средней части рис. 14.7. Каждая орбиталь имеет положительный и отрицательный лепестки. Соседние лепестки расположены под углом 120° по отношению друг к другу. Каждая из орбиталей содержит по одному из трёх неспаренных валентных электронов атома бора.

В нижней части рис. 14.7 показано связывание атома B с тремя атомами H. Каждый атом H имеет единственный 1s-электрон. 1s-орбиталь атома H объединяется с sp²-орбиталью атома B и образует связывающую молекулярную орбиталь. В результате появляются связывающие пары электронов. Каждая из этих связей между атомами B и H является σ-связью, поскольку имеется ненулевая электронная плотность на прямой, соединяющей ядра. Модель молекулы BH₃ представлена на рис. 14.3.

Рис. 14.7.Вверху: валентные электроны бора, один из которых поднят на 2p — орбиталь. Посередине: 2s-, 2p_x- и 2p_y-орбитали бора объединяются тремя способами и образуют три гибридные атомные орбитали: sp_a², sp_b²и sp_c². Угол между лепестками составляет 120°. Внизу: три гибридные орбитали атома бора образуют связи с 1s-орбиталями трёх атомов H

Гибридные атомные орбитали: тетраэдрические молекулы

В молекуле метана углерод создаёт четыре связи с четырьмя атомами водорода. Как говорилось выше и показано на рис. 14.1 и 14.2, молекула метана имеет форму тетраэдра. На рис. 14.4 видно, что для создания четырёх валентных связей, совместно использующих электронные пары, углерод поднимает один из своих 2s-электронов на 2p-орбиталь. В результате у него появляется четыре неспаренных электрона на 2s-, 2p_x-, 2p_y- и 2p_z-орбиталях. При обсуждении рис. 14.4 уже довольно подробно объяснялось, что эти четыре атомные орбитали не могут породить одинаковые связи с четырьмя атомами водорода и привести к появлению тетраэдрической молекулы. Поэтому 2s-, 2p_x-, 2p_y- и 2p_z-орбитали объединяются в четырёх различных комбинациях и образуют четыре гибридные атомные орбитали: sp_a³, sp_b³, sp_c³ и sp_d³. Обозначение sp³ указывает на то, что каждая из четырёх гибридных атомных орбиталей является комбинацией s-орбитали и трёх различных p-орбиталей.

На рис. 14.8 показано, что четыре sp³-орбитали перекрываются с четырьмя 1s-орбиталями атомов водорода. Изображены только положительные лепестки sp³-орбиталей. Каждая из них имеет небольшой отрицательный лепесток, направленный в сторону, противоположную положительному лепестку, аналогично тому, как это показано на среднем изображении рис. 14.7 для sp²-орбиталей. Орбитали, изображённые штриховыми кривыми, лежат в плоскости страницы. Орбиталь, показанная сплошной кривой, выступает под углом над плоскостью страницы, а орбиталь, показанная штрихпунктирной линией, уходит под углом за плоскость страницы. Угол между любой парой sp³-лепестков составляет 109,5°, что обеспечивает правильную тетраэдрическую форму, о которой говорилось при обсуждении рис. 14.1 и 14.2.

На рис. 14.2 изображены молекулы метана, аммиака и воды. Как уже говорилось, все они имеют тетраэдрическую форму, если включить в рассмотрение неподелённые пары, но молекулы аммиака и воды имеют форму не совсем правильных тетраэдров. Подобно метану, аммиак и вода также используют sp³-гибридизацию для образования связей. Азот в аммиаке NH₃ имеет пять валентных электронов. Два из них образуют неподелённую пару. Она не участвует в образовании химических связей. Азот использует три из своих четырёх гибридных sp³-орбиталей для соединения с тремя атомами H. Четвёртая sp³-орбиталь содержит неподелённую пару.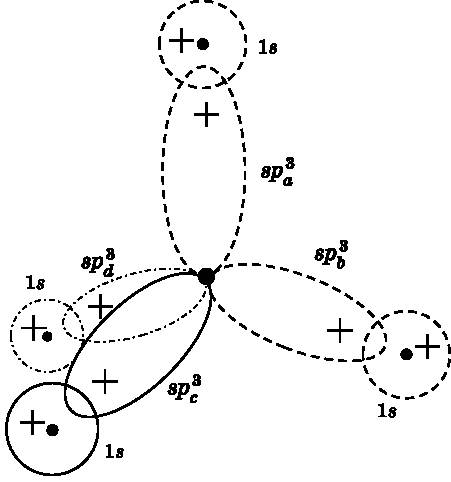

Рис. 14.8. Четыре sp ³ -гибридизированные атомные орбитали углерода и четыре 1s-орбитали водорода в молекуле метана, где атом углерода соединён с четырьмя атомами водорода. Штриховые орбитали лежат в плоскости страницы. Сплошная орбиталь выступает над этой плоскостью. Штрихпунктирная орбиталь лежит за плоскостью страницы. Показаны только положительные лепестки гибридных sp ³ -орбиталей. Четыре гибридные sp ³ -орбитали образуют правильный тетраэдр

Как уже говорилось, угол, образуемый связями H−N−H, немного меньше угла в правильном тетраэдре (109,5°), поскольку пространственное распределение неподелённой пары электронов несколько шире, чем у связывающей пары электронов N−H, и эта более широкая неподелённая пара подталкивает N−H-связи немного ближе друг к другу. Кислород в молекуле воды H₂O имеет шесть валентных электронов. Четыре из них образуют две неподелённые пары, которые не участвуют в химической связи. Кислород использует две свои гибридные sp³-орбитали для образования связей с двумя атомами водорода. Две другие sp³-орбитали заняты неподелёнными парами. Эти две неподелённые пары приводят к тому, что угол HOH оказывается меньше, чем угол в правильном тетраэдре, равный 109,5°(см. 14.2).

Углеводороды с одиночной связью

Углеводороды — это молекулы, целиком состоящие из атомов углерода и водорода. Мы начнём обсуждение более сложных, чем метан, углеводородов с молекул, имеющих лишь одиночные связи. Следующим по простоте углеводородом после метана является этан. Он содержит два атома углерода и шесть атомов водорода, а его химическая формула — C₂H₆. На рис. 14.9 строение этана представлено тремя способами. Вверху показаны только связи между атомами. Каждый атом углерода имеет одиночные связи с тремя атомами водорода и одиночную связь с другим углеродом. В средней части рисунка показаны гибридные атомные орбитали, обеспечивающие химическую связь. Для создания четырёх связей, совместно использующих электронные пары, каждый атом углерода задействует четыре гибридные sp³-орбитали — так же, как и в метане. Три из этих орбиталей у каждого атома углерода служат для создания связи с тремя атомами водорода. Эти sp³-орбитали объединяются с водородными 1s-орбиталями, образуя связывающие МО, обеспечивающие σ-связи. Четвёртая sp³-орбиталь каждого атома углерода образует МО с sp³-орбиталью другого углерода и порождает углерод-углеродную σ-связывающую МО.

В нижней части рис. 14.9 представлено стандартное схематическое изображение пространственного расположения атомов в молекуле. Атомы, которые связаны и лежат в плоскости страницы, соединяются сплошными линиями. Связанные атомы, которые выступают над плоскостью страницы, соединяются узкими закрашенными треугольниками, острый конец которых направлен на атом в плоскости страницы, а противолежащее ему основание располагается возле атома, выступающего над плоскостью. Связанные атомы, которые лежат за плоскостью страницы, соединяются незакрашенными треугольниками, основание которых прилегает к атому в плоскости страницы, а острый угол указывает на атом, находящийся за этой плоскостью. Из представленного схематического изображения видно, что оба атома углерода находятся в центрах тетраэдров. Между любой парой связей атома углерода имеется характерный для тетраэдра угол, равный 109,5°. Длина C−H-связи составляет 1,07 Å (1,07∙10⁻¹⁰ м), а длина связи C−C — 1,54 Å. Атомы углерода крупнее атомов водорода, поэтому расстояние между центрами двух атомов углерода больше, чем в случае атомов C и H.

Рис. 14.9.Три схемы молекулы этана C₂H₆. Вверху: связи между атомами. В середине: каждый атом углерода имеет четыре sp³-гибридизированные атомные орбитали, три из которых связывают с атомами водорода, а четвёртая — с другим атомом углерода. Сплошные кривые лежат в плоскости страницы, штриховые — над плоскостью страницы, пунктирные — за плоскостью страницы. Внизу: пространственное строение молекулы. Линии лежат в плоскости страницы; закрашенные треугольники поднимаются над плоскостью страницы; незакрашенные треугольники уходят за плоскость страницы. Конфигурация связей обоих атомов углерода тетраэдрическая с углом между связями 109,5°. Связь C−C длиннее связей C−H

На рис. 14.10 представлены шаростержневая (вверху) и объёмная (внизу) модели этана. В совокупности на рис. 14.9 и 14.10 приведено пять различных представлений молекулы этана. Лишь объёмная модель даёт близкое к реальности представление о пространственном строении молекулы. Остальные четыре модели преувеличивают для ясности расстояния между атомами. Атомы в шаростержневой и объёмной моделях на рис. 14.10 имеют одинаковые размеры. В шаростержневой модели связи изображены цилиндрами, а атомы отделены друг от друга связями. Важно понимать, что связи возникают за счёт образования молекулярных орбиталей. Электроны совместно используются атомами, которые не отделены друг от друга, как в шаростержневой модели или в других представлениях. Поверхность объёмной модели охватывает бо́льшую часть электронного распределения вероятностей. В объёмной модели атомы окрашены по-разному, чтобы их легче было различать.

Рис. 14.10. Модель этана: шаростержневая (вверху) и объёмная (внизу). Атомы в обеих моделях изображаются шарами одинакового размера

Нам понадобится обсудить ещё одну относительно простую молекулу — молекулу пропана, прежде чем углеводороды станут достаточно большими, чтобы начали обнаруживаться некоторые их общие свойства. Пропан состоит из трёх атомов углерода и восьми атомов водорода. Его химическая формула — C₃H₈. Это формула ничего не говорит о том, как соединены атомы. Её также можно записать в виде H₃C−H₂C−CH₃. При такой записи становится понятно, что атомы водорода соединены с атомами углерода. Атомы углерода соединены друг с другом одиночными связями. Концевые атомы углерода соединены с тремя атомами водорода и одним атомом углерода. Центральный атом углерода соединён с двумя атомами водорода и двумя атомами углерода. На рис. 14.11 приведены два представления молекулы пропана. На верхней диаграмме обозначены связи и углы между ними. Атомы углерода имеют тетраэдрическую конфигурацию связей с углами C−C−C и H−C−H, равными 109,5°. В нижней части рисунка представлена шаростержневая модель пропана.

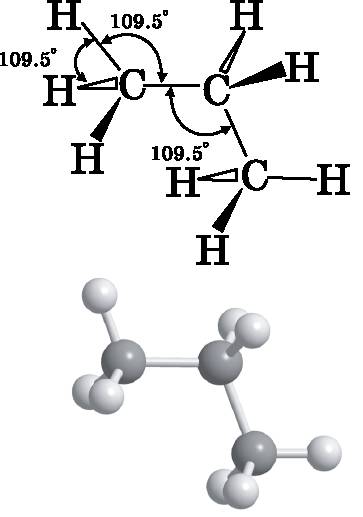Рис. 14.11. Диаграмма и шаростержневая модель пропана C ₃ H ₈ . Атомы углерода находятся в центрах тетраэдров

Большие углеводороды имеют множество структур

Для метана, этана и пропана существует лишь один способ, которым их атомы могут быть связаны друг с другом, и только одна пространственная конформация. Бутан и всё более крупные углеводороды имеют множество структурных конфигураций (способы, которыми атомы связаны друг с другом) и более одной пространственной конформации для конкретной структурной конфигурации. Бутан содержит четыре атома углерода. Его химическая формула — C₄H₁₀. Имеется две различные структурные формы бутана. Их называют структурными изомерами. Их молекулы содержат одинаковое число атомов углерода и водорода, но они имеют совершенно разную форму. Бутан может быть н-бутаном, что означает нормальный бутан. Если взять молекулу пропана и добавить к её концу ещё один атом углерода, получится н-бутан. О нём говорят как о линейной цепи, поскольку атомы углерода в нём связаны не более чем с двумя другими атомами углерода — по одному с каждой стороны. Его молекула, как видно из шаростержневой модели, в действительности не является прямой, поскольку каждый атом углерода имеет тетраэдрическую конфигурацию связей, образованных с использованием четырёх гибридных sp³-орбиталей.

На рис. 14.12 показано, что бутан имеет другой изомер, называемый изобутаном. В изобутане центральный атом углерода соединён с тремя другими атомами углерода и одним атомом водорода, а остальные атомы углерода соединены только с центральным атомом углерода и тремя атомами водорода каждый. Все четыре атома углерода используют для образования связей sp³-гибридизированные атомные орбитали и имеют тетраэдрическую конфигурацию. Об изобутане также говорят как о разветвлённой цепи. Тот факт, что бутан может при одинаковом числе атомов углерода и водорода иметь две разные структуры, очень важен. У молекулы с бо́льшим числом атомов углерода число возможных вариантов строения может быть намного больше двух.

В дополнение к двум структурным изомерам н-бутан имеет два конформера. Конформеры — это различные формы, конформации, одного и того же набора атомов, соединённых одним и тем же способом. Они различаются за счёт того, что вокруг одиночной связи C−C может происходить вращение.

Рис. 14.12. Два структурных изомера бутана C ₄ H ₁₀ . Вверху CH ₃ соответствует углероду, связанному с тремя атомами водорода. н-бутан— это линейная цепь в том смысле, что каждый атом углерода связан не более чем с двумя другими атомами углерода. Изобутан имеет разветвлённую структуру. Центральный атом углерода связан с тремя другими атомами углерода

На рис. 14.13 представлен н-бутан в двух конформациях, называемых транс и гош. Оба изображённых на рисунке конформера являются н-бутаном, поскольку атомы углерода соединены одинаковым образом. Если взять верхний конформер и выполнить поворот вокруг средней углерод-углеродной связи на 120° в направлении, указанном стрелкой, то получится гош-форма. У транс-конформера все атомы углерода лежат в одной плоскости. В гош-форме три атома углерода лежат в плоскости страницы, а четвёртый выступает над ней. В действительности существует и другая гош-форма, которая образуется путём поворота транс-формы вокруг средней C−C-связи на 120° в направлении, противоположном указанному стрелкой. В этом случае те же три атома углерода остаются в плоскости страницы, а четвёртый оказывается позади неё. Эти два гош-конформера в некотором смысле имеют одинаковую форму, но они не идентичны. Они подобны левой и правой перчаткам. Как и перчатки, эти две гош-формы нельзя совместить одну с другой. Они являются зеркальными копиями друг друга. Углеродная основа, которая может иметь левую и правую форму в зависимости от направления вращения, называется хиральной.

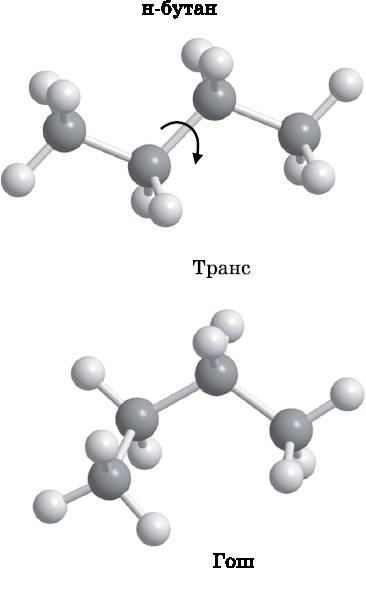Рис. 14.13. Два конформера н-бутана. Гош-форма получается из транс-формы вращением на 120° вокруг средней C−C-связи

Вращение вокруг одиночной C−C-связи, переводящее молекулу между транс- и гош-конформациями, в жидкости при комнатной температуре может происходить очень быстро. Согласно теории, подтверждённой недавними экспериментами с ультрабыстрым инфракрасным лазером, гош-транс-переходы занимают всего 50 пс (1 пикосекунда = 10⁻¹² сек), или 50 триллионных долей секунды. Поэтому в жидкости при комнатной температуре эти две формы бутана настолько быстро сменяют друг друга, что их невозможно изолировать в качестве отдельных молекул.

Двойные и тройные углерод-углеродные связи

Если вокруг одиночной C−C-связи совершить поворот очень легко, то для двойной или тройной углерод-углеродной связи это совсем не так. В главе 13 говорилось, что молекула O₂ имеет двойную связь, а молекула N₂ — тройную. Углерод-углеродные связи могут быть одиночными, двойными или тройными. Вращение вокруг двойной или тройной C−C-связи практически невозможно. Поэтому двойные связи могут фиксировать различные конформации молекул, имеющих одинаковые структурные изомеры. Как будет показано в главе 16, именно отсюда возникает термин «транс-жиры». Однако прежде, чем мы доберёмся до обсуждения таких больших молекул, как транс-жиры, нам надо поговорить о двойных и тройных C−C-связях.

В обсуждавшихся до сих пор соединениях углерод использует четыре sp³-гибридизированные атомные орбитали для создания четырёх одиночных σ-связей с другими атомами. В таких соединениях каждый атом углерода имеет тетраэдрическую конфигурацию четырёх связей. На рис. 14.3 изображена молекула формальдегида. Формальдегид содержит атом углерода с двойной связью. Чтобы показать, каким образом углерод создаёт одиночные, двойные и тройные связи, мы рассмотрим химические связи в этане, этилене и ацетилене. Эти три вещества имеют химические формулы H₃C−CH₃, H₂C=CH₂ и HC≡CH соответственно. Этан имеет одиночную связь, этилен — двойную, а ацетилен — тройную. На рис. 14.14 показано строение этих трёх молекул. В этане каждый атом углерода образует четыре связи в тетраэдрической конфигурации. В этилене каждый атом углерода образует три связи в форме треугольника, а в ацетилене атомы углерода образуют две связи, вытянутые в линию.

Хотя в каждой из трёх молекул два атома углерода связаны друг с другом, порядок их связи вносит большие различия. В табл. 14.1 приводятся значения длины и энергии C−C-связей для этих трёх молекул в зависимости от порядка связи. С увеличением порядка длина связи значительно сокращается, а энергия почти утраивается при переходе от одиночной связи к тройной.

Рис. 14.14. Этан: одиночная связь, тетраэдрическая конфигурация связей углерода. Этилен: двойная связь, треугольная конфигурация связей углерода. Ацетилен: тройная связь, линейная конфигурация связей углерода

Таблица 14.1. Одиночные, двойные и тройные C−C-связи

Порядок связи, Длина связи, Энергия связи ( Дж )

Этан, Одиночная (1), 1,54Å, 5,8∙10⁻¹⁹

Этилен, Двойная (2), 1,35Å, 8,7∙10⁻¹⁹

Ацетилен, Тройная (3), 1,21Å, 16∙10⁻¹⁹

Двойная углерод-углеродная связь — этилен

Для начала рассмотрим связь в молекуле этилена. Из рис. 14.15 видно, что углеродные центры здесь имеют треугольную форму. Как уже говорилось, для получения треугольной формы связей атом углерода будет использовать три sp²-гибридизированные атомные орбитали для образования МО (см. рис. 14.7). Углерод имеет четыре валентные орбитали, служащие для образования химических связей: 2s, 2p_x, 2p_y и 2p_z. В верхней части указанного рисунка молекула этилена располагается в плоскости xy. Таким образом, атомы углерода и водорода лежат в плоскости страницы, которая и есть xy. Чтобы образовать треугольную конфигурацию гибридных sp²-орбиталей, служащих для формирования трёх связей, оба атома углерода используют 2s-, 2p_x- и 2p_y-орбитали. С тремя гибридными sp²-орбиталями каждый атом углерода будет создавать три σ-связи: одну — с другим атомом углерода и две — с атомами водорода. Эти σ-связи показаны в верхней части рис. 14.15.

Когда углерод образует три гибридные sp²-орбитали из 2s-, 2p_x- и 2p_y-орбиталей, у него остаётся 2p_z-орбиталь, которая не принимает участия в σ-связывании. В верхней части рис. 14.15 2p_z-орбиталь направлена поперёк страницы, выступая над ней и позади неё. Каждый атом углерода имеет один неспаренный электрон на 2p_z-орбитали. В нижней части рисунка молекула этилена изображена повёрнутой. Сигма-связь показана линией, соединяющей атомы. Положительные лепестки 2p_z-орбиталей перекрываются конструктивно, и то же самое происходит с отрицательными лепестками. Две 2p_z-орбитали объединяются и образуют π-связывающую молекулярную орбиталь (см. рис. 13.3). Это π-связь, поскольку у неё нет электронной плотности на линии, соединяющей центры атомов углерода. Совокупный результат состоит в том, что два атома углерода имеют двойную связь, состоящую из σ-связи, образованной sp²-орбиталями каждого атома, и π-связью, образованной 2p_z-орбиталями тех же атомов.

Вращение вокруг двойной углерод-углеродной связи невозможно. Для него потребовалось бы, чтобы перекрытие двух 2p_z-орбиталей становилось всё хуже по мере увеличения угла поворота. При угле, равном 90°, две 2p-орбитали были бы направлены перпендикулярно друг другу и не давали бы никакого перекрытия. Такой поворот разрушил бы π-связь, на что потребовалось бы значительное количество энергии.

Рис. 14.15.Орбитали, образующие двойную связь в этилене. Вверху: каждый атом углерода использует три гибридные sp²-орбитали для образования трёх σ-связей в треугольной конфигурации. Страница соответствует плоскости xy, ось z направлена перпендикулярно этой плоскости. Внизу: каждый атом углерода имеет 2p_z-орбитали, которые не используются в sp²-гибридизации. 2p_z-орбитали объединяются и порождают π-связывающую молекулярную орбиталь, которая даёт вторую связь между атомами углерода

Как уже говорилось, измерения и теория позволили определить, что молекула бутана в жидкой фазе поворачивается вокруг одиночной C−C-связи примерно за 50 пс. Для этана это время составляет около 12 пс. Бутан вращается вокруг одиночной C−C-связи медленнее этана, поскольку содержит две дополнительные метильные группы (CH₃) — по одной с каждой стороны от двух центральных атомов углерода. Если поместить этилен в такую же жидкую среду при комнатной температуре, то, по грубым оценкам, потребуется около ста миллиардов лет для того, чтобы совершить поворот вокруг двойной связи, поскольку на разрушение π-связи требуется огромное количество энергии. Таким образом, в любом практическом смысле двойная связь (как и тройная) препятствует вращательной изомеризации между конформерами, которые различаются конфигурацией относительно двойной связи.

Тройная углерод-углеродная связь — ацетилен

Ацетилен образует тройную связь между атомами углерода, во многом аналогичную двойной связи в этилене. Каждый атом углерода имеет для образования химических связей четыре атомные орбитали: 2s, 2p_x, 2p_y и 2p_z. Молекула ацетилена линейная (см. рис. 14.14). Примем линию, вдоль которой выстроена молекула, за ось x. Тогда каждый атом углерода образует две гибридные sp-орбитали из своих 2s- и 2p_x-орбиталей. Эти две гибридные sp-орбитали атома углерода служат для образования двух σ-связей: одной — с другим атомом углерода и одной — с атомом водорода. В результате остаются неиспользованными две 2p-орбитали у каждого атома углерода — 2p_y и 2p_z. 2p_z-орбитали атомов углерода образуют одну π-связывающую МО, a 2p_y-орбитали — другую. В результате два атома углерода оказываются соединены тройной связью: одной σ-связью и двумя π-связями.

В последующих главах мы будем обсуждать ряд типов молекул, таких, например, как спирты, органические кислоты, крупные углеводороды и углеродсодержащее топливо — уголь, нефть и природный газ. Обсуждение небольших спиртовых молекул позволит нам понять, что такое спирты и почему небольшие различия в их строении могут иметь огромное значение, если вы решите выпить что-то, отличное от этанола (спирта, содержащегося в пиве). Эти идеи позволят нам понять, почему одни молекулы растворимы в воде, а другие нет и каким образом мыло (разновидность крупных органических молекул) позволяет растворяться в воде нерастворимым жирам. В связи с вопросом о жирах и транс-жирах мы разберёмся в том, насколько важна неспособность двойных связей подвергаться вращательным структурным изменениям. Мы обсудим, что происходит, когда горит основанное на углероде топливо и почему при одинаковом количестве выделяемой энергии одно топливо даёт больше парникового углекислого газа, а другое — меньше. То, что углекислый газ является парниковым, хорошо известно, но почему? Мы увидим, как сочетание двух фундаментальных квантовомеханических эффектов делает диоксид углерода мощным парниковым газом.

15. Пиво и мыло

В этой главе мы рассмотрим несколько типов молекул, чтобы увидеть, как различия в их природе влияют на химические процессы. Прежде всего, мы займёмся спиртами. Спирт — это органическая молекула, которая содержит химическую группу определённого типа. Молекула спирта может быть относительно маленькой, как, например, у этилового спирта, который химики обычно называют этанолом. Этанол — это спирт, содержащийся в пиве, вине и водке. Однако крупные и важные биологические молекулы, например холестерин, также являются спиртами. Такими крупными молекулами мы займёмся в главе 16. А сейчас разберёмся, почему этанол растворяется в воде, как он превращается в уксус и какие химические реакции в вашем теле делают метанол (древесный спирт) ядовитым, в то время как этанол безопасен, по крайней мере в умеренных количествах. Опираясь на механизм, который позволяет некоторым молекулам растворяться в воде, мы рассмотрим строение молекул мыла и масла, чтобы понять, почему для того, чтобы удалить загрязнения с посуды и смыть их в канализацию, нужно мыло.

Спирты

Этанол — это этан (см. рис. 14.10), в котором один из атомов водорода заменён OH-группой, называемой также гидроксильной группой. Химическая формула этанола H₃CH₂COH. На рис. 15.1 изображены диаграмма и шаростержневая модель этанола. В этаноле, как и в этане, атомы углерода используют четыре гибридные sp³-орбитали для образования тетраэдрической конфигурации связей. Кислород также использует четыре sp³-гибридизированные орбитали. Одна из них служит для того, чтобы соединиться с атомом углерода, ещё одна используется для связи с водородом, а остальные две содержат неподелённые электронные пары. Эти неподелённые пары не показаны на схеме и в шаростержневой модели на рис. 15.1. (На рис. 14.2 изображены неподелённые пары кислорода в молекуле воды.)

Рис. 15.1. Схема молекулы этанола (этилового спирта), демонстрирующая, как в этой молекуле соединены атомы (вверху), и её шаростержневая модель (внизу). Атомы водорода показаны светло-серым тоном, углерод — серым, а кислород — чёрным

Обратите внимание, что в шаростержневой модели этанола атом водорода, соединённый с кислородом, заметно меньше атомов водорода, соединённых с атомами углерода. Обратившись к Периодической таблице (см. главу 11), мы узнаём, что кислород в действительности стремится захватить электроны, чтобы получить замкнутую, как у неона, конфигурацию оболочки. Однако совместное использование электронов в химической связи кислорода и углерода не вполне равноправное. Кислород очень сильно притягивает электроны и перетаскивает к себе часть электронной плотности от водорода. Дополнительная электронная плотность придаёт кислороду частичный отрицательный заряд, а водород из-за потери электронной плотности приобретает частичный положительный заряд. Эта потеря электронной плотности приводит к уменьшению размера электронного облака атома водорода, что и отражено на рисунке относительно малым размером сферы, соответствующей атому водорода, связанному с кислородом. Углерод и водород, образующие ковалентную связь, почти одинаково притягивают электроны. Поэтому они делят электроны почти поровну. Таким образом, в среднем электронная плотность у водорода, связанного с углеродом, больше, чем у водорода, связанного с кислородом. В общем случае спирт — это молекула, в которой есть атом углерода с присоединённой к нему OH-группой, и кроме неё данный атом углерода связан только с водородом или другими атомами углерода.

При комнатной температуре этанол жидкий, а не газообразный

При комнатной температуре этан является газом, а этанол — жидкостью. Для сжижения этана его надо охладить до −89 °C, а этанол надо нагреть до 78 °C, прежде чем он закипит и превратится из жидкости в газ. Этан и более крупные углеводороды, входящие в состав нефти, нерастворимы в воде, тогда как этанол и более крупные спирты в воде растворяются. Этан и этанол имеют почти одинаковые размеры и похожие формы. Так почему же этанол, в отличие от этана, растворяется в воде и находится в жидком состоянии при комнатной температуре?

Как уже было кратко отмечено, имеющаяся у этанола гидроксильная группа (OH) привносит два небольших изменения. Атом кислорода несёт частичный отрицательный заряд, а атом водорода — частичный положительный. Схематически это обозначается так: O^δ−−H^δ+ (греческая буква δ «дельта» используется здесь в значении «частичный»). За дельтой следует знак электрического заряда атома. Величина электронной плотности, передаваемая от атома H к атому O, очень мала — много меньше заряда одного электрона, который передаётся в такой соли, как NaCl, где ионы обозначаются Na⁺ и Cl⁻. Связь между кислородом и водородом в основном ковалентная, а не ионная, как в NaCl. Однако частичные заряды на атомах O и H невероятно важны. Они возникают из-за особенностей молекулярных орбиталей, отвечающих за ковалентную связь кислорода и водорода. Эти частичные заряды приводят к тому, что этанол оказывается жидкостью. Если позволить себе лёгкое преувеличение, то можно сказать, что без того же рода частичных зарядов на атомах кислорода и водорода в молекулах воды жизнь не могла бы существовать.

Этанол является жидким, поскольку описанные небольшие изменения приводят к появлению своего рода химических взаимодействий между молекулами, которые называются водородными связями. Водородные связи намного — примерно в десять раз или более — уступают по силе настоящим ковалентным химическим связям. Чтобы точно описать образование водородных связей, необходима квантовая теория, однако получить представление на качественном уровне можно, рассматривая электростатическое взаимодействие между частичными зарядами. Водородная связь образуется, когда частично положительный атом водорода в одной молекуле притягивается к частично отрицательному атому кислорода в другой молекуле. За счёт этого притяжения атом водорода одной молекулы этанола тяготеет к строго определённому положению относительно атома кислорода другой молекулы этанола. Это притяжение удерживает молекулы этанола вместе и делает вещество жидким при комнатной температуре. В этане такого относительно сильного межмолекулярного взаимодействия нет.

Тепло — это форма кинетической энергии. При повышении температуры беспорядочное движение молекул усиливается. В этане молекулы не испытывают сильного притяжения друг к другу. При комнатной температуре тепловые движения не позволяют молекулам этана соединяться, и поэтому этан является газом. Представьте себе, что вы, держа за руки другого человека, побежали с ним в противоположных направлениях. Если ваше рукопожатие слабое, оно разорвётся, и вы разбежитесь, как молекулы этана. Если же вы держитесь очень крепко, то останетесь вместе и станете двигаться, будто связаны друг с другом, как молекулы этанола.

Рис. 15.2. Четыре молекулы этанола связаны в цепочку. Атомы кислорода на этом рисунке изображены тёмно-серыми. Кислород, помимо связанных с ним атомов водорода и углерода, имеет две неподелённые пары. Штриховые линии показывают водородные связи, которые идут от атома H гидроксильной группы одной молекулы этанола к неподелённым парам кислорода другой молекулы этанола

На рис. 15.2 изображены четыре молекулы этанола, соединённые в цепочку водородными связями. Штриховые линии идут от водорода в OH-группе одной молекулы этанола к неподелённой паре на атоме кислорода другой молекулы этанола. Неподелённая пара имеет высокую электронную плотность, так что частично положительный атом H притягивается к электронам неподелённой пары кислорода. Это продолжается от одной молекулы этанола к другой, и так образуется цепочка. Жидкий этанол состоит из цепочек молекул, которые соединяются водородными связями. Водородные связи делают этанол жидким при комнатной температуре, но они относительно слабые. Эти связи постоянно разрушаются и реорганизуются, но в среднем каждая молекула этанола имеет водородную связь (H-связь) с одной или несколькими другими молекулами этанола. Однако если достаточно сильно нагреть этанол, тепловые движения начнут разрушать H-связи, и молекулы будут разлетаться. Температура, при которой тепловой энергии достаточно для разделения молекул этанола, — это и есть точка кипения, равная 78 °C. При этой и более высокой температуре этанол становится газом.

Вода образует водородные связи

Вернёмся к вопросу о том, почему водородные связи необходимы для жизни. Вода (H₂O) имеет очень маленькую молекулу. По молекулярной массе она сравнима с кислородом O₂, азотом N₂ и метаном CH₄, которые при комнатной температуре являются газами. Вода содержит один атом кислорода, связанный с двумя атомами водорода. Как и в случае с этанолом, кислород создаёт ковалентные связи с атомами водорода, но в ковалентной связи O−H электроны делятся не идеально поровну. В молекуле воды кислород перетягивает часть электронной плотности от атомов H. Демонстрирующая это схема молекулы воды выглядит так: H^δ+−O^δ−−H^δ+. Частично положительные атомы водорода одной молекулы воды притягиваются к частично отрицательным атомам кислорода другой молекулы. Одна молекула воды может создать до четырёх водородных связей.

Схематическая иллюстрация водородных связей воды представлена на рис. 15.3. Центральная молекула воды имеет четыре водородные связи с окружающими четырьмя молекулами. Две гидроксильные группы этой центральной молекулы воды связаны водородными связями с двумя атомами кислорода других молекул воды. При этом гидроксильные группы двух других молекул воды образуют водородные связи с атомом кислорода центральной молекулы. В отличие от модели молекулы, представленной на рис. 15.3, водородные связи не ограничиваются этими пятью молекулами. Каждая из четырёх внешних молекул сама создаёт около четырёх связей с другими молекулами воды. В результате получается сеть водородных связей.

Рис. 15.3. Центральная молекула воды связана водородными связями с четырьмя окружающими молекулами воды. Атомы водорода из двух гидроксильных групп центральной молекулы воды связаны с двумя атомами кислорода других молекул, а атом кислорода центральной молекулы воды притягивает две гидроксильные связи двух других молекул воды

Тепла при комнатной температуре довольно много, так что водородные связи между одними молекулами воды постоянно разрушаются и вместо них образуются водородные связи с другими молекулами воды. Поэтому сеть водородных связей не является статичной. Она постоянно трансформируется и реорганизуется. Характерный временной масштаб этой реорганизации водородных связей был измерен при помощи сверхскоростной инфракрасной спектроскопии и составляет примерно 3 пс (1 пс = 10⁻¹² сек)^{25}.

Жизнь основана на химических реакциях, которые протекают в воде. Космический аппарат, отправленный недавно на Марс, ищет не столько непосредственные свидетельства существования в прошлом жизни, сколько признаки существования в прошлом жидкой воды. Жидкая вода имеет настолько фундаментальное значение для существования жизни, что её присутствие является необходимым и, возможно, достаточным для этого условием. Удивительные свойства воды, которые чрезвычайно важны для протекания биохимических реакций, являются следствием строения этой сети водородных связей и её способности к реорганизации. Свойства воды позволяют протекать огромному числу химических процессов, необходимых для жизни. Например, именно в воде происходит фолдинг белков^{26}.

Белки — это очень большие и чрезвычайно сложные молекулы, ответственные за большинство химических процессов в наших телах. Когда белки химически производятся другими белками, то первоначально они не обладают правильной конфигурацией для выполнения своих функций. Они находятся в развёрнутом состоянии. У белков есть участки, которые вскоре образуют водородные связи с водой, и участки, которые больше похожи на углеводороды и не хотят смешиваться с водой. Белок меняет своё строение, складываясь таким образом, чтобы гидрофильные (любящие воду) участки находились снаружи и контактировали с водой, образуя с ней водородные связи, а гидрофобные (избегающие воды) участки располагались внутри, вдали от воды. Такое избирательное взаимодействие с водой — важная движущая сила, помогающая белкам принимать правильную форму, необходимую для выполнения их функций. Именно благодаря тому, что вода может легко реорганизовывать свою сетевую структуру, создавая и разрушая водородные связи, она легко поддерживает структурные преобразования белков и огромное число других химических процессов, которые протекают в живых организмах.

Вода — великий растворитель

Одно из свойств воды — её способность растворять очень широкий набор химических соединений. Мы уже обсуждали, что соль NaCl растворяется в воде с образованием ионов Na⁺ и Cl⁻. Положительные ионы окружены частично отрицательными атомами кислорода воды, а отрицательные ионы — частично положительными атомами водорода воды. Соль растворяется благодаря способности воды хорошо взаимодействовать как с катионами, так и с анионами. Вода также может растворять очень широкий набор органических веществ. Вода не растворяет углеводороды вроде этана, но она растворяет такие органические молекулы, как этанол, содержащий гидроксильную группу (−OH) или другие группы, имеющие слабо или сильно заряженные участки. Вода растворяет этанол, образуя водородные связи с гидроксильной группой этанола. В чистом этаноле водородные связи между молекулами этанола образуют цепочки, изображённые на рис. 15.2. Когда этанол попадает в воду, вода может образовывать водородные связи с гидроксильными группами этанола, включая молекулы этанола в единую сеть водородных связей. Водка, по сути, представляет собой этанол в воде. Вино — это вода с меньшим количеством этанола, чем в водке. Вино также содержит большие органические молекулы, придающие красному вину его цвет, а всем винам — характерные для каждого из них аромат и оттенки вкуса.

Этанол участвует в химических реакциях с кислородом

Если вино слишком долго находится на воздухе, оно портится, превращаясь в уксус. Уксус можно целенаправленно получить путём сбраживания вина. Химические реакции, превращающие вино в уксус, в действительности осуществляются уксуснокислыми бактериями (Acetobacteraceae), которые в присутствии кислорода способны превращать этанол в уксусную кислоту. Этот процесс протекает как последовательность двух химических реакций:

CH₃CH₂OH → CH₃CHO + H₂,

2CH₃CHO + O₂ → 2CH₃COOH.

Сначала этанол (CH₃CH₂OH) превращается в ацетальдегид и газообразный водород (верхняя строка), а затем две молекулы ацетальдегида и одна молекула кислорода (два атома кислорода) превращаются в две молекулы уксусной кислоты, которая и есть уксус. Строение этанола изображено на рис. 15.1, а на рис. 15.4 показано строение ацетальдегида (вверху) и уксусной кислоты (внизу). В ацетальдегиде и уксусной кислоте атом углерода, обозначенный C₁, образует метильную группу. C₁ связан с тремя атомами водорода и атомом углерода C₂. В ацетальдегиде атом C₂ также связан с одним атомом водорода и двойной связью с кислородом.

Рис. 15.4. Ацетальдегид (вверху) и уксусная кислота (внизу). Атомы кислорода изображены в виде тёмно-серых сфер. Атом углерода C ₂ в ацетальдегиде связан с C ₁ , с водородом и двойной связью с кислородом. Атом C ₂ в уксусной кислоте связан с C ₁ , двойной связью с кислородом и одиночной связью с другим атомом кислорода, входящим в состав гидроксильной группы

В общем случае в альдегиде есть атом углерода, соединённый двойной связью с кислородом и одиночными связями с водородом и другим углеродом. Так, в формальдегиде (см. рис. 14.3) вместо связи с другим атомом углерода атом C₂ связан со вторым атомом водорода. Атом C₂ использует три гибридные sp²-орбитали для образования трёх σ-связей и дополнительную 2p-орбиталь для объединения с 2p-орбиталью кислорода и формирования π-связи в составе двойной связи. Как видно из верхнего уравнения химической реакции и строения этанола, показанного на рис. 15.1, этанол превращается в ацетальдегид, избавляясь от двух атомов водорода, что приводит к образованию ацетальдегида и молекулы H₂. Две молекулы ацетальдегида присоединяют каждая по одному атому кислорода из молекулы O₂, иполучаются две молекулы уксусной кислоты (внизу на рис. 15.4). В уксусной кислоте атом C₂ связан с двумя атомами кислорода. С одним из них он связан двойной связью, а с кислородом из гидроксильной группы −OH — одиночной.

Уксусная кислота — это органическая кислота, относящаяся к классу карбоновых кислот. Группа −COOH является кислотной. Простейшее определение кислоты — это вещество, которые при попадании в воду приводит к появлению ионов водорода H⁺. Соляная кислота имеет формулу HCl. Как и молекула NaCl, в воде молекула HCl распадается на ионы H⁺ и Cl⁻. Молекула соляной кислоты HCl полностью диссоциирует на ионы. Она классифицируется как сильная кислота, поскольку на каждую молекулу HCl, попавшую в воду, появляется один ион H⁺. H⁺ связывается (через сольватирование) с молекулами воды. Частично отрицательные атомы кислорода в молекулах воды окружают ион H⁺. Реакцию кислотной диссоциации уксусной кислоты в воде можно записать следующим образом:

Группа −COOH — это органическая кислотная группа. Такая группа ионизируется с образованием, как показано, ионов −COO⁻ и H⁺. Согласно схеме, отрицательный заряд привязан к одному из атомов кислорода. В действительности он поровну распределён между обоими атомами кислорода. Это равное распределение изображают на схеме следующим образом:

Пунктирная кривая указывает, что молекулярная орбиталь, содержащая электрон, придающий отрицательный заряд, распределена по обоим атомам кислорода. Каждый из них может рассматриваться как носитель половины отрицательного заряда. Органические кислоты очень хорошо растворяются в воде. Этанол растворим, поскольку кислород из гидроксильных групп имеет небольшой отрицательный заряд, который приводит к образованию водородных связей с молекулами воды. Недиссоциированная уксусная кислота имеет два атома кислорода с частичными зарядами, которые могут образовывать водородные связи с водой. Диссоциированная уксусная кислота имеет два атома кислорода с половинным отрицательным зарядом, что приводит к эффективному образованию водородных связей с водой.

Органические кислоты, такие как уксусная кислота, являются слабыми. В воде лишь небольшая часть молекул уксусной кислоты ионизируется с образованием иона H⁺ и уксусного аниона. При растворении в литре воды 60 граммов уксусной кислоты ионами становится лишь около 0,4 % молекул. Эта концентрация примерно соответствует обычному столовому уксусу. Именно уксусная кислота придаёт уксусу его характерный вкус. Органические кислоты очень широко распространены в химии и биологии. Все белки состоят из комбинаций 20 аминокислот. До вступления в реакцию образования белка каждая аминокислота относится к определённому виду органических кислот и содержит органическую кислотную группу −COOH.

Метанол крайне ядовит

Метанол — это самая маленькая спиртовая молекула. Этанол — это этан, в котором один атом водорода заменён гидроксильной группой −OH. Метанол — это метан, в котором водород заменён гидроксилом. Если этанол можно употреблять внутрь в разумных количествах без тяжёлых последствий, то метанол крайне токсичен. Его также называют древесным спиртом, и он нередко встречается в качестве примеси в самогоне. Его смертельная доза составляет всего 20 мл (миллилитров), а доза 15 мл может вызвать слепоту. Пятнадцать миллилитров — это одна столовая ложка. Стакан вина содержит около двух столовых ложек этанола. Так что замена этанола на метанол в одном стакане вина может вызвать слепоту и смерть. Это поразительно, поскольку этанол отличается от метанола лишь одной дополнительной метильной группой (−CH₃).

Ядовит не сам по себе метанол, а продукты его метаболизма. У человека и других живых организмов спирты превращаются в другие вещества посредством энзимов (белков, отвечающих за химические реакции), которые называются алкогольдегидрогеназами. У человека эти энзимы содержатся в печени и слизистой оболочке желудка. По-видимому, эти энзимы в пищеварительном тракте появились в ходе эволюционного развития для разложения спиртов, которые вырабатываются бактериями или являются естественными составляющими некоторых видов пищи. Этанол сначала превращается в ацетальдегид, а затем в уксусную кислоту, как это обсуждалось выше в связи с рис. 15.4, на котором показана структура этих двух молекул. Ацетальдегид и уксусная кислота безопасны для организма, который легко от них избавляется. Более крупные спиртовые молекулы также превращаются сначала в альдегиды, а затем в органические кислоты, которые легко удаляются из тела, не причиняя ему вреда. Однако метанол превращается алкогольдегидрогеназами в формальдегид, а затем в муравьиную кислоту.

Строение формальдегида представлено на рис. 14.3. Формальдегид подобен ацетальдегиду, за исключением того, что атом углерода C₂ в ацетальдегиде (см. рис. 15.4, вверху) связан с одним атомом водорода, а не с метильной группой (C₁ на рис. 15.4). Муравьиная кислота подобна уксусной кислоте (рис. 15.4, внизу), но вновь атом C₂ связан с водородом, а не с метильной группой. Муравьиная кислота и особенно — формальдегид являются высокотоксичными веществами. Они повреждают сетчатку и зрительный нерв, приводя к неизлечимым поражениям зрения и слепоте. Однако муравьиная кислота также вызывает серьёзную кислотную интоксикацию, которая включает нарушение работы энзимов, расщепляющих углеводороды. Относительно небольшие концентрации формальдегида и муравьиной кислоты, а также других производных от них метаболитов могут привести к смерти.

Мыло

Как мы выяснили, этанол и органические кислоты вроде уксусной кислоты очень хорошо растворяются в воде, поскольку органические группы, содержащие кислород, могут создавать водородные связи с молекулами воды. Напротив, этан, хотя и очень похож на этанол, не растворяется в воде, поскольку не имеет кислородсодержащей группы, способной образовывать водородные связи. Этан — это углеводород, то есть он состоит только из атомов водорода и углерода. Метан и этан — газы. Более крупные углеводороды, начиная с пентана (пять атомов углерода), являются жидкостями при комнатной температуре. Наименьшие из этих жидких углеводородов, такие как пентан и октан (входящий в состав бензина), — очень текучие жидкости, то есть у них низкая вязкость.

Крупные углеводороды — это масло и жир

С увеличением числа атомов углерода жидкие углеводороды становятся всё более вязкими. Мазут^{27}, используемый для отопления во многих американских домах, состоит из смеси углеводородов, имеющих обычно от 14 до 20 атомов углерода. При комнатной температуре масло вполне текуче, но его вязкость намного больше, чем у бензина. Жир состоит из по-настоящему крупных углеводородов. Они очень вязкие и при комнатной температуре не текут.

Рис. 15.5. Модели н-тетрадекана C ₁₄ H ₃₀ : шаростержневая (вверху) и объёмная (внизу). Молекула содержит 14 атомов углерода, соединённых друг с другом без ветвления

Углеводороды, составляющие мазут, при комнатной температуре являются жидкими, но они нерастворимы в воде. Молекулы с 14 атомами углерода — это самые лёгкие компоненты мазута. На рис. 15.5 изображена молекула н-тетрадекана. Декан содержит десять (дека) атомов углерода. В тетрадекане на четыре (тетра) атома углерода больше. Буква «н» (нормальный) означает, что все атомы углерода выстроены друг за другом без ветвления, то есть каждый атом углерода связан не более чем с двумя другими. В верхней части рисунка приведена шаростержневая модель н-тетрадекана. Однако важно помнить, что электронная плотность заполняет всё окружающее атомы пространство. В нижней части рисунка представлена объёмная модель н-тетрадекана.

Крупные углеводороды могут иметь много разных структур

Многие другие углеводороды содержат по 14 атомов углерода. Они являются ветвящимися. На рис. 15.6 представлены шаростержневая (вверху) и объёмная (внизу) модели одного из них — 2,8-диметилдодекана. Додекан содержит 12 атомов углерода. Две дополнительные метильные группы ответвляются от основной цепочки у второго и восьмого слева атомов углерода. И н-тетрадекан, и 2,8-диметилдодекан являются структурными изомерами. У них одинаковое число атомов водорода и углерода, но никакие повороты вокруг связей не могут преобразовать один в другой. И н-тетрадекан, и 2,8-диметилдодекан имеют множество конформеров, то есть, поворачивая молекулы вокруг одиночных углерод-углеродных связей, можно получить различные формы молекул без изменения схемы соединения атомов углерода. Структурные изомеры и конформеры уже обсуждались на примере бутана (см. рис. 14.12 и 14.13).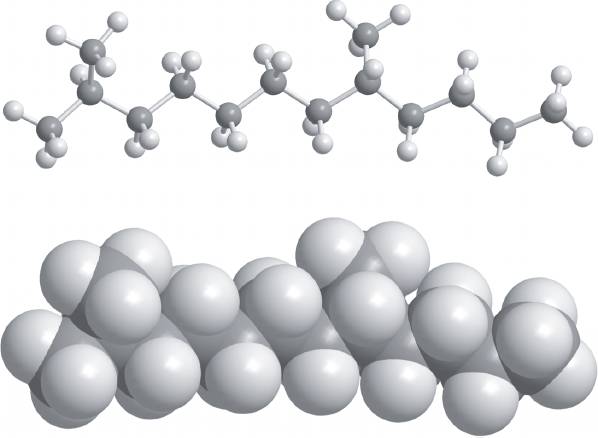

Рис. 15.6. 2,8-диметилдодекан C ₁₄ H ₃₀ : шаростержневая модель (вверху) и объёмная модель (внизу). Молекула содержит 14 атомов углерода. Имеется цепочка из 12 атомов углерода с двумя метильными группами, ответвляющимися от неё у второго и восьмого слева атомов углерода

Нефтепродукты и вода не смешиваются

Мазут является относительно вязкой жидкостью, хотя молекулы углеводородов относительно слабо притягиваются друг к другу. Большое число размеров, структурных изомеров и конформеров приводит к тому, что молекулы запутываются, и в результате возрастает вязкость. При попадании нефтепродуктов в воду они всплывают на поверхность. Если всё хорошенько взболтать, то кажется, что они на время смешиваются. Однако если дать смеси отстояться, нефтепродукты вновь отделяются от воды и всплывают на поверхность. С подобным эффектом знаком каждый, кто делал заправку для салата из уксуса и растительного масла. Вы смешиваете оливковое масло, уксус и, возможно, немного воды и встряхиваете смесь. Если оставить её постоять, то оливковое масло всплывёт наверх. В магазинные салатные заправки из масла и уксуса добавляют эмульгаторы, которые предотвращают разделение масла и уксуса.

Эмульгаторы очень похожи на мыло, с которым мы скоро познакомимся ближе. Мы уже знаем, что атом кислорода в молекуле воды частично отрицательный и притягивается к атомам, заряженным положительно или, по крайней мере, имеющим частичный положительный заряд. Атомы водорода в молекулах воды частично положительны и притягиваются к отрицательно заряженным или частично отрицательно заряженным атомам. Углеводороды состоят из атомов углерода и водорода, которые по заряду являются практически нейтральными. Поэтому молекулы воды притягиваются друг к другу значительно сильнее, чем к маслу. Как результат — масло не растворяется в воде.

Строение молекул мыла

Мыло делает масло растворимым в воде. В мыле и моющих средствах используется много разных молекул. Более строгое название для молекул мыла — поверхностно активные вещества (ПАВ). Хотя химическая природа и строение ПАВ очень сильно варьируются, все ПАВ обладают некоторыми общими свойствами. Часть молекулы ПАВ, если взять её отдельно, была бы очень хорошо растворимой в воде, а другая часть, взятая сама по себе, прекрасно растворялась бы в масле и жирах.

Одна из таких молекул — н-гептадеканацетат натрия; её шаростержневая и объёмная модели изображены на рис. 15.7. Углеводород н-гептадекан — это неветвящаяся 17-атомная цепочка. Эта углеводородная часть молекулы изображена в виде конкретного конформера с парой поворотов вокруг углерод-углеродных связей, что приводит к изогнутой форме. Тетрадекан, изображённый на рис. 15.5, весь находится в транс-конформации. У него нет никаких поворотов, привносящих элементы гош-конформации. У больших углеводородов много разных конформеров, между которыми они могут переходить. Сам по себе гептадекан может быть одним из компонентов мазута.

Рис. 15.7.Гептадеканацетат натрия C₁₈H₃₇COO−Na⁺: шаростержневая модель (вверху) и объёмная модель (внизу). Диссоциированный ион натрия не показан. Молекула содержит 19 атомов углерода. В ней есть цепочка из 17 атомов углерода и на её конце ацетатная группа. Обозначение δ⁻ указывает, что каждый из атомов кислорода (самые тёмные сферы) несёт примерно половинный отрицательный заряд

Углеводород н-гептадекан присоединяется к ацетатной группе или ацетатному аниону. Ацетатная группа состоит из двух последних атомов углерода и двух атомов кислорода в правой части молекулы на рис. 15.7. Ацетатный анион изображён на с. 269 на химической диаграмме, описывающей диссоциацию уксусной кислоты. Там катионом при диссоциации был ион H⁺. Здесь же катион — это ион натрия Na+, который на рис. 15.7 не показан. Ацетат натрия представляется следующей диаграммой:

Ацетат натрия — это натриевая соль, подобно поваренной соли NaCl. В данном случае анион является органическим в отличие от элементарного аниона Cl⁻. Ацетат натрия полностью растворяется в воде, как и соль NaCl.

В воде мыло образует мицеллы

Таким образом, молекула н-гептадеканацетата натрия состоит из длинной углеводородной цепочки, которая не будет растворяться в воде, и ацетата натрия, который в воде легко растворяется.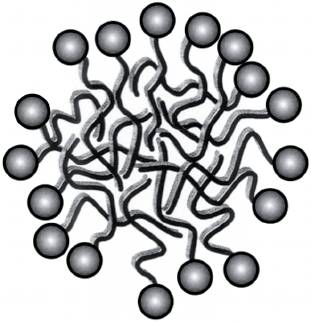

Рис. 15.8. Схематическое изображение сферической мицеллы. Шарики символизируют ацетатные группы либо другие заряженные или гидрофильные части молекул ПАВ. Гидрофильную часть молекулы ПАВ нередко называют головной группой. Волнистыми линиями показаны гидрофобные углеводородные хвосты ПАВ. Головные группы очень хорошо растворимы в воде и образуют внешнюю оболочку. Углеводородные хвосты избегают контакта с водой и группируются друг с другом, образуя нанокапельку масла, называемую ядром мицеллы. Образование мицелл позволяет мылу легко растворяться в воде

Что случится, если поместить значительное количество мыла (в данном случае н-гептадеканацетата натрия) в воду, не содержащую масла и жира? Углеводородные части молекул не любят воду, так что они будут её избегать. Чистый углеводород н-гептадекан полностью отделился бы от воды и всплыл на поверхность. Однако части с ацетатом натрия вода нравится. Эта часть будет диссоциировать на ацетат-анион и натриевый катион, и оба они будут активно взаимодействовать с молекулами воды. Мицеллы — это наномасштабные образования, то есть имеющие размеры порядка нескольких нанометров. Обычная форма мицеллы сферическая или близкая к сферической, хотя есть и другие разновидности в зависимости от ПАВ и его концентрации в воде. Обычно они имеют размеры около 10 нанометров (10 триллионных долей метра) в диаметре. Размеры мицелл определяются размерами и строением молекул ПАВ.

Мыло растворяет жирные загрязнения

Теперь рассмотрим, что происходит, когда посуда или руки, испачканные жиром или маслом, попадают в мыльную воду. Чистую воду углеводороды на их поверхности отталкивали бы. Однако наличие в воде мыльных мицелл всё меняет. Заряженные головные группы мицелл приходят в контакт с жирной поверхностью. Они стремятся избежать жира, который заставляет мицеллы открываться, выставляя к жиру углеводородные хвосты ПАВ. Эти хвосты ПАВ с удовольствием погружаются в жирные загрязнения и запутываются в них. За счёт механических движений эти маслянистые углеводороды отрываются от остальной жирной поверхности. Головные группы ПАВ смыкаются вокруг ядра, приводя к реорганизации мицеллы. Однако некоторые углеводороды, составлявшие жирное загрязнение, оказываются захваченными в ядре мицеллы.

Удержание углеводородов внутри мицеллы схематически изображено на рис. 15.9. Углеводородные хвосты ПАВ обозначены двойными линиями, а жирные углеводороды — одиночными линиями с точками. Молекулы жирных загрязнений остаются в ядре мицеллы в качестве части масляной нанокапли. Эти дополнительные углеводороды в её ядре делают мицеллу крупнее. Чтобы полностью покрыть увеличившуюся нанокаплю, к мицелле добавляются новые молекулы ПАВ, содержащиеся в воде. Заряженные главные группы одной мицеллы отталкивают другие, предотвращая тем самым слияние содержащихся в них загрязнений с образованием нерастворимых в воде комков.

Рис 15.9. Схематическое изображение маслянистых углеводородных загрязнений (одиночные узорчатые линии), захваченных мыльной мицеллой

Первые свидетельства о производстве мылоподобных веществ относятся ещё к 2800 году до нашей эры. Настоящее мыло — практически такое же, каким мы пользуемся сегодня, — было изготовлено химиками исламского мира в VII веке. Мы часто слышим о наступлении эпохи нанотехнологий, в которых нанометрового размера конструкции из молекул и атомов могут выполнять различные очень тонкие задачи. В этом смысле весьма примечательно, что мыло в воде является наноматериалом. ПАВ образует нанометрового размеры мицеллы, которые захватывают жировые загрязнения. Эти мицеллы, содержащие углеводороды, растворимы в воде, что позволяет нам отмывать самостоятельно нерастворимые в воде молекулы.

16. В жирах важны двойные связи

В этой главе мы, опираясь на развитые ранее идеи, поговорим о некоторых крупных молекулах, часто встречающихся в повседневной жизни. Мы, наконец, добрались до таких веществ, как насыщенные жиры, ненасыщенные жиры, транс-жиры и холестерин. Что они собой представляют и чем различаются? Как их влияние на здоровье связано с их молекулярным строением?

Из чего состоят жировые молекулы?

Слыша слово «жир», вы, вероятно, думаете о сливочном масле, сале, оливковом или хлопковом масле. Каждое из них в действительности представляет собой смесь различных жиров. На рис. 16.1 изображена одна конкретная молекула жира^{28}. Это стеариновая кислота. Она представляет собой длинную углеводородную цепочку с кислотной органической группой на конце. Стеариновая кислота содержит 18 атомов углерода. Крайний справа атом углерода входит в состав органической кислотной группы. На рис. 15.4 (внизу) изображена молекула уксусной кислоты, которая представляет собой кислотную группу с присоединённой к ней метильной группой. На рис. 15.5 изображён тетрадекан — входящий в состав нефти углеводород, который содержит 14 атомов углерода. Стеариновая кислота подобна уксусной кислоте, но вместо одиночной метильной группы к кислотной группе присоединена цепочка из 17 атомов углерода. Можно также рассматривать стеариновую кислоту как относительно длинный углеводород тетрадекан с кислотной группой на конце. В общем, жирная кислота — это длинная углеводородная цепочка с органической кислотной группой на одном из концов. Эта кислотная группа образует водородные связи с водой. Как говорилось в главе 15, уксусная кислота растворима в воде благодаря сильным водородным связям между кислотной группой и молекулами воды. Стеариновая кислота, как и жирные кислоты вообще, нерастворима в воде из-за длинной углеводородной цепочки. Хотя кислотная группа сильно взаимодействует с водой (гидрофильна), длинная углеводородная цепочка, подобно обсуждавшимся в главе 15 углеводородам, избегает взаимодействия с водой (гидрофобна). У жирных кислот влияние длинной углеводородной части молекулы перевешивает, и в общем случае они не растворяются в воде.

Рис. 16.1. Шаростержневая (вверху) и объёмная (внизу) модели стеариновой кислоты. Стеариновая кислота содержит 18 атомов углерода, 36 атомов водорода и два атома кислорода. Это 17-углеродный углеводород с кислотной группой −COOH на конце (справа)

Насыщенные и ненасыщенные жирные кислоты

Стеариновая кислота является насыщенной. Все атомы углерода в ней связаны с одним или двумя другими соседними углеродными атомами одиночной связью. Двойных связей между атомами углерода нет. К насыщенным относят такие жиры, в молекулах которых между атомами углерода есть лишь одиночные связи.

На рис. 16.2 изображена шаростержневая модель олеиновой (масляной) кислоты. Олеиновая кислота, как и стеариновая, содержит 18 атомов углерода и кислотную группу на конце. Однако у неё имеется двойная связь между девятым и десятым атомами углерода (нумерация начинается от атома углерода в составе карбоксильной кислотной группы^{29}). Олеиновая кислота — мононенасыщенная. Она является ненасыщенной, потому что имеет двойную связь, и мононенасыщенной, потому что такая связь только одна. В насыщенных жирах нет двойных связей между атомами углерода.

В стеариновой кислоте все атомы углерода, кроме входящего в кислотную группу, используют для образования связей четыре гибридные sp³-орбитали. Атомы углерода, которые не находятся на концах молекулы стеариновой кислоты, используют две из четырёх гибридных sp³-обиталей для образования одиночных связей с двумя соседними атомами углерода и две другие для связей с атомами водорода.

Все атомы углерода, кроме входящего в кислотный остаток, имеют тетраэдрическую конфигурацию связей с другими атомами углерода и водорода. В олеиновой кислоте девятый и десятый атомы углерода используют три гибридные sp²-орбитали для образования σ-связей — одной с водородом и двух с соседними атомами углерода. Остающиеся 2p-орбитали девятый и десятый атомы углерода используют для образования между собой π-связи. Таким образом, девятый и десятый атомы углерода соединены двойной связью и имеют треугольную, а не тетраэдрическую конфигурацию связей. Это различие в геометрии отчётливо видно на рис. 14.14 при сравнении моделей этана (одиночная углерод-углеродная связь) и этилена (двойная углерод-углеродная связь). В этане углеродные центры тетраэдрические, в этилене — треугольные. Олеиновая кислота содержит 34 атома водорода против 36 в стеариновой кислоте. В олеиновой кислоте для образования двойной связи используются две орбитали, которые в стеариновой кислоте служат для присоединения атомов водорода. Насыщенные жиры содержат максимально возможное число атомов водорода, что означает отсутствие двойных связей.

Рис. 16.2. Шаростержневая модель олеиновой кислоты. Олеиновая кислота содержит 18 атомов углерода подобно стеариновой кислоте на рис. 16.1, но у неё есть одна двойная углерод-углеродная связь между девятым и десятым атомами углерода, считая от кислотной группы

Формы жировых молекул

Стеариновая кислота, изображённая на рис. 16.1, целиком находится в транс-конформации. На рис. 14.13 изображена молекула бутана в транс-конформации, но с поворотом вокруг одной из связей, дающим гош-конформацию. Молекула стеариновой кислоты может принимать множество конформаций, помимо изображённой чистой транс-конформации. Для насыщенных углеводородов и насыщенных жирных кислот чистая транс-конформация является самой прямолинейной и низкоэнергетической. В силу наличия только одиночных углерод-углеродных связей насыщенные жирные кислоты постоянно переходят из одной конформации в другую. На рис. 15.7 изображён гептадеканацетат в конформации, которая не является чистой транс-конформацией.

В отличие от стеариновой кислоты олеиновая кислота (см. рис. 16.2) не может естественным образом находиться в чистой транс-конформации. На рис. 16.2 углы между атомами углерода 8, 9 и 10, а также 9, 10 и 11 составляют 120° (что соответствует треугольнику), а не 109,5° (что характерно для тетраэдра). Таким образом, в нормальных биологических условиях добавление одной двойной связи фиксирует конкретную форму молекулы вблизи этой связи.

Насыщенные, мононенасыщенные и полиненасыщенные жирные кислоты

На рис. 16.3 представлена шаростержневая модель α-линоленовой кислоты. Так же как стеариновая и олеиновая кислоты, α-линоленовая кислота содержит 18 атомов углерода, но она имеет три двойные связи.

Рис. 16.3.Шаростержневая модель α-линоленовой кислоты, которая содержит 18 атомов углерода и имеет три двойные углерод-углеродные связи

В линоленовой кислоте шесть атомов углерода, а именно 9-й, 10-й, 12-й, 13-й, 15-й и 16-й, имеют треугольную конфигурацию с углом 120°, и такие тройки углеродных атомов, как 8-й, 9-й и 10-й, образуют угол 120°, а не тетраэдрический угол 109,5°. В нормальных условиях эти дополнительные двойные связи уводят форму молекулы всё дальше от чистой транс-конфигурации. Хотя α-линоленовая кислота имеет три двойные связи, очень похожая на неё линоленовая кислота имеет только две такие связи. Жирные кислоты без двойных связей называются насыщенными, с одной двойной связью — мононенасыщенными, а с двумя и более двойными связями — полиненасыщенными.

Важность двойных связей в жирных кислотах

Почему так важно, есть ли в жирных кислотах двойные связи? Этот вопрос мы будем рассматривать отдельно для искусственно (химически) модифицированных жиров и натуральных (химически не модифицированных) жиров, содержащихся, например, в сливочном масле и других подобных источниках жира. Начнём с жирных кислот, которые не были химически модифицированы. Известна связь между потреблением жиров и повышением или понижением уровня холестерина. Миристиновая кислота с 14 атомами углерода является насыщенной и, как считается, значительно повышает уровень холестерина, причём вредной для человека его составляющей. Пальмитиновая кислота с 16 атомами углерода тоже насыщенная и в той же мере повышает уровень холестерина. Напротив, линоленовая кислота (18 атомов углерода с двумя двойными связями) и другие полиненасыщенные жирные кислоты понижают уровень холестерина. Однако некоторые насыщенные жирные кислоты, такие как стеариновая (см. рис. 16.1), по-видимому, не оказывают большого влияния на уровень холестерина, что также относится к мононенасыщенным жирным кислотам, таким как олеиновая кислота (см. рис. 16.2).

В обычных пищевых маслах доля важных ненасыщенных и полиненасыщенных жиров сильно варьируется. В сливочном и кокосовом маслах содержится большое количество миристиновой и пальмитиновой кислоты и очень мало линоленовой. Оливковое масло не содержит миристиновой кислоты, но в нём имеется значительное количество пальмитиновой кислоты. В нём также есть линоленовая кислота. В масле канола^{30} совсем нет миристиновой кислоты и почти нет пальмитиновой. В нём имеется значительное количество линоленовой кислоты. Масло из виноградных косточек, сафлоровое и подсолнечное масло (последние два при условии, что они не подвергались высокотемпературной обработке в процессе приготовления пищи, см. ниже) содержит большое количество линоленовой кислоты, немного пальмитиновой и совсем не содержит миристиновой. Химический состав этих жиров свидетельствует о том, что потребление сливочного и кокосового масел оказывает негативное влияние на содержание холестерина в крови (приводит к его повышению), оливковое масло ведёт себя примерно нейтрально, канола оказывает положительное влияние, а масло из виноградных косточек, сафлоровое и подсолнечное (два последних без высокотемпературной обработки) очень благотворно влияют на содержание холестерина в крови.

Химически модифицированные жирные кислоты

Жиры подвергают химической модификации по нескольким причинам. Ненасыщенные жирные кислоты — это молекулы с двойными связями. Двойные связи химически очень активны. Так, в ненасыщенных жирах они могут вступать в реакцию с кислородом. Если этот процесс заходит достаточно далеко, то запах и вкус масла становятся неприятными — масло прогоркает. Скорость реакции ненасыщенных жиров с кислородом резко возрастает под действием света.

Полиненасыщенные жиры имеют много двойных связей. Из-за наличия большего числа двойных связей, готовых к реакции с кислородом, полиненасыщенные масла портятся значительно быстрее. Масла, содержащие ненасыщенные жиры, должны храниться в холодильнике, поскольку снижение температуры замедляет химические реакции, вызывающие прогорклость. Если такое масло нельзя поместить в холодильник, лучше хранить его в тёмном прохладном месте. Некоторые виды масла продаются в бутылках из тёмного стекла. Тёмная бутылка может продлить срок хранения масла на магазинной полке, где оно подвергается воздействию света. Масла, состоящие почти полностью из насыщенных жиров, могут длительное время храниться без охлаждения. Поэтому многие масла химически обрабатываются с целью уменьшить число двойных связей или полностью избавиться от них. Такая обработка может менять физические свойств масел, повышая температуру их плавления и кипения. Эти изменения могут быть полезны при приготовлении пищи, например при выпечке хлеба и в других кулинарных процедурах.

Частично гидрогенизированные и гидрогенизированные жиры

Масла, химически модифицированные с целью уменьшения числа двойных связей или их полного исключения, называются соответственно частично гидрогенизированными или гидрогенизированными. В насыщенных жирных кислотах (не имеющих двойных связей) каждый атом углерода связан с двумя другими атомами углерода и двумя атомами водорода; исключение составляют атомы углерода на концах молекулы. Двойная связь избавляет от двух атомов водорода. Это видно на примере стеариновой кислоты (см. рис. 16.1) и олеиновой кислоты (см. рис. 16.2). Двойные связи между девятым и десятым атомами углерода в олеиновой кислоте используют для каждого из двух атомов углерода, по одной связи из числа тех, что в стеариновой кислоте образуют связи с атомами водорода. Таким образом, процесс избавления жира от двойных связей увеличивает в нём число атомов водорода, и поэтому говорят, что масло гидрогенизируется.

Гидрогенизация жиров

Двойные связи очень устойчивы, и разорвать их трудно. Процесс гидрогенизации превращает двойную углерод-углеродную связь в одиночную, добавляя по одному атому водорода к каждому атому углерода. Для этого процесса необходимы высокая температура, металлический катализатор и водород. Катализатор — вещество, ускоряющее протекание химической реакции, но сам катализатор при этом не расходуется. На качественном уровне процесс гидрогенизации протекает следующим образом. Один из атомов углерода, имеющих двойную связь, связывается с металлом, что, по сути, и уничтожает двойную связь. В результате у другого атома углерода возникает неспаренный электрон. Этот атом углерода теперь имеет одиночные связи с двумя другими атомами углерода и с одним атомом водорода. Как мы уже знаем, атом углерода стремится создать четыре связи, чтобы получить достаточное число электронов для формирования замкнутой конфигурации оболочки неона. Этот атом углерода захватывает атом водорода. Другой атом углерода разрывает связь с катализатором и захватывает ещё один атом водорода. Двойная углерод-углеродная связь превращается в одиночную, а к молекуле жирной кислоты присоединяются два атома водорода.

В полиненасыщенных жирных кислотах этот процесс может повторяться для всех двойных связей или произойти только с одной из них. Если он осуществляется для всех двойных связей, то полиненасыщенная жирная кислота превращается в насыщенную; в этом случае говорят, что происходит гидрогенизация. Если же этот процесс затрагивает лишь некоторые, но не все двойные связи, то говорят о частичной гидрогенизации. Получившаяся жирная кислота может оказаться мононенасыщенной или остаться полиненасыщенной, но с меньшим числом двойных связей. Степенью гидрогенизации управляют для получения жиров с желаемыми свойствами, такими, например, как твёрдое или жидкое состояние при комнатной температуре, требуемые температуры плавления и кипения.

Читайте этикетки

Как отмечалось выше, полиненасыщенные жиры могут быть полезны. В натуральных подсолнечном и сафлоровом маслах содержание полиненасыщенных жиров очень высоко. Однако многие поступающие в продажу сорта этих масел частично гидрогенизированы, что делает их более подходящими для использования при высокотемпературном приготовлении пищи. О том, было ли подсолнечное или сафлоровое масло частично гидрогенизировано, можно судить по данным о пищевой ценности, приводимым на этикетке. Если там сказано, что количество мононенасыщенных жиров больше, чем полиненасыщенных, значит, масло было частично гидрогенизировано. В случае, когда масло не подвергалось гидрогенизации, количество полиненасыщенных жиров в нём значительно превосходит количество мононенасыщенных. Поэтому для получения всей пользы, которую даёт высокое содержание полиненасыщенных жиров в подсолнечном и сафлоровом маслах, такое масло не должно быть частично гидрогенизированным. Чтение этикеток позволит в этом разобраться^{31}.

Транс-жиры

Все эти разговоры о гидрогенизации масла замечательным образом оставляют в стороне главную проблему — транс-жиры. Что это такое? На рис. 16.4 изображена олеиновая кислота в двух конформациях — цис^{32} и транс. Обе молекулы содержат 18 атомов углерода, 34 атома водорода и одну двойную углерод-углеродную связь. Атомы соединены друг с другом в одном и том же порядке. Различия касаются геометрии молекулы вблизи двойной связи.

В цис-конформации два атома водорода, связанные с девятым и десятым атомами углерода, находятся с одной и той же стороны молекулы. Они смотрят под углом в сторону верха страницы. Молекула изображена так, что двойная связь расположена горизонтально. Угол между двойной связью и одним из атомов H составляет 120°, поскольку для образования σ-связей служат треугольные sp²-гибридизированные σ-орбитали. Поэтому направления от девятого и десятого атомов углерода к атомам водорода составляют 30° к вертикали. В цис-молекуле две цепочки атомов, отходящие от девятого и десятого атомов углерода с двух сторон от двойной связи, отклоняются вниз и составляют угол 60° с вертикальной линией, перпендикулярной двойной связи.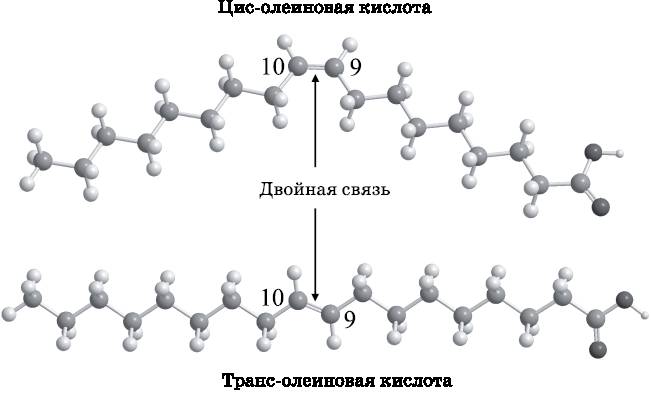

Рис. 16.4. Шаростержневые модели цис-олеиновой и транс-олеиновой кислот. И та и другая содержат 18 атомов углерода и одну двойную связь, однако их геометрия различается

В транс-конформации два атома водорода присоединены к девятому и десятому атомам углерода с противоположных сторон молекулы. Один указывает почти прямо вверх, а другой — почти прямо вниз. Две цепочки углеродных атомов, отходящие от девятого и десятого атомов углерода, идут в противоположных направлениях относительно двойной связи. В итоге цис-молекула «изогнута» в месте двойной связи, тогда как транс-молекула остаётся в этом месте практически «прямой».

В нормальных условиях поворот вокруг углерод-углеродной двойной связи невозможен. Эта невозможность поворота имеет колоссальное значение. На рис. 14.13 изображены гош- и транс-конформации н-бутана, который содержит только одиночные связи. Поворот вокруг одиночной связи легко происходит при комнатной температуре. Поэтому в случае н-бутана гош- и транс-конформациии не зафиксированы. На самом деле, будучи растворены в жидкости при комнатной температуре гош- и транс-конформации н-бутана переходят друг в друга за счёт поворотов вокруг одиночной средней углерод-углеродной связи примерно за 50 пс (50 триллионных долей секунды), то есть за очень короткое время. Напротив, цис- и транс-конформации олеиновой кислоты, изображённые на рис. 16.4, зафиксированы. Они не переходят друг в друга без очень высокой температуры и катализатора.

Чтобы понять, почему поворот вокруг одиночной углерод-углеродной связи происходит легко, а вокруг двойной связи невозможен, надо рассмотреть гибридные орбитали, используемые углеродом для создания одиночной и двойной углерод-углеродной связей. На рис 14.9 изображены гибридные орбитали, служащие в этане для образования одиночной углерод-углеродной связи. Каждый атом углерода связан с другими атомами одной из четырёх гибридных sp³-орбиталей. В средней части рис. 14.9 схематически показано образование углерод-углеродной связи за счёт перекрытия sp³-орбитали одного атома углерода с такой же орбиталью другого. Поворот одного из атомов не влияет на перекрытие орбиталей. Предпочтительная конфигурация образуется благодаря тому, что атомы водорода, присоединённые к двум атомам углерода, стремятся по возможности избегать друг друга, но молекула легко может повернуться и перейти из одной предпочтительной конфигурации в другую без изменения характера перекрытия углерод-углеродной sp³-орбитали. Это резко отличается от ситуации в этилене, где углерод-углеродная связь двойная.

На рис. 14.15 изображены орбитали, служащие для образования двойной связи в этилене. Каждый атом углерода использует три гибридные sp²-орбитали для образования σ-связей с атомами водорода и другим атомом углерода, как показано в верхней части рис. 14.15. Эти три sp²-орбитали у каждого атома углерода образованы суперпозицией 2s-, 2p_x- и 2p_y-орбиталей. Данные орбитали и σ-связи расположены в плоскости страницы, которая принимается за плоскость xy. При этом у каждого атома углерода остаётся одна 2p_z-орбиталь, которая направлена перпендикулярно плоскости страницы. Как показано в нижней части рис. 14.15, две 2p_z-орбитали перекрываются боками и образуют π-связь. Если бы удалось захватить один из атомов углерода и начать поворачивать его, то 2p_z-орбиталь отклонилась бы от оси z в направлении плоскости xy. Такой поворот уменьшил бы перекрытие двух 2p_z-орбиталей, разрушая π-связь. Как показано в таблице, которая приводится вслед за обсуждением рис. 13.9, двойная связь намного сильнее одиночной. Поэтому потребовалась бы очень большая энергия, чтобы выполнить поворот вокруг двойной углерод-углеродной связи, поскольку для этого необходимо разрушить π-связь. Именно этот огромный потенциальный энергетический штраф препятствует повороту.

Природа производит цис-жиры, а химическая обработка — транс-жиры

Ненасыщенные жиры — как мононенасыщенные, так и полиненасыщенные — образуются в природе почти исключительно в цис-конформациях. Небольшое количество транс-жиров обнаружено в мясе и молоке коров, овец, коз и других жвачных животных. Однако огромное количество транс-жиров присутствует в частично гидрогенизированном масле, и, кроме того, транс-жиры обнаружены в гидрогенизированном масле, поскольку химическая обработка не позволяет добиться стопроцентного насыщения жирных кислот. Необработанные мононенасыщенные и полиненасыщенные растительные жиры содержат только цис-конформации в местах двойных связей. Частичная гидрогенизация масла натурального происхождения порождает большое количество транс-жиров. Переход из цис-конформации в транс-конформацию случается во время процесса гидрогенизации.

Как уже отмечалось, соединённые двойными связями атомы углерода, находясь в реакторе при высокой температуре, связываются с металлическим катализатором. Пока сохраняется связь с катализатором, углерод-углеродная связь фактически является одиночной, и могут происходить повороты, переводящие цис-конформацию в транс-конформацию. Атом катализатора может отсоединиться от молекулы жира прежде, чем произойдёт гидрогенизация, и в таком случае двойная связь не гидрогенизируется, но она может поменять конформацию. Если переход из цис-конформации в транс-конформацию случится до того, как молекула освободит катализатор, то результатом будет переход цис-конформации в транс-конформацию без гидрогенизации двойной связи. Обработка, предназначенная для уменьшения числа двойных связей, не устраняет их все. Однако существенное число двойных связей переходит из цис-конформации в транс-конформацию. В результате частично гидрогенизированное масло может содержать значительное количество двойных связей в транс-конформации.

Транс-жиры могут быть опасны

Было продемонстрировано, что транс-жиры оказывают ряд опасных воздействий на здоровье человека. Основная причина вредного влияния транс-жиров связана с тем фактом, что биологические системы приспособлены иметь дело с цис-жирами — форма тут имеет значение. Энзимы — это белки (крупные биологические молекулы), работающие как очень узкоспециализированные химические фабрики. Они могут преобразовывать жиры в другие полезные молекулы, а также расщеплять жиры, чтобы от них избавиться. Однако энзим, который работает с цис-жиром, в общем случае не осуществляет тех же химических реакций с транс-жиром (а может и вовсе не осуществлять никаких реакций), несмотря на идентичность химической формулы. Поэтому две молекулы жирных кислот, содержащие одинаковое число атомов углерода, водорода и кислорода, соединённых между собой в одинаковом порядке, будут на биохимическом уровнеобрабатываться очень по-разному в зависимости от того, находятся они в цис- или транс-конформации. Наш организм не приспособлен иметь дело с большим количеством транс-жиров.

Транс-жиры тесно связаны с развитием сердечно-сосудистых заболеваний, поскольку они влияют на уровень холестерина в крови. Транс-жиры также могут оказывать пагубное воздействие на нервную систему. Миелин — это вещество, образующее защитную оболочку нейронов. Миелин примерно на 30 % состоит из белков и на 70 % — из жирных кислот, две основные из которых — это олеиновая кислота (см. рис. 16.2 и 16.4) и докозагексаеновая кислота (ДГК, см. ниже). Транс-изомеры жирных кислот заменяют ДГК в мембранах клеток мозга и в миелине. Они влияют на электрические сигналы, которые передают сообщения в нервной системе, воздействуя на коммуникации между нейронами. Это удивительно, но изменение формы молекулы без изменения химического состава может превратить полезную пищу во вредную.

Когда ноль — это ноль

Многочисленные примеры вредного влияния транс-жиров на здоровье человека свидетельствуют о том, что употребления их следует избегать. Общества по защите прав потребителей агитируют за обязательное удаление транс-жиров из пищевых масел, используемых в ресторанах быстрого питания и в различных продуктах пищевой промышленности. Из-за большого количества негативной информации о транс-жирах производители стараются скрыть их наличие в продуктах питания от потребителей. Сегодня, когда большинство людей знает, что частичная гидрогенизация порождает транс-жиры, в описание жиров на некоторых марках продуктов стали использовать термин «модифицированные» вместо «частично гидрогенизированные». Ещё большее недоумение вызывает принятое правительством США определение «0 % транс-жиров». Нормативные документы разрешают производителям сообщать, что масло содержит 0 % транс-жиров, если одна порция содержит меньше чем 0,5 грамма транс-жиров, но производителям позволено самим определять размер порции. Допустим, что в столовой ложке масла содержится 0,6 грамма транс-жиров. Одна столовая ложка — это три чайные ложки. Производитель может определить порцию как две чайные ложки, в которых содержится 0,4 грамма транс-жиров. В результате за счёт подгонки определения порции оказывается, что масло содержит 0 % транс-жиров. Такого рода манипуляции с маркировкой не допускаются в странах Западной Европы и ряде других стран. Минимизируя потребление частично гидрогенизированных масел, вы уменьшаете вредное воздействие транс-жиров на своё здоровье.

Омега−3 жирные кислоты

На рис. 16.5 изображена шаростержневая модель докозагексаеновой кислоты (ДГК). Как уже упоминалось, ДГК является важной составляющей покрытия нервных волокон. Она содержит 22 атома углерода и шесть двойных углерод-углеродных связей. Она сильно ненасыщенная. Все её двойные связи находятся в цис-конфигурации. ДГК относится к классу ненасыщенных жирных кислот, широко известных как омега−3 (ω−3). Эти жирные кислоты считаются очень полезными для здоровья^{33}.

Более правильно называть этот класс жиров n−3 жирными кислотами, где n — число атомов углерода. Атомы углерода нумеруются, начиная с того, который входит в состав карбоновой кислоты и имеет номер 1. Тогда, если пройтись по всей цепочке ДГК, последний атом углерода на конце, противоположном группе карбоновой кислоты, будет иметь номер 22 (см. рис. 16.5). Это и есть n — число атомов углерода в цепочке. Углерод n−3 имеет номер на 3 меньше, чем у последнего атома углерода в цепочке. Для ДГК этот номер равен 19, что и отмечено на рис. 16.5. Жирная кислота относится к классу ω−3, если «эн-минус-третий» атом углерода связан двойной связью, как это показано на рисунке. Изображённая на рис. 16.3 α-линоленовая кислота тоже является ω−3 жирной кислотой. Она содержит 18 атомов углерода, так что n−3=15. Как видно из рис. 16.3, имеется двойная связь между 15-м и 16-м атомами углерода.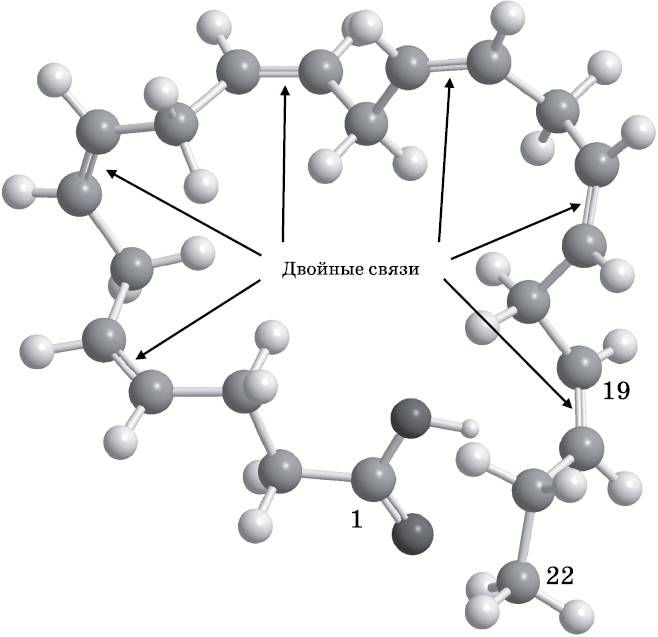

Рис. 16.5. Шаростержневая модель докозагексаеновой кислоты (ДГК). ДГК — это полиненасыщенные жиры с двадцатью двумя атомами углерода и шестью двойными углерод-углеродными связями, находящимися в цис-конформации

Триглицериды

Жирные кислоты, обсуждавшиеся до сих пор, содержат одну цепочку. Однако жиры, содержащиеся в живых организмах, содержат три молекулы жирных кислот, связанные в одну молекулу. Их называют триглицеридами. Каприновая кислота — это насыщенная жирная кислота с десятью атомами углерода. Триглицерид каприновой кислоты изображён на рис. 16.6.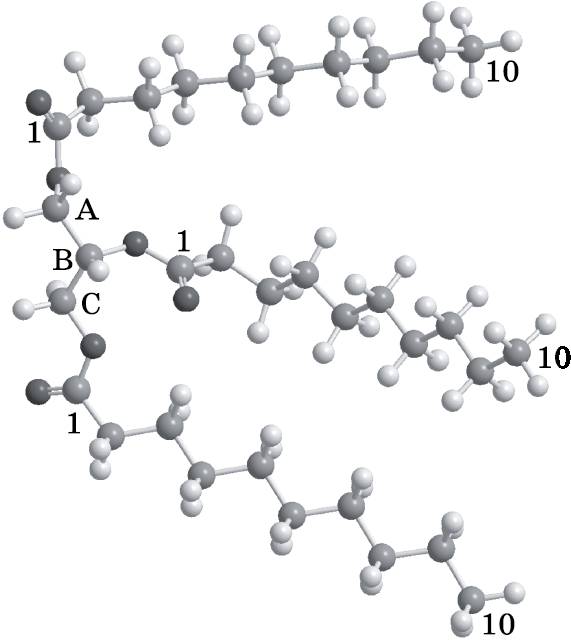

Рис. 16.6. Шаростержневая модель триглицерида каприновой кислоты, которая состоит из трёх цепочек каприновой кислоты. Каждая цепочка является насыщенной жирной кислотой с десятью атомами углерода (на рисунке помечены крайние — 1-е и 10-е атомы). Они присоединены к трём атомам углерода, обозначенным A, B и C

В него входят три цепочки каприновой кислоты, первый атом каждой из которых помечен 1, а последний — 10, а также короткая цепочка из трёх атомов углерода, обозначенных A, B и C. В свободном состоянии каприновой кислоты атом углерода, принадлежащий группе карбоновой кислоты (помеченный 1) соединён двойной связью с одним атомом углерода и одиночной связью с гидроксильной группой −OH. В триглицериде атом H гидроксильной группы заменяется одним из атомов углерода трёхуглеродной цепочки. На рис. 16.6 верхняя цепочка связана с атомом углерода A, средняя цепочка — с атомом углерода B, а нижняя — с атомом углерода C. Триглицерид каприновой кислоты относится к классу среднецепочечных триглицеридов. Среднецепочечные триглицериды (СЦТ) содержат цепочки длиной от 6 до 12 атомов углерода. Длинноцепочечные триглицериды (ДЦТ) содержат цепочки длиной более 12 атомов углерода.

Холестерин

В разговорах о питании и жирах часто приходится слышать, что не стоит потреблять слишком много жирной пищи, поскольку это повышает уровень холестерина. Отсюда у многих людей складывается ошибочное впечатление, будто холестерин является жиром. Они думают, что поедание большого количества жира означает поедание большого количества холестерина. Однако холестерин не является жиром. В действительности это спирт, на что указывает суффикс «-ол» в его более корректном химическом названии — холестерол^{34}. Этот суффикс используется для указания на то, что молекула является спиртом, как, например, этанол (см. рис. 15.1). Строение холестерина показано на рис. 16.7. Вверху изображена схема холестерина, посередине — его шаростержневая модель, а внизу — объёмная модель. Спиртовая OH-группа находится на диаграмме слева, а на шаростержневой и объёмной моделях — слева внизу. Молекула содержит четыре углеродных кольца, пронумерованных от 1 до 4. На рисунке во всех узлах находятся атомы углерода, и каждый из них имеет четыре связи. Атомы водорода не показаны, за исключением тех мест, где необходимо отметить, расположен атом водорода перед плоскостью страницы или за ней. Если на конце треугольника нет символа H, значит, там находится метильная группа −CH₃.

Рис. 16.7. Холестерин. Вверху: схема молекулы холестерина. Посередине: шаростержневая модель. Внизу: объёмная модель. Холестерин — это спирт (с OH-группой), состоящий из четырёх углеродных колец, пронумерованных от 1 до 4, и углеродной цепочки

Схема в верхней части рисунка позволяет увидеть, как атомы соединены друг с другом. Шаростержневая модель даёт более подробную трёхмерную иллюстрацию строения молекулы. Объёмная модель реалистичнее представляет картину трёхмерного строения молекулы. Она охватывает области пространства, где концентрируется большая часть распределения вероятности для электронов. Важно помнить, что молекулы — это не стержни и шары, а делокализованные электронные облака, окружающие положительно заряженные ядра, которые находятся в центрах атомов.

Если сравнить строение холестерина на рис. 16.7 с любыми моделями жирных кислот, представленными выше, становится очевидно, что холестерин совсем на них не похож. Например, объёмная модель стеариновой кислоты (см. рис. 16.1) сильно отличается от объёмной модели холестерина на рис. 16.7. Ясно, что на молекулярном уровне холестерин имеет мало общего с жирными кислотами. Тем не менее он часто обсуждается в связи с жирами, содержащимися в пище, а сама молекула холестерина приобрела крайне негативную «ауру».

Вопреки общему мнению, холестерин полезен

Да, холестерин пользуется дурной славой. Тем не менее это чрезвычайно важная биологическая молекула. Клетки окружены мембранами. Внутри клетки располагаются все те сложные молекулярные машины, которые необходимы для осуществления химических процессов, ответственных за жизнедеятельность. Вне клетки находится множество других химических соединений, включая кислород, соли и крупные биологические молекулы. Клеточная мембрана отделяет внутреннюю часть клетки от внешнего пространства, позволяя некоторым молекулам проходить внутрь и наружу, тогда как другие всегда остаются снаружи или внутри. Важнейшим компонентом клеточной мембраны являются фосфолипиды. Фосфолипиды состоят из двух углеводородных цепочек длиной обычно по 16 атомов углерода, присоединённых одним концом к головной группе, которая несёт положительный и отрицательные заряды. Эти заряды делают головную группу чрезвычайно гидрофильной (притягивающейся к воде). Углеводородные цепочки крайне гидрофобны (отталкиваются от воды). Клетки окружены водой и содержат много воды внутри. Заряженные головные группы стремятся быть в воде, тогда как углеводородные хвосты избегают воды. Чтобы одновременно удовлетворить требованиям заряженных гидрофильных головных групп и гидрофобных углеводородных хвостов, фосфолипиды организуются в двуслойную структуру, схематически изображённую на рис. 16.8.

Рис. 16.8. Схематическое изображение участка двойного фосфолипидного слоя с двумя молекулами холестерина. Головные группы (шары) заряжены и стремятся к воде. Углеводородные хвосты избегают воды, образуя двойной слой. Гидроксильная группа холестерина находится у границы воды

На рисунке показано сечение двуслойной фосфолипидной мембраны, которая полностью окружает и ограничивает клетку. Здесь шары — это заряженные головные группы, а волнистыми линиями представлены углеводородные цепочки. Реальная клеточная мембрана намного сложнее, чем показано на рис. 16.8. Она содержит множество белков, выполняющих специфические функции, такие как пропуск определённых ионов или молекул внутрь клетки и воспрепятствование прохождению других.

Помимо фосфолипидов, основной составляющей клеточной мембраны является холестерин. На него приходится около 30 % клеточной мембраны. На рис. 16.8 схематически представлены две молекулы холестерина, замещающие два фосфолипида. Холестерин важен, поскольку он управляет механическими свойствами двойного слоя. Без холестерина клеточная мембрана не могла бы функционировать. Поэтому холестерин крайне важен. Человеческий организм вырабатывает значительное количество холестерина, и лишь небольшая часть необходимого холестерина поступает с пищей. Короче говоря, если вы удалите из своего тела весь холестерин, то умрёте.

Проблема с холестерином

Проблема с холестерином состоит не в том, что вы получаете некоторое его количество с пищей, а в том, как он ведёт себя в организме. Вредное влияние холестерина на здоровье связано с жирами, но не потому что холестерин является жиром, и даже не потому, что жирная пища может содержать холестерин. Холестерин переносится в потоке крови, будучи связанным с очень крупными биомолекулярными комплексами, которые называются липопротеинами. Они состоят из очень крупных белков, фосфолипидов, жирных кислот, холестерина и других молекул. Липопротеины можно разделить по крайней мере на два класса: липопротеины низкой плотности (ЛПНП) и липопротеины высокой плотности (ЛПВП). Они имеют яйцеобразную форму и диаметр около 200 Å (200∙10⁻¹⁰ м). Объём этих частиц составляет около 5000000 ų. Для сравнения: объём молекулы холестерина — примерно 200 ų. Таким образом, частицы ЛПНП и ЛПВП где-то в 20000 раз больше молекулы холестерина и переносят в потоке крови сразу много молекул холестерина. Высокий уровень ЛПНП по отношению к ЛПВП сильно коррелирует с ишемической болезнью сердца и атеросклерозом. Механизм этой связи пока не вполне ясен, но переносящие холестерин ЛПНП приводят к возникновению опасных отложений на стенках артерий, а ЛПВП — нет. Высокий уровень ЛПНП по сравнению с ЛПВП (большое значение отношения ЛПНП к ЛПВП) обусловлен потреблением насыщенных жиров и в ещё большей степени транс-жиров. Транс-жиры не только повышают уровень ЛПНП, но ещё и снижают уровень ЛПВП, усугубляя проблему. Таким образом, потребление жирной пищи имеет значение, но не потому, что она содержит холестерин. Что действительно важно, так это характер употребляемых с пищей жиров. Лучше использовать масла, содержащие большое количество полиненасыщенных жиров, которые не подвергались обработке, порождающей значительное количество транс-жиров.

В главе 14 мы обсуждали одиночные и двойные углеродные связи. Были описаны разные типы гибридных атомных орбиталей, служащих для образования молекулярных орбиталей. Квантовая теория позволяет во всех деталях объяснить химические связи и то, как их природа влияет на форму молекул и силу связей, удерживающих атомы вместе. В этой главе мы на примере жиров проиллюстрировали тот факт, что незначительные, казалось бы, особенности молекулярных связей — одиночные они или двойные, сколько имеется двойных связей, находятся ли они в цис- или транс-конформации — играют в биологии чрезвычайно важную роль. Геометрия двойных связей может быть в буквальном смысле вопросом жизни и смерти.

17. Парниковые газы

В этой главе мы рассмотрим, что происходит, когда уголь, нефть или природный газ сжигают на электростанциях для выработки энергии. Прежде всего, выясним, почему при сжигании угля образуется намного больше парникового углекислого газа, чем при сжигании нефти, которая, в свою очередь, даёт его в расчёте на единицу энергии больше, чем природный газ. Кроме того, углекислый газ столь сильно влияет на парниковый эффект по причине, связанной с фундаментальной квантовомеханической природой черноте́льного излучения и квантованием энергетических уровней.

Углекислый газ, образующийся при сжигании ископаемого топлива

В главе 15 обсуждалось превращение вина (этанола) в уксус (уксусную кислоту) в результате добавления кислорода к молекулам этанола. Когда это происходит, мы говорим, что этанол окисляется до уксусной кислоты. Окисление — химический процесс, который может принимать различные формы, но в случае превращения этанола в уксусную кислоту — это просто добавление кислорода. Процесс ускоряется биологическими энзимами. Углеводороды, например метан и вещества, входящие в состав мазута, тоже могут окисляться. Однако молекулы углеводородов очень устойчивы — они окисляются только при высокой температуре. Горение углеводородного топлива — это и есть процесс окисления. Для его протекания требуется тепло, но когда окисление началось, разрушение химических связей и образование новых молекул высвобождает дополнительное тепло (тепловую энергию), что делает процесс самоподдерживающимся.

Горение метана: природный газ

Рассмотрим сначала, что происходит, когда горит метан (природный газ). Модель молекулы метана изображена на рис. 14.1. Метан CH₄ реагирует с кислородом с образованием воды H₂O и углекислого газа CO₂. Эту реакцию можно записать следующим образом:

CH₄ + 2O₂ → 2H₂O + CO₂.

Данное химическое уравнение показывает, что одна молекула метана реагирует с двумя молекулами кислорода, в результате чего образуются две молекулы воды и одна молекула углекислого газа. Стрелка направлена от реагентов к продуктам реакции. Про такое уравнение говорят, что оно сбалансировано, поскольку число атомов углерода, водорода и кислорода одинаково в левой и правой его частях. В химических реакциях комбинации атомов, составляющих молекулы, меняются, но число атомов каждого типа всегда остаётся неизменным. Кроме того, эта реакция порождает ещё и тепло. Энергия расходуется на разрушение C−H-связей в метане. Однако когда образуются связи O−H и C−O, энергия высвобождается. При образовании связей в молекулах воды и углекислого газа выделяется больше полезной энергии (называемой также свободной энергией), чем затрачивается на разрушение связей в метане. В результате горения метана высвобождается энергия, которая может, например, вскипятить воду для спагетти или крутить паровую турбину для выработки электричества.

Что такое парниковый газ?

Метан — очень хорошее топливо, но при его горении образуется парниковый газ CO₂. Что такое парниковый газ? Обычный парник, где выращивают цветы и помидоры, — это строение, которое пропускает внутрь большое количество солнечного света. Сегодня парники сооружают, покрывая большие площади пластиком, проницаемым для солнечного света, так что он свободно проходит внутрь. Падающее на предметы внутри парника солнечное излучение большей частью ими поглощается и превращается в тепло. Вы, вероятно, знакомы с этим эффектом, если вам доводилось садиться в машину с тёмными сиденьями, на которые долго светило солнце через лобовое стекло. Сиденья становятся очень горячими, а чёрное рулевое колесо может нагреться настолько, что до него будет не дотронуться.

Как говорилось при обсуждении рис. 9.1, горячие предметы испускают черноте́льное излучение, которое охватывает широкий диапазон цветов. Чем горячее предмет, тем выше частота света. Солнце очень горячее и даёт большое количество видимого света (см. рис. 9.1). Нагретое солнцем чёрное автомобильное сиденье не очень горячее и испускает низкочастотное (длинноволновое) черноте́льное излучение. Это длинноволновое излучение приходится на инфракрасную часть электромагнитного спектра. Оно гораздо менее энергично, чем видимый свет. В парнике солнечный свет нагревает находящиеся внутри предметы, но энергия, которая испускается ими в виде инфракрасного черноте́льного излучения, не может пройти сквозь пластик или стекло. Эти материалы прозрачны для видимого света, но не для инфракрасного. Таким образом, солнечная энергия захватывается в ловушку внутри парника, где становится значительно теплее, чем снаружи.

Углекислый газ (а также водяной пар и некоторые другие газы) заставляет атмосферу вести себя подобно парнику для всей нашей планеты. Солнечное излучение приносит на поверхность Земли огромное количество энергии. Земная поверхность нагревается, и часть энергии испускается ею в виде инфракрасного черноте́льного излучения. Атмосфера в основном состоит из газообразных кислорода O₂ и азота N₂. Эти газы прозрачны как в видимой, так и в инфракрасной частях спектра. Если бы атмосфера состояла только из кислорода и азота, всё черноте́льное излучение нагретой поверхности Земли свободно уходило бы в космос. Земля была бы намного холоднее, чем она есть, и, вероятно, не подходила бы для жизни человека. Однако атмосфера содержит и другие газы. В ней примерно 78 % азота, 21 % кислорода, 0,9 % аргона и 0,038 % углекислого газа. Кроме того, в ней присутствуют следы других газов и водяной пар, количество которого постоянно изменяется. Концентрация CO₂ в воздухе очень мала, но этот газ чрезвычайно важен. Углекислый газ прозрачен для видимого света, но поглощает инфракрасное излучение. (Ниже мы обсудим, почему углекислый газ поглощает свет в инфракрасном диапазоне, что делает его важным парниковым газом.) Таким образом, CO₂ позволяет солнечному свету падать на земную поверхность, но поглощает часть инфракрасного черноте́льного излучения, мешая ему уходить в космос.

Значительная часть инфракрасного черноте́льного излучения всё же уходит в космос. Однако баланс здесь очень тонкий. Солнечный свет нагревает Землю. Уходящее в космос черноте́льное инфракрасное излучение охлаждает её. Поглощение инфракрасного излучения содержащимся в воздухе углекислым газом ослабляет этот охлаждающий эффект. При недостаточном содержании CO₂ в воздухе слишком много энергии будет уходить в космос и на Земле станет слишком холодно, а при избыточном содержании CO₂ в космос будет излучаться недостаточно тепла и на Земле станет слишком жарко. CO₂ действует подобно стеклянным или пластиковым окнам настоящего парника. Он удерживает тепло внутри, в данном случае внутри атмосферы^{35}.

На настоящий момент содержание CO₂ в воздухе составляет 0,038 %, или 380 ppm^{36}. В 2000 году оно составляло 368 ppm, в 1990 году — 354 ppm, в 1980 году — 336 ppm, в 1970 году — 325 ppm, в 1960 году — 316 ppm. Эти данные получены по измерениям в обсерватории Мауна-Лоа, Гавайи, США. Анализ воздушных включений антарктического льда позволил определить, что в 1832 году концентрация CO₂ в воздухе составляла 284 ppm. Систематическое изменение концентрации CO₂ очевидно, и в большом числе научных работ было убедительно продемонстрировано, что рост содержания CO₂ в атмосфере связан с деятельностью человека. Основной вклад в прирост содержания CO₂ в воздухе даёт сжигание ископаемого топлива, хотя и другие виды деятельности, такие как вырубание тропических лесов, также вносят свою лепту. Что случится, если концентрация CO₂ в атмосфере продолжит расти? Экстремальным примером реализации такого сценария может служить Венера. Её атмосфера более чем на 90 % состоит из CO₂, а температура на её поверхности составляет 480 °C.

При сжигании ископаемого топлива выделяется углекислый газ

Из уравнения, описывающего горение метана (реакцию метана с кислородом), видно, что в результате образуется CO₂. Это происходит и при горении других видов ископаемого топлива. Как уже говорилось, мазут представляет собой смесь длинноцепочечных углеводородов, содержащих от 14 до 20 атомов углерода. Мы рассмотрим в качестве примера молекулу тетрадекана, содержащую 14 атомов углерода. Вот химическое уравнение горения тетрадекана:

C₁₄H₃₀ + 21,5O₂ → 14CO₂ + 15H₂O.

Тетрадекан содержит 30 атомов H, которые дают 15 молекул воды, каждая из которых содержит по два атома. В неё также входит 14 атомов C, которые превращаются в 14 молекул углекислого газа. На образование 14 молекул CO₂ и 15 молекул H₂O требуется 43 атома кислорода или 21,5 молекулы O₂. Вот почему в левой части химического уравнения перед O₂ стоит коэффициент 21,5. Обратите внимание, что химическое уравнение горения метана даёт вдвое больше молекул воды, чем молекул углекислого газа. При горении тетрадекана образуется примерно одинаковое количество молекул воды и углекислого газа. И это имеет большое значение.

Помимо природного газа метана и нефти (длинноцепочечных углеводородов), третьим по распространённости видом топлива является уголь. В первом приближении уголь можно считать чистым углеродом. Это не совсем так, но сейчас нас устраивает такая точность. В таком случае химическое уравнение горения угля имеет следующий вид:

C + O₂ → CO₂.

Таким образом, в отличие от горения углеводородов при сжигании угля не образуется вода, а выделяется только CO₂. При сжигании углеводородов углерод-углеродные и углерод-водородные связи должны разрушаться, на что затрачивается энергия. Затем при образовании углекислого газа и воды формируются углерод-кислородные и кислород-водородные связи, и это происходит с выделением энергии. В угле тоже есть связи, которые должны быть разрушены. Это углерод-углеродные связи. Для начала мы будем рассматривать уголь как графит, который является чистым углеродом. Нам надо сравнить количество энергии, выделяемой при горении каждого типа ископаемого топлива, с количеством образующегося при этом парникового газа CO₂. Хотя графит не используется в качестве топлива, поскольку его трудно воспламенить, он является удобной моделью благодаря чётко определённому химическому строению.

Выделяемая энергия и количество углекислого газа

Для начала рассмотрим идеализированную картину выделения энергии при сжигании ископаемого топлива. Будем игнорировать тот факт, что топливо содержит примеси и что на электростанциях теряется значительная часть выделяемой энергии — фактическую её выработку при сжигании реального топлива мы обсудим позже. Итак, три химических уравнения горения ископаемых видов топлива:

CH₄ + 2O₂ → 2H₂O + CO₂,

C₁₄H₃₀ + 21,5O₂ → 15H₂O + 14CO₂,

C + O₂ → CO₂.

В первом и третьем уравнениях (горение природного газа и угля) в реакции образуется одна молекула CO₂. Для нашей модели мазута (представленного тетрадеканом) получается 14 молекул CO₂. Мы хотим найти количество энергии, выделяемой в расчёте на одну молекулу CO₂. Методами термодинамики можно рассчитать максимальное количество полезной (свободной) энергии, выделяемой в каждой из реакций. Пусть все эти реакции начинаются при комнатной температуре, когда метан является газом, тетрадекан — жидкостью, а графит — твёрдым веществом. Конечно, продукты горения топлива первоначально оказываются горячими, но мы будем рассматривать ситуацию после того, как всё остыло до комнатной температуры. Для природного газа мы просто используем свободную энергию, выделяющуюся при сгорании одной молекулы; для графита возьмём энергию, выделяемую при сгорании одного атома углерода. В случае тетрадекана мы разделим на 14 энергию, получаемую при сгорании одной молекулы тетрадекана, чтобы получить энерговыделение в расчёте на одну полученную молекулу углекислого газа.

В результате получим следующие значения свободной энергии на одну молекулу CO₂:

метан (природный газ): 1,4∙10⁻¹⁸ Дж;

тетрадекан (мазут): 1,1∙10⁻¹⁸ Дж;

графит (уголь): 0,7∙10⁻¹⁸ Дж.

Как видим, при получении одного и того же количества энергии уголь выделяет в 2 раза больше парникового углекислого газа, чем природный газ. Уголь также в 1,6 раза хуже мазута по выделению углекислого газа в расчёте на единицу энергии, а мазут в 1,3 раза уступает природному газу.

Сжигание реального ископаемого топлива

Приведённые цифры достаточно точны, за исключением той, что дана для угля. Различные типы угля — антрацит, битуминозный, суббитуминозный и бурый — дают разное количество энергии на единицу массы и имеют разное среднее содержание углерода. Даже для одного и того же типа угля энергетические характеристики могут существенно варьироваться. Например, содержание углерода в битуминозном угле, наиболее широко распространённом в США, лежит в диапазоне от 45 до 86 %, а его теплота сгорания варьируется примерно на ±20 % от среднего значения. Значение, подсчитанное выше для угля с использованием графита в качестве модели, даёт результат, соответствующий среднему значению энергосодержания битуминозных углей. Природный газ может, помимо метана (CH₄), содержать до 20 % газообразных углеводородов — этана (C₂H₆), пропана (C₃H₈) и бутана (C₄H₁₀). Эти примеси почти не влияют на значения энергосодержания и выделения энергии в расчёте на одну молекулу CO₂, подсчитанные для чистого метана. То же самое можно сказать и про мазут, который является смесью длинноцепочечных жидких углеводородов.

Реальное количество углекислого газа, выделяемого при производстве электричества

Энергосодержание ископаемых видов топлива не принимает в расчёт эффективность электростанции, то есть КПД преобразования энергии топлива в электричество. Эффективность электростанций зависит от их конструкции и возраста, но примерно одинакова для разных типов ископаемого топлива. Обычно эта эффективность лежит в диапазоне 35–40 %. Это означает, что лишь около 40 % энергии топлива превращается в электроэнергию. Кроме того, потери энергии в линиях электропередачи составляют около 7 %. Так что если электростанция имеет КПД 38 %, то с учётом потерь в линиях электропередачи общий коэффициент преобразования энергии ископаемого топлива в полезное электричество в наших домах составит около 35 %.

Для понимания значения этих цифр давайте подсчитаем, сколько CO₂ образуется при выработке энергии для питания 100-ваттной лампы накаливания, горящей 24 часа в сутки в течение года. Ватт — это Дж/сек (джоуль в секунду), год — это 3,2∙10⁷ секунд. Таким образом, 100-ваттная лампа потребляет 3,2∙10⁹ Дж в год. Природный газ, как было сказано, даёт одну молекулу CO₂ на каждые 1,4∙10⁻¹⁸ Дж выделившейся химической энергии. Чтобы получить 3,2∙10⁹ Дж энергии, нам понадобится произвести 3,2∙10⁹/1,4∙10⁻¹⁸=2,3∙10²⁷ молекул CO₂. Это количество соответствует идеальной эффективности. С учётом общего КПД 35 % получается, что будет произведено 6,4∙10²⁷ молекул CO₂. Масса 6,02∙10²³ молекул CO₂ составляет 44 грамма. Таким образом, будет произведено 5∙10⁵ г CO₂, или примерно полтонны.

Итак, круглогодичное горение 100-ваттной лампочки приводит к выбросу в атмосферу 500 кг CO₂ при использовании природного газа. При сжигании угля будет выброшена тысяча килограммов, то есть одна тонна. Это вес небольшого автомобиля. Таким образом, первый вывод: выключайте свет, когда вы его не используете. Компьютер, который вы оставляете включённым 24 часа 7 дней в неделю, потребляет от 200 до 300 ватт электричества. Это означает, что если вы получаете энергию от угольной электростанции, ваш компьютер приводит к выбросу в атмосферу от двух до трёх тонн CO₂ каждый год. Второй вывод состоит в большом значении эффективности электроприборов и выбора ископаемого топлива. Компактная флуоресцентная лампа, дающая столько же света, сколько обычная 100-ваттная лампа накаливания, потребляет лишь 25 ватт. Поэтому такая энергосберегающая лампа, работающая круглый год от электростанции на газовом топливе, приводит к выбросу 125 кг CO₂ против тонны CO₂ в случае с обычной лампой, питаемой от угольной электростанции.

Углекислый газ является парниковым в силу квантовых эффектов

Почему углекислый газ создаёт столь серьёзную парниковую проблему? Другими словами, почему он удерживает тепло в атмосфере? И почему водяной пар (молекулы воды в газообразной фазе, находящиеся в атмосфере) является ещё более серьёзным парниковым газом, чем CO₂? Содержание в атмосфере водяного пара определяется испарением и конденсацией воды. Земные океаны представляют собой огромный резервуар воды, из которого она испаряется в атмосферу. С дождями, росой и снегом вода покидает воздух. Человек мало влияет на количество находящейся в воздухе воды, однако если Земля продолжит нагреваться, насыщенность атмосферы водяным паром возрастёт. Это ещё более усугубит парниковый эффект, связанный с выбросами CO₂, поскольку H₂O — это очень мощный парниковый газ. Мы, однако, можем влиять на количество CO₂ в атмосфере, выбирая источники энергии и повышая эффективность их использования. Серьёзная роль CO₂ и водяного пара как парниковых газов напрямую вытекает из квантовой теории.

Черноте́льный спектр Земли

В главах 4 и 9 мы обсуждали черноте́льное излучение. На рис. 9.1 изображён черноте́льный спектр Солнца, температура поверхности которого составляет чуть менее 6000 °C. Такое чёрное тело излучает значительную часть энергии в видимой области спектра, а также существенное её количество в ультрафиолетовом и инфракрасном диапазонах. Цвет испускаемого горячим предметом излучения зависит от его температуры. Горячие объекты испускают более короткие волны. Земля, конечно, намного холоднее Солнца. Тем не менее и она является черноте́льным излучателем, но испускает гораздо более длинные волны (менее энергичные фотоны). Солнечный свет со спектром, изображённым на рис. 9.1, падает на Землю. Часть этого света отражается обратно в космос льдом и другими светлыми объектами на поверхности. Однако значительная часть световой энергии превращается в тепло, согревающее Землю. Черноте́льное излучение Земли уносит в космос часть поступающей от Солнца энергии^{37}.

В верхней части рис. 17.1 изображены три расчётных черноте́льных спектра Земли для трёх температур. Эти три кривые нормализованы так, чтобы в максимуме все они имели значение 1. 15 °C — это средняя температура поверхности Земли, 27 °C — температура поверхности в тропиках, а −16 °C — в субарктических регионах. Хотя кривые немного различаются, в целом они очень похожи. При обсуждении роли углекислого газа эти различия несущественны.

Рис. 17.1. Вверху: расчётные черноте́льные спектры Земли для трёх температур (сплошные кривые). Выделенные области соответствуют участкам спектра, в которых происходит сильное поглощение содержащимися в атмосфере водяным паром и углекислым газом. Посередине и внизу: спектры сильного поглощения углекислым газом и водяным паром в диапазоне от 0 до 1000 см ⁻¹ . Обратите внимание, что здесь шкала отличается от использованной на верхнем графике

Поглощение земного черноте́льного излучения

Нижние два спектра на рис. 17.1 (обратите внимание, что шкала отличается от шкалы верхнего спектра) показывают влияние углекислого газа и водяного пара на пропускание атмосферой инфракрасного излучения в длинноволновой части спектра. Пропускание, равное единице, означает, что весь свет проходит сквозь атмосферу. Нулевое пропускание означает, что свет полностью поглощается в атмосфере. Эти спектры меняются в зависимости от региона Земли, где они измеряются. Приведённые кривые дают о них лишь общее представление. Кроме того, на них опущена сложная тонкая структура (пики и впадины), особенно в спектре водяного пара. Смысл этих кривых в том, чтобы показать наиболее существенные особенности поглощения инфракрасного излучения углекислым газом и водяным паром в области, на которую приходится основная часть земного черноте́льного спектра. Эти области поглощения показаны тоном и штриховкой на верхнем графике. Водяной пар также вызывает значительное поглощение в районе 1750 см⁻¹; эта область тоже отмечена. Инфракрасное поглощение мешает части земного черноте́льного излучения уходить в космос. Без этого атмосферного поглощения Земля была бы намного холоднее.

Почему углекислый газ так важен?

Причину, по которой углекислый газ настолько важен, можно понять, присмотревшись к выделенному тоном участку черноте́льного спектра и спектру поглощения. Водяной пар поглощает практически всё более длинноволновое излучение, чем 500 см⁻¹. Однако два нижних спектра на рис. 17.1 показывают, что углекислый газ поглощает излучение как раз в той области, где водяное поглощение незначительно. Полоса поглощения углекислого газа лежит очень близко к пику спектра земного черноте́льного излучения, и, как видно на верхнем графике рис. 17.1, это не зависит от того, какова температура земной поверхности. Таким образом, углекислый газ вызывает сильное поглощение земного черноте́льного излучения в важном спектральном диапазоне, где другие составляющие атмосферы, в частности водяной пар, не проявляются. На спектре поглощения углекислого газа (средний график на рис. 17.1) видно, что в середине полосы поглощения вокруг частоты 667 см⁻¹ пропускание близко к нулю. Однако с увеличением концентрации CO₂ область очень сильного поглощения становится шире, а в части спектра, где пропускается лишь несколько процентов, излучение вовсе перестаёт уходить с Земли в космос. Итак, CO₂ вызывает сильное поглощение вблизи пика земного черноте́льного излучения, где у водяного пара нет такого эффекта, а с ростом концентрации CO₂ атмосфера будет удерживать в ловушке больше черноте́льного излучения, вызывая нагрев планеты.

Почему углекислый газ поглощает именно в этой области?

Мы видим, что углекислый газ захватывает инфракрасное излучение вблизи пика земного черноте́льного излучения и что увеличение концентрации CO₂ пагубным образом сказывается на температуре Земли. Но почему CO₂ поглощает инфракрасное излучение именно вблизи частоты 667 см⁻¹? В главах с 8-й по 11-ю мы обсуждали энергетические уровни частицы в ящике, атома водорода и всех остальных атомов. В главах с 12-й по 14-ю мы обсуждали молекулярные орбитали и связанные с ними энергетические уровни. Весь этот разговор вращался вокруг энергетических уровней для электронов. На основе представления о молекулярных орбиталях объяснялась природа химических связей, которые удерживают вместе атомы в молекулах. Однако мы не говорили о движениях атомов, которые соединены химическими связями в молекулы.

На рис. 12.1 изображена кривая потенциальной энергии для молекулы водорода H₂. Эта кривая показывает, что энергия меняется в зависимости от расстояния между двумя ядрами атомов водорода. Длина химической связи — это расстояние, на котором энергия достигает минимума. Однако эта связь не является жёсткой. Если думать о ней в терминах классической механики, то связь — это пружина с двумя грузами — атомами водорода, присоединёнными к её концам. Пружина может растягиваться и сжиматься. В классической системе, если растянуть пружину и отпустить её, грузы начинают колебаться, вызывая попеременное растяжение и сжатие пружины. В случае классического осциллятора грузы будут колебаться вперёд-назад по хорошо определённой траектории. Опираясь на квантовую теорию, мы сразу должны заподозрить, что у квантовых колебаний не может быть такой хорошо определённой траектории, иначе это означало бы, что мы точно знаем и положение, и импульс частиц (атомов). Для абсолютно малых систем, таких как атомы, связанные в молекулу, это нарушало бы принцип неопределённости Гейзенберга.

Рис. 17.2. Вверху: шаростержневая модель молекулы углекислого газа CO ₂ . Внизу: три различные колебательные моды молекулы. Имеется две деформационные моды: одна из них изображена, а ещё одна такая же связана с движением атомов в направлении, перпендикулярном плоскости страницы

На рис. 17.2 изображена шаростержневая модель углекислого газа CO₂, а также показаны возможные её колебательные движения. Молекула CO₂ — линейная с двумя атомами кислорода, которые связаны двойными связями с центральным атомом углерода. Молекула CO₂ может совершать четыре различных колебательных движения, называемых колебательными модами. Связи могут растягиваться и сжиматься, а также деформироваться. Связи изображены пружинками. Чтобы понять природу этих колебательных мод, мы будем описывать соответствующие им движения так, как если бы они совершались классическими шариками на пружинах.

Колебательные моды углекислого газа

В симметричной моде центральный атом углерода не двигается. Как показано на схеме сплошными стрелками, два атома кислорода удаляются от углерода, растягивая пружины. Затем эти два атома возвращаются обратно к центральному атому углерода, сжимая пружины, что показано штриховыми стрелками. В классической системе из шаров на пружинах это движение повторяется, так что координаты атомов периодически меняются. Частота этих колебаний определяется массой грузов и упругостью пружин. В асимметричной моде два атома кислорода сначала сдвигаются вправо. Левый атом кислорода сжимает пружину, а правый растягивает её. Колебания не вызывают сдвига молекулы в целом. Поскольку оба атома кислорода движутся вправо, атом углерода смещается влево, сохраняя положение молекулы неизменным. Поскольку углерод движется влево, когда атомы кислорода смещаются вправо, в среднем положение всех атомов, называемое центром масс, не меняется. Эти движения обозначены сплошными стрелками. Затем направление движения каждого атома меняется на противоположное, как показано пунктирными стрелками.

Симметричные и асимметричные растяжения оставляют все три атома на одной прямой. В деформационной моде два атома кислорода сдвигаются вверх, а атомы углерода — вниз. При этом центр масс остаётся на месте. Затем атом углерода начинает двигаться вверх, а два атома кислорода — вниз. Кроме деформационной моды, изображённой на рис. 17.2, существует ещё одна. В нарисованной моде движения атомов происходят в плоскости страницы. Вторая деформационная мода точно такая же, за исключением того, что атомы движутся поперёк плоскости страницы.

Квантовые колебания обладают дискретными уровнями энергии

В классическом осцилляторе, сделанном из шаров, соединённых пружинами, энергия системы может меняться непрерывным образом. Рассмотрим симметричную моду. Три шара, связанные двумя идеальными пружинами, лежат на столе; трение и сопротивление воздуха отсутствуют. Если, взявшись за два внешних шара, в одинаковой мере растянуть две пружины иотпустить, то шары будут совершать симметричные упругие колебания. Поскольку пружины идеальные, трение о стол отсутствует и нет сопротивления воздуха (в реальной жизни такого, конечно, не бывает), колебания будут продолжаться вечно. Период и частота этих колебаний не зависят от того, насколько сильно были растянуты пружины. Период определяется упругостью пружин и массами шаров. Если растянуть пружины лишь чуть-чуть, то шары будут двигаться медленно. Их средняя кинетическая энергия будет мала. Если растянуть пружины сильно, шары станут двигаться быстро, а их средняя кинетическая энергия окажется велика. Энергия колебательной системы из шаров на пружинах меняется непрерывным образом. Она зависит только от того, насколько сильно мы растянем пружины.

Молекулы в действительности не являются шарами на пружинах. Это квантовомеханические системы, состоящие из атомов, соединённых химическими связями. Вместо непрерывного спектра энергий квантовые системы обладают дискретными колебательными энергетическими уровнями. Квантование их энергии происходит точно так же, как в задаче о частице в ящике, обсуждавшейся в главе 8. Герхард Херцберг (1904–1999) получил Нобелевскую премию по химии в 1971 году

«за вклад в понимание электронной структуры и строения молекул, особенно свободных радикалов».

Работа Херцберга по определению строения молекул основывалась во многом на его объяснении колебательных спектров молекул.

Энергия классического мяча для ракетбола меняется непрерывным образом, но энергия квантового мяча (частицы в ящике) привязана к энергетическим уровням (см. рис. 8.6). На рис. 17.3 изображена потенциальная кривая для вибрационной моды молекулы, подобная представленной на рис. 12.1, но теперь на ней также отмечены первые несколько колебательных энергетических уровней. И вновь, как и в случае частицы в ящике, низший энергетический уровень n=0 не соответствует нулевой энергии.

Энергия квантовых колебаний

Простейшая модель для колебательных уровней энергии даёт следующие их значения:

E=h∙ν∙(n+½),

где h — постоянная Планка, ν — частота колебаний, n — квантовое число, которое может принимать значения 0, 1, 2 и т. д. При n=0 энергия равна ½h∙ν. При n=1 энергия равна 3/2h∙ν. Таким образом, разность в энергии между низшим энергетическим уровнем и первым возбуждённым колебательным состоянием равна h∙ν. В этой модели все энергетические уровни отстоят друг от друга на одну и ту же величину h∙ν. В реальных молекулах c увеличением квантового числа энергетические уровни становятся ближе друг к другу. Для наших целей важна только разность между низшим энергетическим уровнем и первым возбуждённым.

Деформационная мода CO₂ поглощает на пике земного черноте́льного спектра

В нижней части рис. 17.3 изображены первые два колебательных энергетических уровня. Свет будет поглощаться при энергии, равной разности между этими уровнями, которая обозначена пунктирной стрелкой. Поскольку эта разность в энергии равна ∆E=h∙ν=c∙h/λ, измерение частоты (ν) и длины волны (λ) света, при которой он поглощается, даёт нам частоту осциллятора. Как показано на рисунке, для деформационных мод углекислого газа ∆E=667 см⁻¹. Деформационные моды имеют одинаковую частоту, поскольку различаются только направлением изгиба. (Энергию и частоту можно характеризовать числом колебаний волны на единицу длины (см⁻¹), если разделить энергию ∆E на c∙h.) Частота света, поглощаемого изгибами молекулы CO₂, почти в точности совпадает с пиком земного черноте́льного излучения. Растянуть химическую связь намного труднее, чем деформировать (то есть на это требуется больше энергии). Поэтому симметричная и асимметричная моды углекислого газа имеют намного более высокие частоты. Ни одна из них не даёт существенного вклада в поглощение земного черноте́льного излучения.

Рис. 17.3.Вверху: кривая потенциальной энергии, показывающая, как энергия зависит от длины химической связи, с отмеченными на ней колебательными квантовыми уровнями. Показаны только несколько первых энергетических уровней. Внизу: низший колебательный энергетический уровень n=0 и первый возбуждённый уровень n=1 для деформационной моды молекулы CO₂ (см. рис. 17.2). Данный переход (стрелка) будет поглощать и земное черноте́льное излучение (см. рис. 17.1)

Парниковый эффект CO₂ является кванотовомеханическим

Важнейший факт состоит в том, что на са́мом фундаментальном уровне вклад CO₂ в парниковый эффект и глобальное изменение климата является принципиально квантовомеханическим. Во-первых, связи, которые разрываются и создаются при горении природного газа, нефти и угля, определяются квантовой механикой, которая порождает молекулярные орбитали и определяет силу химических связей. От силы этих химических связей зависит количество энергии, высвобождаемой в расчёте на одну получающуюся молекулу CO₂, а на ещё более фундаментальном уровне форма спектра испускаемого Землёй черноте́льного излучения определяется квантовыми эффектами.

Черноте́льное излучение обсуждалось в главах 4 и 9. Объяснение Планком формы спектра чёрного тела и его изменения с температурой светящегося объекта было первым приложением квантовой теории. Полоса поглощения CO₂ располагается вокруг волны с частотой 667 см⁻¹ в результате квантования колебательных уровней молекул — чисто квантового эффекта. Деформационные моды молекулы CO₂ характеризуются квантовым переходом между колебательными состояниями n=0 и n=1, энергия которого соответствует ключевой частоте земного черноте́льного спектра. По мере того как мощные электростанции, многочисленные автомобили и самолёты, горящие тропические леса и т. п. выделяют углекислый газ, квантовое взаимодействие между CO₂ и земным инфракрасным черноте́льным излучением порождает парниковый эффект.

18. Ароматические молекулы

В главах 13 и 14 говорилось о двойных связях, а в главе 16 мы узнали о том, что двойные связи играют фундаментальную роль в определении биологических свойств жиров. Среди обсуждавшихся молекул были полиненасыщенные жиры, имеющие несколько двойных связей, однако эти двойные связи всегда разделяются некоторым числом одиночных связей. Например, на рис. 16.5 изображена шаростержневая модель молекулы ДГК — полиненасыщенной жирной кислоты с шестью двойными связями. Как легко заметить, между любыми двумя её двойными связями находятся две одиночные связи.

В этой главе мы познакомимся с разнообразными проявлениями множественных двойных связей, которые не разделяются несколькими одиночными связями. Квантовая теория показывает, что связи такого рода, обнаруживаемые в молекуле бензола и многочисленных других «ароматических» молекулах, могут объяснить электропроводность металлов, а также различия между металлами, полупроводниками и диэлектриками, которые будут обсуждаться в главе 19. Для понимания ароматических молекул и электропроводности металлов нам надо начать обсуждение с природы молекулярных орбиталей, которые возникают при взаимодействии одинаковых атомных орбиталей множества атомов.

Бензол: классический ароматический углеводород

На рис 18.1 изображена молекулярная диаграмма бензола, который состоит из шести атомов углерода и шести атомов водорода. Экспериментально было определено, что молекула бензола имеет правильную шестиугольную форму, а все её атомы (и углерод, и водород) лежат в одной плоскости. Угол между связями одного атома углерода с двумя ближайшими соседями составляет ровно 120°, и угол, образованный связью с водородом и с соседним углеродом, тоже равен 120°. Таким образом, три связи, образованные любым из атомов углерода, имеют треугольную геометрию, а значит, они образованы с помощью трёх sp²-гибридизированных атомных орбиталей каждого атома углерода. Итак, у всех атомов углерода остаётся по одной неиспользованной 2p-орбитали, расположенной перпендикулярно плоскости страницы. Обозначим её 2p_z. Мы знаем, что углерод всегда образует четыре связи. Здесь углерод связан лишь с тремя другими атомами с помощью трёх связей. 2p_z-орбитали должны служить для образования двойных π-связей, но где они располагаются в молекуле?

Рис. 18.1. Геометрия молекулы бензола C ₆ H ₆ . Бензол имеет форму правильного плоского шестиугольника

Где находятся двойные связи?

На рис. 18.2 изображены две возможные структуры с двойными связями. В обоих случаях каждый атом углерода образует четыре связи. Углерод образует три σ-связи — одну с водородом и по одной с двумя соседними атомами углерода. Каждый атом углерода участвует в двойной связи с одним из соседних атомов углерода. Диаграммы, изображённые справа и слева, идентичны, за исключением расположения двойных связей.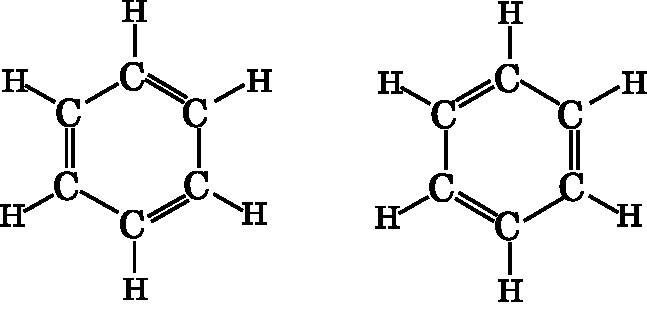

Рис. 18.2. Две возможные конфигурации двойных связей в бензоле. В обеих все атомы углерода образуют по четыре связи

Два момента, относящиеся к связям в молекуле бензола, отражены на рис. 18.2 неверно. При обсуждении двойных связей в главе 14 была приведена табл. 14.1, из которой видно, что двойные углерод-углеродные связи значительно короче одиночных. Двойная связь в этилене имеет длину 1,35 Å против 1,54 Å для одиночной связи в этане. Так что если в бензоле двойные и одиночные связи чередуются, то в нём должны чередоваться короткие и длинные углерод-углеродные звенья. Однако эксперименты убедительно показывают, что бензол является правильным шестиугольником и все углерод-углеродные связи в нём имеют одинаковую длину.

Если закрыть глаза на то, что диаграмма подразумевает неравную длину связей, то вторая проблема состоит в выяснении, какая из двух диаграмм верна — правая или левая? Нет никаких причин предпочесть одну другой. В первых попытках объяснения предполагалось, что связи постоянно переключаются между конфигурациями на правой и левой диаграммах. В результате такого перескакивания получается своего рода усреднённая структура. Эта идея является шагом в правильном направлении, но подлинный ответ, который впоследствии оказался применимым ко многим типам систем, касается природы образующихся молекулярных орбиталей.

Делокализация пи-связей

На рис. 18.3 схематически изображены атомные орбитали, участвующие в образовании молекулярных орбиталей бензола. Сверху нарисованы гибридные атомные орбитали, служащие для создания σ-связей. Каждый атом углерода использует три гибридные sp²-орбитали для образования трёх σ-связей — одной с атомом водорода и по одной для двух соседних атомов углерода. Образование этих трёх sp²-гибридизированных атомных орбиталей оставляет каждому атому углерода по одной избыточной p-орбитали. В верхней части рис. 18.3 за плоскость xy принята плоскость, содержащая атомы (плоскость страницы). Тогда у каждого атома углерода остаётся неиспользованная p_z-орбиталь, расположенная перпендикулярно плоскости страницы. Эти орбитали изображены в нижней части рисунка. Положительные и отрицательные лепестки орбиталей расположены над и под плоскостью кольца. На этой диаграмме длина связи между атомами углерода преувеличена, а ширина p_z-орбиталей приуменьшена, чтобы сделать изображение более понятным. В действительности же p_z-обитали перекрываются, что в более реалистичных пропорциях показано на рис. 14.15.

Эти шесть атомных p_z-орбиталей объединяются и образуют молекулярные орбитали. Без нарушения принципа Паули эти атомные орбитали могут содержать максимум 12 электронов. Поэтому шесть атомных орбиталей образуют суперпозицию и дают шесть молекулярных орбиталей (МО), которые также могут вмещать максимум 12 электронов. Эти МО не связаны с конкретным атомом или даже конкретной парой атомов. Они растянуты на всю систему из шести атомов углерода.

Рис. 18.3.Вверху: бензол и σ-связи. Каждый атом углерода образует три связи, используя три sp²-орбитали, лежащие в плоскости xy. У каждого атома углерода остаётся pz-орбиталь, перпендикулярная плоскости бензольного кольца. Внизу: p_z-орбитали углерода имеют положительные и отрицательные лепестки, которые расположены над и под плоскостью кольца. Длина связей здесь преувеличена, а ширина лепестков, наоборот, приуменьшена для того, чтобы иллюстрация стала понятнее. Лепестки соседних p_z-орбиталей перекрываются

Обсуждая молекулу водорода в связи с рис. 12.6, мы выяснили, что две атомные орбитали в ней объединяются и образуют две молекулярные орбитали — связывающую и разрыхляющую. В главе 13 мы разбирались с более крупными двухатомными молекулами, такими как F₂, O₂ и N₂. У этих элементов каждый атом имеет три p-орбитали, а шесть атомных орбиталей при объединении дают шесть π-МО — три связывающие и три разрыхляющие (см. рис. 13.5). Некоторые из этих двухатомных π-МО будут вырожденными, то есть обладающими одинаковой энергией.

Связывающие и разрыхляющие молекулярные орбитали

В бензоле шесть атомных p_z-орбиталей объединяются и образуют три связывающие МО и три разрыхляющие МО, как показано на рис. 18.4. Шесть 2p_z-орбиталей углерода, по одной у каждого атома, обладают одинаковой энергией. Это обозначено шестью близко расположенными линиями в левой части рис. 18.4. Они объединяются и образуют шесть МО с энергетическими уровнями, изображёнными в правой части рисунка. Энергия трёх из этих МО ниже, чем у атомных p_z-орбиталей, — это связывающие МО. Другие три МО обладают энергией более высокой, чем у атомных орбиталей, — это разрыхляющие МО.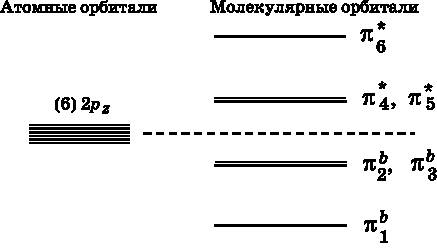

Рис. 18.4.Слева: бензол содержит шесть атомов углерода, каждый с 2p_z-орбиталью. Они обладают одинаковой энергией, что обозначено шестью близко расположенными линиями. Справа: шесть p_z-орбиталей объединяются и образуют шесть молекулярных π-орбиталей: три связывающие (b) и три разрыхляющие (*)

На рис. 18.5 изображены энергетические уровни связывающих и разрыхляющих орбиталей с размещёнными на них шестью электронами, по одному от каждого атома углерода. Мы помещаем электроны на низший доступный в соответствии с принципом Паули энергетический уровень. Принцип Паули (см. главу 11) утверждает, что на одной орбитали могут находиться не более двух электронов и что они должны иметь противоположные спины (один ориентирован вверх, другой — вниз). Первые два электрона занимают МО с наименьшей энергией. Следующие две МО имеют одинаковую энергию, что изображено двумя близко расположенными линиями. Каждую из этих МО занимают два электрона. Эти три МО, заполненные шестью электронами, являются π-связывающими. π-разрыхляющие МО остаются пустыми.

Рис. 18.5.Энергетические уровни молекулярных π-орбиталей бензола с размещёнными на них шестью электронами, занимающими низшие доступные энергетические уровни при соблюдении принципа Паули

Углерод-углеродная связь порядка 1,5

На рис. 18.5 видно, что шесть p_z-электронов углерода занимают три π-связывающие МО. Таким образом, имеются три π-связи, разделяемые шестью атомами углерода. Эти три π-связи добавляются к σ-связям, которые соединяют каждые два соседних атома углерода. Всего в результате у каждого атома углерода имеется 1,5 связи с соседними атомами: три π-связи разделяются шестью атомами углерода, внося в их соединения по половине связи. Такие связи между атомами углерода короче и сильнее одиночных углерод-углеродных связей, но они не настолько коротки и сильны, как настоящие двойные связи. π-связи фиксируют плоскую форму молекулы. Изгибы кольца, уводящие его от плоской формы, уменьшают перекрытие p_z-орбиталей и повышают энергию. На рис. 18.6 изображена молекулярная диаграмма бензола. Атомам углерода соответствуют вершины. Атомы водорода находятся на свободных концах отрезков, отходящих от углерода. Окружность обозначает систему делокализованных π-электронов.

Углеродные кольца с делокализованными π-связями входят во многие молекулы. Примером может служить нафталин, изображённый на рис. 18.7. Нафталин содержит десять атомов углерода, образующих два кольца по шесть атомов, к которым присоединены восемь атомов водорода. Две окружности изображают делокализованные молекулярные π-орбитали. Как и бензол, нафталин является плоским, а каждый атом углерода в нём имеет полторы связи с соседними атомами углерода.

Рис. 18.6.Молекулярная диаграмма бензола. В каждой вершине находится атом углерода, а атомы водорода располагаются на свободных концах отрезков, отходящих от углерода. В виде окружности изображены делокализованные молекулярные π-орбитали

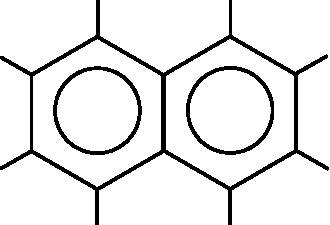Рис. 18.7.Молекулярная диаграмма нафталина. Нафталин содержит десять атомов углерода и восемь атомов водорода. Окружности изображают делокализованные молекулярные π-орбитали

Бензольные делокализованные молекулярные пи-орбитали

Бензол, нафталин и другие подобные молекулы называют ароматическими. Обычно они имеют приятный аромат. Нафталин используется против моли и имеет характерный запах. Духи содержат более сложные ароматические молекулы, в которые входит множество бензолоподобных колец, а также другие химические группы вместо атомов водорода. Небольшие изменения в молекулярной структуре приводят к изменению аромата, и именно поэтому разные духи пахнут по-разному.

В главе 8 мы обсуждали задачу о частице в ящике. На рис. 8.4 и 8.6 изображены волновые функции и энергетические уровни частицы в ящике. Волновая функция, связанная с низшим энергетическим уровнем, не имеет узлов. На следующем энергетическом уровне волновая функция имеет один узел, на следующем — два узла и т. д. Узел — это место, где волновая функция обращается в нуль, то есть вероятность обнаружить электрон равна нулю. Частица в ящике — это одномерная задача. Узел является точкой. В главе 10 мы анализировали волновые функции и энергетические уровни атома водорода. На рис. 10.2 и 10.6 изображены волновые функции атома водорода для состояний 1s, 2s и 3s. Эти волновые функции трёхмерные. Низшее энергетическое состояние (1s) не имеет узлов, следующее по энергии состояние (2s) имеет волновую функцию с одним узлом. Ещё более высокое энергетическое состояние (3s) имеет два узла. Эти узлы представляют собой трёхмерные поверхности, на которых вероятность обнаружения электрона равна нулю.

У бензольных π-МО число узлов также возрастает с увеличением энергии. На рис. 18.8 схематически изображены бензольные π-МО. Серым тоном показаны области высокой электронной плотности (высокой вероятности обнаружения электронов) для π-МО.

Эти трёхмерные электронные облака продолжаются над плоскостью страницы и за ней и не имеют чётких границ. Также показаны энергетические уровни шести p_z-электронов, которые заполняют связывающие МО с наименьшей энергией. МО с минимальной энергией не имеет узлов. Имеются два состояния со следующей по величине энергией. Обе такие МО имеют по одному узлу. Три МО без узлов и с одним узлом являются связывающими. Есть также два уровня со следующим по величине значением энергии. Эти МО имеют по два узла. МО с наивысшей энергией имеет три узла. Эти три МО, имеющие по два и три узла, являются разрыхляющими.

Рис. 18.8.Энергетические уровни бензольных молекулярных π-орбиталей и схематическое изображение формы соответствующих МО. С увеличением энергии число узлов тоже возрастает. МО с одинаковым числом узлов имеют одинаковую энергию

Сравнивая схемы МО с наименьшей и наибольшей энергией на рис. 18.8, нетрудно увидеть, почему первая МО является связывающей, а вторая — разрыхляющей. У МО с наименьшей энергией электронная плотность распределена между всеми атомами углерода. У разрыхляющей МО с наибольшей энергией между всеми атомами углерода находятся узлы, так что электроны на этой МО не будут связывать атомы углерода друг с другом. Две другие связывающие МО хотя и имеют более высокий энергетический уровень, чем связывающая МО с наименьшей энергией, в итоге всё же соединяют атомы углерода. Каждая из этих МО имеет по одному узлу. Та из них, что изображена слева, помещает электронную плотность между парами атомов углерода, находящимися слева и справа. МО, изображённая справа, помещает электронную плотность между тремя атомами углерода вверху и между тремя атомами углерода внизу. Несмотря на узлы, эти МО объединяются с МО, имеющей наименьшую энергию, и порождают три π-связи, которые разделяются между всеми шестью атомами углерода. Две вырожденные разрыхляющие МО имеют каждая по два узла. Та из них, что изображена слева, очевидно, не даёт вклада в связывание, поскольку не размещает электронную плотность между какими-либо двумя атомами углерода. МО, изображённая справа, хотя и помещает электронную плотность между двумя парами атомов углерода, но в совокупности с левой орбиталью не даёт связывания.

Поглощение света ароматическими соединениями

Для молекул ароматических соединений квантовая теория позволяет рассчитать молекулярные орбитали, а также их формы и размеры. Есть много способов проверить результаты квантовых вычислений путём сравнения с данными экспериментов. Один из наиболее полезных способов состоит в применении оптической спектроскопии для измерения длин волн (цветов) света, поглощаемого молекулами. Рассмотрим в качестве примера нафталин.

На рис. 18.7 представлена молекулярная диаграмма нафталина, содержащего десять атомов углерода. Каждый атом углерода вносит одну p_z-орбиталь с одним электроном в образование делокализованной системы π-электронов. Ещё три валентных электрона каждого атома углерода служат для образования σ-связей. Десять атомных p_z-орбиталей образуют π-систему, в которой, таким образом, будет десять молекулярных орбиталей: пять связывающих и пять разрыхляющих. В нафталине нет вырожденных МО, каждая имеет свою энергию. На рис. 18.9 схематически изображены энергетические уровни π-МО нафталина. Слева показаны энергетические π-уровни с десятью π-электронами, заполняющими пять связывающих МО. Разрыхляющие МО пустуют.

На рис. 18.9 показан эффект поглощения света. Поскольку энергетические уровни квантуются, молекула может поглощать свет лишь с определёнными значениями энергии. На рисунке ∆E — наименьшая энергия света, который может быть поглощён. Рассмотрим, что случится, если направить свет на образец с молекулами нафталина, начиная со света, который имеет слишком низкую энергию, чтобы быть поглощённым молекулами. Энергия света описывается формулой E=h∙ν, где h — постоянная Планка, а ν — частота. Итак, первоначально ∆E>h∙ν, то есть разница в энергии между верхней занятой молекулярной орбиталью (ВЗМО) и нижней свободной молекулярной орбиталью (НСМО) больше энергии фотонов, проникающих в образец. В результате они пройдут сквозь образец без поглощения. Теперь начнём изменять энергию света, повышая её (от красного к голубому). Когда h∙ν=∆E, свет поглощается, что проявляется в уменьшении количества излучения, проходящего сквозь образец. Электрон возбуждается, переходя с НСМО на ВЗМО. Это возбуждение показано в правой части рис. 18.9, где один электрон находится на ВЗМО и один электрон — на НСМО. В левой части рис. 18.9 на ВЗМО находятся два электрона, а на НСМО — ни одного.

Переход с ВЗМО на НСМО — это энергетически наименее затратный переход. Из рисунка видно, что связывающие МО находятся друг к другу ближе, чем ВЗМО и НСМО. Однако электрон не может возбудиться, перейдя с одной заполненной связывающей МО на другую. Если попытаться забрать электрон с одной связывающей МО и поместить его на другую, то получится МО с тремя электронами. Три электрона на МО нарушают принцип запрета Паули. Поэтому в нашем оптическом эксперименте, в котором цвет излучения меняется от красного к голубому (от низкой энергии к высокой), первым цветом (длиной волны), который подвергается поглощению, будет тот, что соответствует энергии ∆E. Значение ∆E можно вычислить на основе квантовой механики. Оно зависит от строения молекулы и взаимодействия атомных орбиталей, которые образуют молекулярные орбитали. Результаты квантовых вычислений в дальнейшем можно проверить, сравнивая с длинами волн, при которых будет происходить поглощение, по мере увеличения энергии света, смещающегося по спектру всё ближе к голубому. Второй раз поглощение произойдёт, когда свет сможет поднять электрон с ВЗМО на энергетический уровень, находящийся выше НСМО. Следующее поглощение соответствует переходу электрона с ВЗМО на орбиталь, которая на два энергетических уровня выше НСМО, и т. д.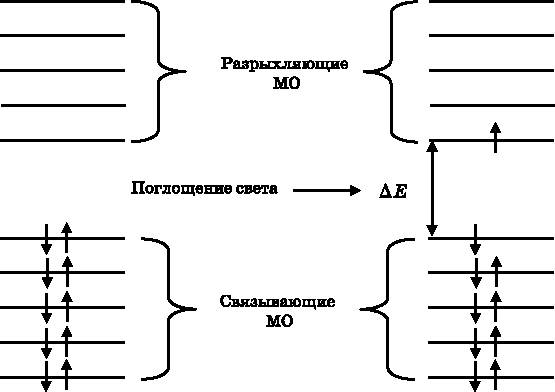

Рис. 18.9.Схема энергетических уровней молекулярных π-орбиталей нафталина. Имеются пять связывающих и пять разрыхляющих МО. Слева изображены десять π-электронов, заполняющих пять связывающих МО. Справа показан результат поглощения света: один из электронов увеличил свою энергию и поднялся на разрыхляющую МО

Нафталин с позиций задачи о частице в ящике

С помощью современной квантовой теории и компьютеров строение нафталина можно рассчитать с высокой точностью. Теория даёт значения длины связей и угла между ними. Например, длину связей можно вычислить с точностью до 0,001 нм, то есть до тысячной доли нанометра. На основе результатов этих вычислений можно также с высокой точностью рассчитать частоты, на которых поглощается свет. В вычислениях используются значения массы, числа электронов и заряда ядер. Расчёты охватывают как σ-, так и π-связи. Как уже говорилось, π-электроны не локализованы у одного или двух центров атомов углерода, а размазаны по всей углеродной структуре молекулы. Наименьшая энергия поглощения для нафталина, соответствующая переходу с ВЗМО на НСМО, характеризуется длиной волны 320 нм, которая лежит в ультрафиолетовой части оптического спектра.

Можно грубо рассчитать её, рассматривая π-электроны как частицы в ящике. В главе 8 задача о частице в ящике описывалась во всех подробностях. Если рассмотреть переход с ВЗМО на НСМО как переход электрона в ящике с уровня n=1 на уровень n=2 (см. рис. 8.7), то можно воспользоваться формулами, выведенными сразу после рис. 8.7. Для этого перехода получаем

∆E=3∙h²/8∙m∙L²,

где h — постоянная Планка, m — масса электрона, а L — длина ящика. Здесь мы примем значение L равным 0,51 нм, то есть поперечнику углеродной структуры нафталина. Тогда

∆E = 3∙(6,6∙10⁻³⁴)²/8∙(9,1∙10⁻³¹)∙(0,8∙10⁻⁹)² = 6,9∙10⁻¹⁹.

Преобразовав эту энергию в частоту путём деления на h, получаем: ν=1,04∙10¹⁵ Гц. Тогда длина волны поглощаемого света составит: λ=2,87∙10⁻⁷ м = 287 нм. Эта длина волны лежит дальше в ультрафиолетовой области, чем реальная, но всё же она не очень далека от наблюдаемого значения.

Расчёт для частицы в ящике показывает, что если частица с массой электрона заключена в ящике размером с молекулу нафталина, то первая линия поглощения будет находиться в ультрафиолетовом диапазоне. Удовлетворительная точность, полученная для нафталина при расчёте по модели частицы в ящике, представляет собой до некоторой степени случайную удачу. Даже если моделировать нафталин как частицу в ящике, это должен быть двух- или трёхмерный ящик, а не одномерный. Подобные расчёты обычно приводят к существенным ошибкам. Однако точные квантовомеханические вычисления позволяют определить строение молекулы и значительно более точные частоты поглощения света. Кроме того, если, например, заменить водород фтором, то квантовая теория точно предскажет, насколько изменятся частоты поглощения света фторнафталином по сравнению с обычным нафталином.

19. Металлы, изоляторы и полупроводники

На рис. 19.1 схематически изображена батарея, присоединённая к металлическому стержню. В качестве примера мы будем рассматривать натрий, но стержень может быть сделан из любого металла. Положительный полюс батареи вытягивает электроны из металлического стержня. Чтобы стержень не приобретал при этом положительный заряд, который станет притягивать электроны и остановит поток, он должен быть присоединён к отрицательному полюсу батареи.

Рис. 19.1. Металлический стержень, сделанный, например, из натрия, подключён проводами к батарее. Отрицательно заряженные электроны вытягиваются из металлического стержня положительным полюсом батареи. Электроны поступают в стержень из отрицательного полюса батареи

Электроны перетекают из отрицательного полюса батареи в положительный по стержню, сохраняя его нейтральность, то есть не позволяя ему приобретать электрический заряд. С тем же успехом вместо стержня электроны могут течь по спирали электрической лампочки фонарика. Проходящий по ней поток электронов заставляет спираль разогреваться до высокой температуры, испуская черноте́льное излучение в видимом диапазоне спектра.

Металлы

Делокализация молекулярных орбиталей в металлах

Каким образом электроны могут двигаться сквозь кусок металла? В чём разница между металлом и диэлектриком? Что такое полупроводники? Почему металлы нагреваются при движении электронов? Что такое сверхпроводимость?

Чтобы ответить на первые три вопроса, надо расширить обсуждение делокализованных молекулярных орбиталей, обнаруженных нами в молекулах ароматических соединений, таких как бензол и нафталин (см. главу 18), на МО макроскопических кусков металла и других материалов. Для ответа на два последних вопроса понадобится перейти от обсуждения влияния тепловых колебаний атомов, составляющих кусок металла, к обсуждению движения электронов в металле.

В главе 10 при обсуждении молекулы водорода мы узнали, что две атомные орбитали водорода объединяются и образуют две молекулярные орбитали — связывающую и разрыхляющую. В случае бензола мы увидели, что шесть атомных p_z-орбиталей — по одной от каждого атома углерода — образуют три связывающие и три разрыхляющие МО. У нафталина десять атомных p_z-орбиталей объединяются и образуют десять МО — пять связывающих и пять разрыхляющих. В каждом случае эти МО охватывают всю молекулу. В главе 11, посвящённой Периодической таблице элементов, мы говорили, что натрий (Na) является металлом, поскольку имеет один электрон (3s) сверх замкнутой неоновой конфигурации оболочки. Na легко отдаёт этот электрон для образования солей, таких как поваренная соль NaCl. В воде NaCl растворяется и превращается в ионы Na⁺ и Cl⁻. Как уже говорилось, в твёрдом состоянии Na является металлом и проводит электричество, и теперь мы готовы объяснить почему.

Рассмотрим для начала 3s-орбитали двух атомов натрия, которые находятся рядом друг с другом и взаимодействуют. У натрия 3s-электрон является валентным, то есть участвует в образовании связей. В верхней части рис. 19.2 показаны энергетические уровни двух атомных 3s-орбиталей, объединяющихся в молекулярные орбитали. Энергетический уровень одной из этих МО ниже, чем у атомных орбиталей. Это связывающая МО. Другая МО имеет более высокий уровень энергии — это разрыхляющая орбиталь. В средней части рисунка видно, что три атомные орбитали образуют три МО. Внизу представлена ситуация с шестью взаимодействующими атомами натрия. Шесть атомных 3s-орбиталей объединяются в шесть МО — три связывающие и три разрыхляющие.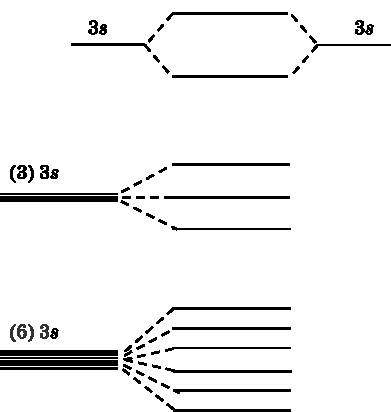

Рис. 19.2. Вверху: две атомные 3s-орбитали натрия взаимодействуют и порождают две молекулярные орбитали — одну с более низкой энергией (связывающую) и одну с более высокой (разрыхляющую). В середине: три атомные 3s-орбитали взаимодействуют и образуют три МО. Внизу: шесть атомных 3s-орбиталей объединяются в шесть МО

Каждый атом Na обладает одним 3s-электроном, который пойдёт на заполнение МО. В системе с шестью атомами натрия для заполнения МО будет шесть электронов. Каждая МО может принять два электрона с противоположными спинами (один направлен вверх, другой — вниз). Поэтому электронами будут заполнены три МО с наименьшими энергиями, то есть связывающие МО. Три МО с более высокими энергиями останутся пустыми.

Теперь нам надо рассмотреть, что произойдёт в случае очень большого числа взаимодействующих атомов натрия. Возьмём стержень длиной 10 см и диаметром 1 мм, состоящий из натрия (см. рис. 19.1). При таких размерах число атомов Na, которые будет содержать стержень, составит N=2∙10²¹ (два миллиарда триллионов) атомов Na. Два миллиарда триллионов атомных 3s-орбиталей объединяются в два миллиарда триллионов молекулярных орбиталей. Как и в случае МО бензола и нафталина, МО натриевого стержня следует считать распространяющимися на всю систему, то есть на весь кусок металла.

Кусок металла содержит огромное количество энергетических уровней МО, называемое зоной

На рис. 19.3 показаны энергетические уровни этой системы. Каждый из N атомов натрия обладает электроном на атомной 3s-орбитали. В отсутствие взаимодействия между атомами все эти атомные орбитали имеют одинаковую энергию. На рисунке это изображено группой близко расположенных линий с левой стороны. Чтобы показать наличие большого числа атомных уровней, линии нарисованы по отдельности, но все они обладают одинаковой энергией. Когда атомы взаимодействуют, N атомных орбиталей образуют N МО. Как мы уже видели ранее на примере молекул, МО имеют разные энергии. У некоторых из этих МО энергия ниже, чем у атомных орбиталей, у других — выше. Это изображено в правой части рисунка более широким набором по-прежнему тесно расположенных линий. Система энергетических уровней МО на рис. 19.3 такая же, как на рис. 18.8, 18.9 и 19.2, с той лишь разницей, что имеется намного больше энергетических уровней, интервалы между которыми намного меньше. В этом случае говорят о зоне состояний.

Квантовая теория говорит, что ширина зоны состояний, то есть разность энергии между МО с наибольшей и наименьшей энергией, всего в несколько раз больше, чем разность в энергии двух МО, возникающих при взаимодействии двух атомов натрия (см. рис. 19.2, вверху). Таким образом, в нашем примере с двумя миллиардами триллионов атомов Na в относительно узком диапазоне энергий имеется два миллиарда триллионов энергетических уровней. В результате эти уровни оказываются расположенными так близко, что энергия внутри зоны меняется фактически непрерывно.

Рис. 19.3. В куске металлического натрия имеется N атомов. У каждого атома есть электрон на 3s-орбитали. Все вместе они представлены тесно расположенными линиями в левой части рисунка. Все они обладают одинаковой энергией. N атомных 3s-орбиталей взаимодействуют, образуя N молекулярных орбиталей, энергетические уровни которых показаны справа. Энергетические уровни МО настолько близки друг к другу, что их энергии образуют практически непрерывную зону состояний. Уровень Ферми соответствует самой высокой заполненной орбитали

Расселение электронов

Итак, есть N атомов натрия, каждый с одним 3s-электроном. Нам требуется поместить эти N электронов на соответствующие МО, как мы это делали с небольшими молекулами в главах 12 и 13 и как показано на рис. 18.8 и 18.9. Делокализованные МО металлического натрия подобны любым другим орбиталям, а значит, они подчиняются трём правилам расселения электронов, которые обсуждались в главе 11: сначала заселяются уровни с наименьшей энергией; на одной орбитали может находиться не более двух электронов, причём они должны иметь спаренные спины (принцип запрета Паули); по возможности спины не спариваются (правило Хунда).

На рис. 19.3 показано расселение электронов. Первый электрон занимает самый нижний энергетический уровень. Следующий электрон заселяется на тот же уровень с противоположным спином, то есть на нём будет одна стрелка вверх и одна стрелка вниз. Три электрона не могут располагаться на низшем энергетическом уровне, поскольку это нарушило бы принцип Паули. Поэтому третий электрон заселяется на уровень, который на один выше самого нижнего. Четвёртый электрон размещается на том же уровне со спаренным спином. Так продолжается до тех пор, пока по молекулярным орбиталям не будут размещены все N электронов.

Уровень Ферми

Имеется N энергетических уровней МО и N электронов. Однако на каждом уровне может находиться два электрона, поэтому заполнена будет только нижняя половина зоны энергетических уровней. Это похоже на бензол (см. рис. 18.8) и нафталин (см. рис. 18.9), у которых тоже заполнена только нижняя половина МО. Энергия самой высокой из заполненных орбиталей называется уровнем Ферми — в честь Энрико Ферми (1901–1954). Ферми как физик работал во многих областях науки, включая теорию твёрдого тела, в частности металлов, и теорию ядерных реакций. Он внёс значительный вклад в развитие ядерной энергетики. В 1938 году он получил Нобелевскую премию по физике

«за доказательство существования новых радиоактивных элементов, полученных при облучении нейтронами, и связанное с этим открытие ядерных реакций, вызываемых медленными нейтронами».

Как мы увидим, уровень Ферми чрезвычайно важен.

Уровень Ферми — это наивысшая заполненная МО при абсолютном нуле температуры, то есть при температуре 0 K, где K означает кельвины. 1 K равен 1 °C, однако нуль шкалы Кельвина соответствует абсолютному нулю температур, то есть 0 K — это −273 °C. Мы кратко обсуждали, как тепло в системах молекул, таких как вода, вызывает дрожание молекул. В главе 15 отмечалось, что тепловые движения молекул воды ответственны за разрушение водородных связей между ними. По мере понижения температуры тепла (тепловой энергии) становится всё меньше, и движение атомов и молекул замедляется. Абсолютный нуль (0 K) — это температура, при которой вообще нет тепла, заставляющего атомы и молекулы двигаться. Уровень Ферми определяется именно как энергия наивысшей заполненной МО при 0 K.

Как электроны движутся сквозь металл

Как показано на рис. 19.1, электроны входят в металлический стержень с одной стороны и покидают его с другой. Это возможно, поскольку электроны находятся на делокализованных МО, растянутых на весь кусок металла. Однако квантовая теория показывает, что если все электроны занимают только МО ниже уровня Ферми, то они не будут двигаться в каком-либо определённом направлении. В реальности металлы трёхмерны, но в данном обсуждении мы будем рассматривать только одно измерение за раз. В нашем металлическом стержне даже тогда, когда он не присоединён к батарее, электроны, находящиеся на МО, тем не менее постоянно движутся. Хотя электроны описываются в терминах квантовомеханических волновых функций, они обладают кинетической энергией. Поэтому можно подсчитать скорость электрона. Электроны на некоторых МО можно рассматривать как движущиеся вправо. Имеются соответствующие им МО с точно такой же энергией, но с электронами, движущимися влево. Когда все МО заполнены, как показано на рис. 19.3, электрического тока не будет, поскольку одинаковое число электронов движется влево и вправо. В трёхмерном случае для любого выбранного направления у электрона будет равная вероятность двигаться в этом направлении или в диаметрально противоположном.

Однако когда металлический стержень на рис. 19.1 присоединяется к батарее, всё меняется. Один конец стержня соединён с положительным полюсом батареи, а другой — с отрицательным. Подключение к батарее меняет условия существования электронов. Без батареи электроны ощущают положительные заряды атомов натрия и отрицательные заряды других электронов. Любой отдельный электрон в середине стержня не чувствует разницы между правым и левым. Однако при подключении к батарее появляется дополнительный действующий фактор — созданное ею внутри металла электрическое поле. Электроны притягиваются к положительному концу и отталкиваются от отрицательного конца. В результате система меняется, поскольку некоторые электроны оказываются на уровнях выше уровня Ферми, который был без батареи (см. рис. 19.4). Состояние электронов в системе меняется так, что становится больше электронов, движущихся к положительному концу металлического стержня, чем движущихся к отрицательному.

Рис. 19.4. Схематическое изображение уровней 3s-зоны натрия, представленных на рис. 19.3, с поправкой на воздействие подключения к батарее. В результате некоторые электроны оказываются выше уровня Ферми без батареи, переходя с заполненных МО на пустые. Эти электроны изображены здесь стрелками выше уровня Ферми

Согласно квантовой теории, для наличия электронной проводимости требуется наличие электронов, находящихся выше уровня Ферми. Поскольку энергетический зазор между уровнями исчезающе мал, даже очень низкого напряжения, приложенного к стержню и порождающего ничтожное электрическое поле, достаточно, чтобы некоторые электроны оказались выше уровня Ферми. Результатом становится появление электрического тока в металлическом стержне. Электроны покидают положительный конец стержня и заменяются электронами, входящими со стороны отрицательного конца. При более сильном электрическом поле (более высоком напряжении) над уровнем Ферми, соответствующем нулевому полю, оказывается больше электронов, и электрический ток становится сильнее. Детальная квантовая теория электропроводности металлов говорит, что ток будет возникать под действием приложенного электрического поля даже при нулевой абсолютной температуре. Для того чтобы проводить электричество, металлам не требуется тепло. Ниже мы увидим, что в случае полупроводников это не так, а также что тепло, имеющееся при температуре выше 0 K, на самом деле мешает электрической проводимости в металлах.

Диэлектрики

Диэлектрики не проводят ток вследствие заполненности зоны

Металлы хорошо проводят электричество даже при 0 K, поскольку электроны заполняют только часть зоны состояний (см. рис. 19.3 и 19.4). Даже очень слабое электрическое поле (напряжение) будет поднимать электроны над уровнем Ферми. Диэлектрики — это материалы вроде стекла или пластика, которые не проводят электричество ни при какой температуре. Зонная структура диэлектрика схематически изображена на рис. 19.5.

В металлическом натрии 3s-электроны являются валентными. Валентная зона заполнена лишь наполовину. В таком диэлектрике, как кварц (SiO₂, диоксид кремния), который очень похож на стекло, совместно используемые электроны доводят электронные оболочки до замкнутости. Взаимодействие атомов в кристалле кварца порождает зону состояний с делокализоваными МО, как и в металле. Однако валентная полоса целиком занята. На каждый МО находится по два электрона, поскольку имеется N МО, но 2N электронов. Таким образом, все МО — от самого низкого до самого высокого энергетического уровня в пределах зоны — содержат по два электрона. Заполненность зоны представлена на рис. 19.5 присутствием стрелок как на нижних, так и на верхних уровнях зоны. Эта заполненная зона должна сопоставляться с наполовину заполненной зоной металлического Na, изображённой на рис. 19.3.

Рис. 19.5. Схематическое изображение зонной структуры диэлектрика. Имеется заполненная зона с двумя электронами на каждой МО. Есть свободная зона с гораздо большими значениями энергии

В диэлектриках широкая запрещённая зона

Существуют свободные атомные орбитали со значительно более высокой энергией, и они тоже образуют МО. Однако нет электронов, которые могли бы занять эти МО. Поэтому следующая по высоте энергетическая зона совершенно пуста. Разность энергии между верхним краем заполненной зоны и нижним краем незаполненной зоны называется запрещённой зоной. Уровень Ферми находится у верхнего края заполненной зоны.

Выше уже обсуждалось на качественном уровне (а в квантовой теории это аккуратно обосновывается), что для электропроводности требуется наличие электронов на МО с энергией выше уровня Ферми. Когда в веществе создаётся электрическое поле (путём подключения к батарее или другому источнику напряжения), природа делокализованных состояний меняется. В металлах, поскольку зона лишь наполовину заполнена, а энергетические уровни разделены ничтожными интервалами, приложенное напряжение приводит к тому, что некоторые электроны оказываются выше уровня Ферми, соответствующего нулевому полю, и электроны начинают течь по металлу. В изоляторе следующий уровень над уровнем Ферми находится в пустой зоне. Запрещённая зона велика, и приложение электрического поля не может изменить систему в достаточной степени, чтобы в пустой зоне появились электроны. Поэтому приложить электрическое поле к изолятору, в отличие от металла, недостаточно для того, чтобы возникла проводимость.

Другая возможность состоит в том, что тепловая энергия возбуждает электроны заполненной зоны, забрасывая их в пустую зону. Изоляторы обладают тем свойством, что энергетическая ширина запрещённой зоны намного больше тепловой энергии. С повышением температуры количество тепловой энергии возрастает. Однако в изоляторах запрещённая зона настолько велика, что материал будет разрушен при температуре, которая всё ещё недостаточно высока, чтобы термически возбудить электроны, подняв их из заполненной зоны в пустую. Таким образом, невозможно ни изменение состояния электронов за счёт приложенного электрического поля, ни тепловое возбуждение электронов, и поэтому диэлектрики не проводят электричество.

Полупроводники

В полупроводниках запрещённая зона небольшая

Полупроводники похожи на диэлектрики, но в отличие от них имеют небольшую запрещённую зону. Зонная структура полупроводника схематически изображена на рис. 19.6. В полупроводнике, таком как кремний (Si), имеется достаточное число электронов, чтобы целиком заполнить валентную зону. При 0 K, когда нет тепловой энергии для возбуждения электронов, все они спарены и находятся в валентной зоне. Уровень Ферми соответствует верхнему краю заполненной валентной зоны. Таким образом, при 0 K кремний является диэлектриком. Однако в кремнии и других полупроводниках ширина запрещённой зоны невелика. При комнатной температуре тепловой энергии уже достаточно, чтобы возбудить некоторые электроны и поднять их в следующую зону над уровнем Ферми. Тепловая энергия заключена в движении атомов полупроводника.

На рис. 19.6 проиллюстрировано возбуждение электронов с переходом в следующую зону, находящуюся выше уровня Ферми. Электроны, которые возбуждаются, переходя с заполненных МО валентной зоны на свободные МО зоны проводимости, изображены на этом рисунке стрелками, находящимися выше уровня Ферми. Благодаря электронам, находящимся выше уровня Ферми, полупроводники, такие как кремний, могут проводить электричество. Электроны, находящиеся в зоне проводимости, называются электронами проводимости.

Полупроводники проводят электричество не так хорошо, как металлы, поскольку в них намного меньше электронов проводимости. В металлах нет запрещённой зоны. Большое число электронов легко поднимается над уровнем Ферми. В полупроводниках запрещённая зона есть, но она достаточно мала, чтобы тепловая энергия могла возбудить некоторые электроны и поднять их в зону проводимости, лежащую выше уровня Ферми. При понижении температуры в полупроводниках становится всё меньше и меньше электронов проводимости, способных переносить электрический ток.

При очень низкой температуре полупроводники становятся диэлектриками. Единственное различие между полупроводниками и диэлектриками заключается в ширине запрещённой зоны. Чипы в вашем компьютере, которые состоят в основном из кремниевых полупроводников, перестанут работать, если их сильно охладить. Компьютеры и электроника на спутниках должны пребывать в тепле, иначе они выйдут из строя.

Рис. 19.6. Схематическое изображение зонной структуры полупроводников. Валентная зона практически целиком заполнена. Энергетический интервал, отделяющий следующую зону, относительно мал. Некоторые электроны термически возбуждаются и поднимаются выше уровня Ферми в зону проводимости

Тепловая энергия влияет на электропроводность металлов

Тепловая энергия требуется полупроводникам для появления электронов проводимости. Она также сильно влияет на электропроводность металлов, хотя для появления в них электронов проводимости тепловая энергия им не нужна. В куске металлического провода, подсоединённого к батарее, электроны движутся в направлении положительного полюса. По мере того как электроны покидают провод, они восполняются электронами, поступающими из отрицательного полюса батареи. Ток (электронов), проходящий по куску провода, вызывает повышение температуры. Нагревательные элементы в электрических печах и обогревателях становятся очень горячими из-за протекающего по ним сильного тока. Они разогреваются настолько, что начинают светиться красным, — это черноте́льное излучение металла.

Как уже говорилось, электроны легко проходят сквозь кусок металла, поскольку они находятся на делокализованных МО, охватывающих металл целиком. Требуется лишь электрическое поле (подключение к батарее или другому источнику напряжения), чтобы заставить их двигаться в определённом направлении. Вопрос же состоит в том, почему поток электронов вызывает нагревание металла.

Электроны в металле следует представлять себе волновыми пакетами, которые более или менее локализованы. Мы обсуждали волновые пакеты в главе 6 в связи с принципом неопределённости Гейзенберга. Электронные волновые пакеты в металле образуются из суперпозиций делокализованных волновых функций электронных МО аналогично фотонным и электронным волновым пакетам в вакууме, которые являются суперпозициями делокализованных импульсных состояний. Электроны заряжены отрицательно, поэтому электронный волновой пакет несёт отрицательный заряд. Электрон ускоряется в направлении положительного полюса. Это ускорение приводит к увеличению кинетической энергии электрона.

Фононы — вибрации твёрдого тела

В главе 17 в связи с парниковыми свойствами углекислого газа мы коротко обсудили квантование колебаний молекул. Кусок металла, состоящий из атомов, тоже испытывает квантованные колебания. Атомы в кристаллической решётке металла могут подрагивать на своих местах. Несмотря на это дрожание, они остаются в среднем на одном месте. Движение каждого атома связано с движениями других атомов таким же образом, как движение каждого атома в молекуле CO₂ связано с движениями остальных (см. рис. 17.2). Молекула CO₂ может испытывать несколько различных типов колебаний: в симметричной, асимметричной и двух деформационных модах. Эти три разных типа мод обладают колебательными энергиями (частотами), которые очень сильно отличаются друг от друга.

В кристаллической решётке металла каждый атом может двигаться во всех трёх измерениях. Для N атомов существует 3N колебаний решётки, где вновь N — число атомов в куске металла. Для любого конечного куска металла имеется огромное число колебаний, складывающееся в колебательную полосу вместо нескольких дискретных частот. При низкой температуре тепловые колебания охватывают только нижнюю часть значений энергии этой полосы. При высокой температуре возбуждается больше колебаний решётки с более высокими значениями энергии колебаний. Возбуждённые колебания обладают кинетической энергией. Именно эта энергия возбуждённых колебаний воспринимается нами как тепло.

Квантованные колебания решётки называются фононами. Такое название связано с тем, что фононы в некоторых фундаментальных аспектах квантовой теории напоминают фотоны. Каждый фонон является делокализованной волной колебаний, которая распространяется на всю кристаллическую решётку. Волны решётки могут образовывать более или менее локализованные волновые пакеты за счёт суперпозиции большого набора длин волн. Более или менее локализованный фононный волновой пакет совершенно аналогичен фотонному или электронному волновому пакету, которые упоминались чуть выше, а подробно обсуждались в главе 6. Фононы — это движущиеся волновые пакеты механической и тепловой энергии. Фононный волновой пакет можно рассматривать как движущуюся область более или менее локализованного дрожания атомов.

Электронные и фононные волновые пакеты взаимно рассеиваются

Электронный волновой пакет, который ускоряется в положительном направлении, может провзаимодействовать с фононом. Фонон заставляет двигаться положительно заряженные атомные ядра. Отрицательно заряженные электроны испытывают влияние со стороны этих движущихся положительных зарядов. Взаимодействие электронов и протонов называется рассеянием и схематически изображено на рис. 19.7.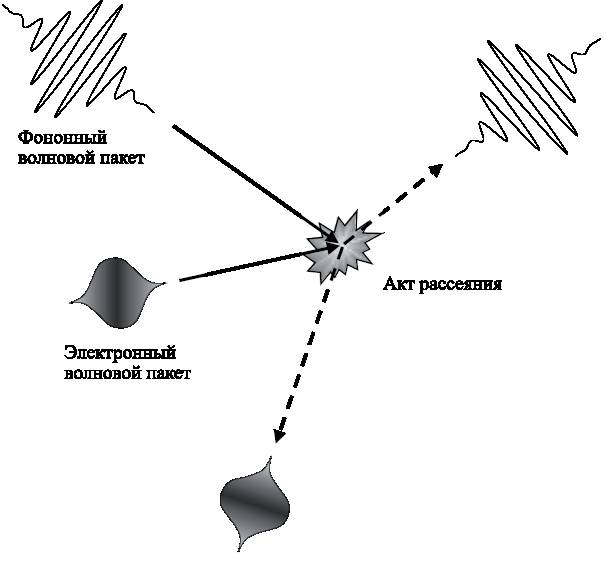

Рис. 19.7. Схема электрон-фононного рассеяния. Взаимодействие электрона и фонона вызывает изменение направления движения волновых пакетов

Электронные и фононные волновые пакеты распространяются в определённых направлениях. Электрон, ускоряемый электрическим полем, «сталкивается» с фононом. Происходит рассеяние, после которого в общем случае оба волновых пакета начинают двигаться по новым направлениям. Электрон вновь будет ускоряться электрическим полем в положительном направлении. Через некоторое время он опять встретится с фононом и рассеется. При каждом рассеянии электрон отдаёт фонону часть своей кинетической энергии, полученной при ускорении электрическим полем (за счёт источника напряжения).

Акты рассеяния приводят к двум эффектам. Во-первых, они мешают электронам двигаться прямо к положительному полюсу батареи. Во-вторых, приводят к увеличению кинетической энергии фононов. Электроны теряют энергию, а фононы её приобретают. Электрон-фононное рассеяние приводит к уменьшению электропроводности металлов, поскольку электроны постоянно попадают в столкновения, сбивающие их с направления на положительный конец провода, к которому они стремятся. Это называется электрическим сопротивлением. При очень низкой температуре фононов мало, так что электроны могут пройти большой путь между двумя актами рассеяния. В результате им легче достичь положительного конца. С повышением температуры становится всё больше и больше фононов, поскольку фононы — это тепло. При высокой температуре электроны проходят меньший путь, прежде чем их направление изменится, и это мешает им двигаться к положительному электроду. В результате при повышении температуры электропроводность уменьшается (сопротивление возрастает).

Электрон-фононное рассеяние приводит к нагреванию металла

Поскольку акты рассеяния приводят к увеличению кинетической энергии фононов, они повышают температуру металла. Температура — это мера тепла, содержащегося в веществе. Тепло — это кинетическая энергия движения атомов. Если множество электронов движется сквозь металл, испытывая рассеяние, то провод получает много дополнительного тепла и его температура повышается. Однако с повышением температуры фононов и актов рассеяния становится ещё больше, и температура продолжает повышаться.

Этот процесс можно наблюдать при включении электрической печи: на то, чтобы её элемент разогрелся до красного свечения, требуется некоторое время. Когда вы включаете печь, её нагревательный элемент находится при комнатной температуре. С появлением электрического тока начинают происходить электрон-фононные рассеяния, повышающие температуру. Это означает, что появится ещё больше фононов и будет ещё больше актов рассеяния, а в проводе выделится ещё больше тепла. Провод достигнет постоянной высокой температуры, определяемой силой тока (выбранной регулятором печи) в начальный момент при комнатной температуре, когда печь только включили.

В нормальном металле электроны подвергаются электрон-фононному рассеянию при любой температуре. Поэтому кусок провода имеет электрическое сопротивление при любой температуре, отличной от абсолютного нуля (0 K). При абсолютном нуле тепла нет, а значит, нет и фононов. Однако достичь абсолютного нуля невозможно. Используя крайне специфические экспериментальные методы, можно достичь очень низких температур, например одной миллионной доли градуса над абсолютным нулём, но даже при этой невероятно низкой температуре существует некоторое количество фононов и происходят акты электрон-фононного рассеяния. Кроме того, если начать пропускать сколько-нибудь значительный ток по куску обычного провода, охлаждённого до очень низкой температуры, он нагреется. Как упоминалось в главе 17, линии электропередачи, идущие от электростанций к городам, теряют много электроэнергии. Теперь мы понимаем почему. Это связано с электрическим сопротивлением проводов, то есть с электрон-фононным рассеянием.

Сверхпроводимость

Вещества, которые не имеют электрического сопротивления при отличной от абсолютного нуля температуре, называются сверхпроводниками, а течение электронов по сверхпроводящему куску провода называется сверхпроводимостью. В металлах сверхпроводимость возникает только при очень низких температурах. Голландский физик Хейке Камерлинг-Оннес (1853–1926) открыл сверхпроводимость в 1911 году, когда охладил ртуть до 4 K (−269 °C). Он обнаружил, что её сопротивление упало до нуля. Приведём также примеры некоторых других металлов и максимальные значения температуры, при которых они являются сверхпроводящими: ниобий — 9,26 K, свинец — 7,19 K, ванадий — 5,3 K, алюминий — 1,2 K и цинк — 0,88 K.

Явление сверхпроводимости смогли объяснить лишь десятки лет спустя. В 1972 году три американских физика — Джон Бардин (1908–1999), Леон Купер (р. 1930) и Джон Шриффер (р. 1931) — получили Нобелевскую премию по физике

«за создание теории сверхпроводимости, обычно называемой БКШ-теорией».

БКШ-теория была разработана в 1957 году и является исчерпывающим квантовомеханическим объяснением электрон-фононного взаимодействия при низкой температуре. В 1956 году Леон Купер показал, что электрон-фононные взаимодействия могут приводить к спариванию электронов. Два электрона в некотором смысле объединяются, хотя физически они находятся далеко друг от друга. В БКШ-теории была использована эта идея и показано, что такие куперовские пары не испытывают обсуждавшегося выше электрон-фононного рассеяния, которое служит причиной электрического сопротивления. Когда нет электрон-фононного рассеяния, электроны движутся сквозь металл, не испытывая сопротивления, даже при температуре, отличной от абсолютного нуля. Поскольку сопротивление отсутствует, то нет и потерь электроэнергии, несмотря на прохождение сильного тока.

Сверхпроводники уже сегодня имеют множество применений, и не вызывает сомнения появление в будущем ещё более важных и широко распространённых приложений. Для магнитно-резонансной томографии (МРТ) требуются очень мощные магниты. Большой цилиндр МРТ, внутрь которого помещают пациента, — это сверхпроводящий электромагнит. Магнитное поле появляется, когда электрический ток течёт по свёрнутому в катушку проводу. Чтобы получить сильное магнитное поле, необходим очень сильный ток и большое количество провода, свёрнутого в катушку. До появления сверхпроводящих электромагнитов не удавалось получить достаточно сильных магнитных полей. Провод слишком сильно нагревался, и его охлаждение становилось огромной проблемой. Теперь провод делают из сверхпроводящего металла, такого как ниобий. Когда в катушке запускается течение электронов, два её конца соединяют. Электроны продолжают кружиться по катушке. Поскольку сопротивления нет, то нет и потерь энергии, а значит, не требуется подводить к катушке дополнительное электричество. Без сверхпроводимости у нас не было бы МРТ.

Ещё одна большая надежда — это сверхпроводящие линии электропередачи. Такие линии электропередачи полностью исключили бы потери электроэнергии. Появилась бы возможность передавать электричество на гораздо большее расстояние, чем сегодня. Проблема состоит в том, что металлические сверхпроводники должны быть настолько холодными, что использовать их для линий электропередачи непрактично. Существуют новые типы высокотемпературных сверхпроводящих материалов. Их открыли в 1986 году Карл Мюллер (р. 1927) и Йоханнес Беднорц (р. 1950). Они получили Нобелевскую премию по физике в 1987 году

«за важный прорыв в физике, выразившийся в открытии сверхпроводимости в керамических материалах».

На сегодня сверхпроводимость в таких керамических материалах не получила исчерпывающего теоретического объяснения. Сверхпроводимость в них может наблюдаться при температурах до 138 К. Эта температура достаточно высока для многих практических приложений. Поскольку высокотемпературные сверхпроводники являются керамическими, из них нельзя делать провода, как из металлов^{38}. Однако в будущем исследования могут привести к появлению более удобных для использования высокотемпературных сверхпроводников, которые революционизируют передачу электроэнергии и другие области электроники.

20. Квантовое мышление

Когда отец, держа младенца на руках, показывает на небо и говорит: «Это Луна», младенец, конечно, замечает в небе яркий объект. Он может запомнить, что этот свет в небе называется «Луна», но он не понимает, что такое Луна и где она находится. В возрасте 7–8 лет представление о том, что такое Луна, становится более глубоким. Ребёнок уже знает, что Луна очень сильно отличается от уличного фонаря на углу квартала, что она находится очень далеко и что дотронуться до неё и забраться на неё нельзя, хотя много лет назад люди всё-таки там побывали. Взрослея, человек приобретает адекватное представление о Луне, даже если не научится рассчитывать её орбиту вокруг Земли с помощью ньютоновской классической механики. Взрослый знает, что видимое движение Луны по небу связано с вращением Земли, что Луна находится очень далеко, но гораздо ближе, чем планеты Солнечной системы, и что человек, находящийся на Луне, весит гораздо меньше и прыгнуть может гораздо выше, чем на Земле, поскольку масса Луны меньше и потому сила тяжести там слабее.

Опыт учит нас понимать классический мир

Наше понимание Луны углубляется с возрастом не только благодаря образованию, но и за счёт интуитивной логики в описании Луны как объекта, обращающегося вокруг Земли. Это описание во многих отношениях совместимо с нашим повседневным опытом. Если бросить бейсбольный мяч, он опишет дугу, прежде чем упадёт на землю. Если бросить его сильнее и направить выше, он поднимется на бóльшую высоту и улетит дальше, описав до падения дугу большего размера. Легко и естественно расширить это представление и понять, что ракета, разогнав объект до очень высокой скорости и направив его очень высоко, заставит его описать дугу, которая охватит половину Земли, что, по сути, и делается межконтинентальными ракетами. После этого уже нетрудно согласиться, что если с помощью ещё более мощной ракеты разогнать объект ещё сильнее, то описываемая им дуга превратится в орбиту вокруг Земли. Тогда становится ясно, что Луна — это просто очень большой объект, движущийся достаточно быстро, чтобы обращаться по орбите вокруг Земли.

Наша способность перейти от бейсбольного мяча к обращению Луны вокруг Земли основывается на повседневном опыте применения классической механики. Однако для того, чтобы собрать все факты воедино, требуется способность к абстрактным рассуждениям. В древности люди разумно полагали, что Луна обращается вокруг Земли. В конце концов, невооружённым глазом видно, что она движется по небу. Можно проделать простой эксперимент, чтобы понять, почему Луна выглядит обращающейся вокруг Земли. Встаньте посреди комнаты, в которой на стене висит лампа, и начните медленно поворачивается кругом. Вы увидите, что светильник приходит в движение. Повернувшись к нему спиной, вы перестанете его видеть. По мере вращения светильник появится на краю вашего поля зрения, переместится в его центр, а потом исчезнет за другим краем. Он не появится вновь, пока вы не совершите ещё полоборота. Объединяя этот простой опыт с тем, что мы знаем о бейсбольных мячах и межконтинентальных ракетах, нетрудно принять, а на самом деле и понять, что Луна обращается вокруг Земли и что Земля вращается вокруг своей оси, вызывая «восходы» и «заходы» Луны.

Наш опыт и фундаментальная природа систем, подчиняющихся законам классической механики, позволили нам выработать интуицию, описывающую поведение многих повседневно окружающих нас вещей. Даже новичок при игре в бильярд быстро схватывает, что если направить биток так, чтобы он ударил по левой части другого шара, тот отскочит вправо. Столкновение бильярдных шаров — это классический процесс, и шары движутся в соответствии с законами классической механики по чётко определённым траекториям. Однако мир вокруг нас, управляемый законами квантовой механики, по большей части лежит за рамками наших представлений и понимания. Когда дело доходит до явлений, которые определяются свойствами абсолютно малых систем, большинство людей подобны младенцу, глядящему на Луну: они видят явление, но не понимают того, что видят.

Понимание того, что мы видим вокруг себя, требует некоторого знания квантовой механики

Почему это должно нас беспокоить? Можно прожить всю жизнь, видя Луну и не имея никакого представления о том, чем она в действительности является. Человек может просыпаться утром, идти на работу, есть, спать, иметь семью, не зная, что представляет собой Луна, и быть при этом совершенно счастливым. Можно также не иметь никакого понятия о том, благодаря чему вещи вокруг нас обретают свои свойства. Мы живём в море физических явлений, которое качает нас на своих волнах. Мы можем оказаться не способны управлять физическим миром вокруг нас, но разумно ли полностью отказываться понять его? Хотим ли мы уподобляться младенцу или, ещё хуже, взрослому, не имеющему представления о Луне? Действительно ли мы не хотим иметь никакого понятия о том, почему нагревательный элемент в электрической печи становится горячим? Я считаю, что мир становится интереснее, когда мы проявляем некоторое уважение к природе окружающих нас вещей. Физический мир — от биологических молекул до электрической проводимости — управляется квантовыми явлениями. И раз уж мы плывём по океану квантовой физики, некоторое знание квантовой теории только повышает нашу оценку чудес природы.

Пробившись через предыдущие главы, вы в своём квантовом мышлении выросли от младенца до взрослого. Теперь вы понимаете, что такое цвет. Вернёмся к первой фразе этой книги. Почему вишня красная, а черника синяя? Вопрос в том, чтó придаёт цвет предметам и чтó делает вещи разноцветными. Ответ в том, что вещество состоит из атомов и молекул. В отличие от классической механики, где энергия меняется непрерывным образом, атомы и молекулы обладают дискретными уровнями энергии. Свет тоже не непрерывен. Он поступает дискретными пакетами, которые называются фотонами. Фотон имеет определённую энергию, а значит, и определённый цвет. Поскольку энергия должна сохраняться, фотоны могут поглощаться атомами и молекулами, составляющими материю, только когда энергия фотонов совпадает с разницей в энергии между двумя атомными или молекулярными квантовыми энергетическими уровнями. При таком совпадении фотон может поглотиться, и тогда система переходит с низшего энергетического уровня на более высокий. Фотоны, которые не соответствуют разности энергетических уровней, отражаются от предмета. Поэтому если интервалы между энергетическими уровнями молекул таковы, что поглощается красный свет, то синий отражается и объект выглядит синим. Если же интервалы между энергетическими уровнями таковы, что поглощает синий свет, тогда отражается красный свет и объект выглядит красным.

Энергетические уровни и цвета связаны с волновой природой частиц

Занявшись вопросом о цвете предметов немного подробнее, мы в главе 8 обсудили одномерную задачу о частице в ящике. Мы узнали, что абсолютно малые «частицы» — это не частицы в повседневном, классическом смысле. В действительности это волны или волновые пакеты, которые более или менее локализованы в пространстве. В задаче о частице в ящике возможны лишь волны определённых форм. В трёхмерной системе, такой как атом водорода, обсуждавшийся в главе 10, формы этих волн намного сложнее, но и тут существуют лишь некоторые формы, называемые орбиталями. Это верно и для более крупных атомов и молекул, где молекулярные электронные волны описываются молекулярными орбиталями. С электронными волнами (волновыми функциями) в атоме или молекуле связаны строго определённые значения энергии, или энергетические уровни. Мы говорим, что энергия квантуется, то есть меняется дискретными шагами. Дискретные квантовые энергетические уровни — это одно из главных отличий квантовой механики от классической. В классической механике энергия меняется непрерывным образом.

Мы решили квантовую задачу о частице в ящике и обнаружили, что энергетические уровни зависят от размера ящика. В большом ящике (в крупной молекуле) энергетические уровни разделены меньшими интервалами, чем в маленьком. Результат, применимый к реальным молекулам, а не только к частице в ящике, состоит в том, что крупные молекулы тяготеют к поглощению света в красной части спектра. Красный свет обладает более низкой энергией, а для крупных молекул характерны относительно небольшие интервалы между энергетическими уровнями. Молекулы поменьше поглощают свет в голубой части спектра, поскольку различие в энергии между молекулярными уровнями у них больше, а голубой свет обладает большей энергией, чем красный. Самые маленькие молекулы, такие как бензол (см. главу 18), поглощают в ультрафиолетовой части спектра. Поэтому они не вызывают поглощения видимого света. Кристаллы из маленьких молекул, таких как нафталин (применяемый против моли), выглядят белыми потому, что они совершенно не поглощают видимый свет. Их энергетические уровни разнесены слишком сильно, и весь видимый свет отражается от таких кристаллов, отчего они выглядят белыми. По той же причине кристаллы соли в солонке белого цвета, и белый цвет кристаллов сахара тоже связан с этим. И соль, и сахар имеют большие интервалы между энергетическими уровнями и поглощают свет в ультрафиолетовом диапазоне, а цвета видимого света отражают.

Квантовые механизмы скрепляют атомы между собой и определяют форму молекул

Мы знаем, что удерживает атомы в молекулах, что придаёт молекулам их форму и почему форма молекул так важна. Мы видели, что электронные волны атомов объединяются и порождают молекулярные орбитали. Совместное использование электронов атомами на молекулярных орбиталях может приводить к образованию химических связей, которые скрепляют атомы в молекулах. В главах 12–14 мы довольно подробно рассматривали молекулярные орбитали. Выяснилось, что они бывают двух типов: связывающие и разрыхляющие. Размещая электроны надлежащим образом на простой диаграмме энергетических уровней молекулярных орбиталей, можно получить большое количество информации.

В молекуле водорода (см. главу 12) два электрона от двух атомов водорода занимают молекулярную орбиталь с наименьшей энергией, которая является связывающей МО. В результате образуется ковалентная связь, в рамках которой атомы совместно используют пару электронов. Но те же соображения позволяют нам понять, почему не существует двухатомной молекулы гелия. Каждый атом гелия вносит в гипотетическую двухатомную молекулу по два электрона. Первые два из них занимают связывающую МО, но в силу принципа запрета Паули другие два электрона должны занять разрыхляющую МО. В совокупности это приводит к отсутствию связи, и молекулы He2 не существует. Ковалентная химическая связь — это сугубо квантовое явление, не имеющее объяснения в классической механике.

Для атомов крупнее водорода объединение различных s и p атомных орбиталей порождает гибридные орбитали разной формы. Объединение разнообразных гибридных атомных орбиталей в молекулярные орбитали ответственно за тип образующихся связей (одиночных, двойных, тройных) и форму молекул. Мы уделили особое внимание органическим молекулам, то есть молекулам, состоящим в основном из углерода, водорода, кислорода и нескольких других элементов. Органические молекулы важны, поскольку они составляют основу жизни, а также ряда материалов, таких как пластмассы. Выяснилось, что в них очень большое значение имеют типы связей. Молекула легко может вращаться вокруг одиночной углерод-углеродной связи, меняя свою форму, но вращаться вокруг двойной углерод-углеродной связи она не может. Неспособность органических молекул вращаться вокруг двойных углерод-углеродных связей играет ключевую роль в биологии.

В главе 16 мы сконцентрировались на жирных кислотах и жирах. Здесь двойные связи определяют важнейшие различия. Жирные кислоты с двойными связями не могут менять свою форму вблизи этих связей. Полиненасыщенные жирные кислоты имеют множество двойных связей. У всех встречающихся в природе жирных кислот, за исключением некоторых, вырабатываемых жвачными животными, двойные связи находятся в цис-конформации. Это означает, что молекулы жирных кислот изогнуты вблизи двойных связей. Однако химическая обработка полиненасыщенных жиров, направленная на получение мононенасыщенных жиров, приводит к образованию двойных связей в транс-конформации. Жиры с такими связями называются транс-жирами. Молекулы транс-жиров имеют вблизи двойных связей прямую, а не изогнутую форму. Это различие в форме, которое вызвано квантовомеханическими свойствами ковалентной двойной связи, имеет большое значение для биологической активности этих молекул. Транс-жиры оказывают многочисленные вредные воздействия на здоровье человека.

Формы биологических молекул, таких как белки, играют центральную роль в биологии. Формы молекул определяются квантовомеханическим взаимодействием между атомами, что приводит к образованию различных типов молекулярных орбиталей и связей. Таким образом, процессы жизнедеятельности управляются квантовой механикой.

Углекислый газ является парниковым в силу квантовых эффектов

Мы выяснили, что вызываемый углекислым газом парниковый эффект, который приводит к глобальному потеплению климата, является по природе своей квантовомеханическим. Углекислый газ — это квинтэссенция квантовых эффектов, которые придают ему опасные парниковые свойства. Горячие предметы испускают излучение, которое называется черноте́льным. Цвета этого излучения нельзя объяснить в рамках классической теории. На самом деле выводы классической теории оказались настолько ошибочными, что их назвали «ультрафиолетовой катастрофой», поскольку теория предсказывала, что любой горячий объект должен испускать бесконечное количество энергии в ультрафиолетовой части спектра. Ясно, что никакие объекты не испускают бесконечного количества энергии, так что это был ошеломительный провал классической теории.

В 1900 году Планк впервые использовал идею квантования энергетических уровней электронов в веществе, чтобы объяснить черноте́льное излучение. Он вывел формулу для распределения цветов излучения, испускаемого горячим объектом, которая практически идеально совпала с экспериментальными данными. Чем горячее объект, тем больше он испускает высокоэнергетических фотонов. Однако квантовая теория Планка показала, что количество энергии не бесконечно, и позволила в точности вычислить, сколько испускается излучения каждого цвета. Звёзды очень горячие, поэтому они испускают свет в видимом и ультрафиолетовом участках спектра. В качестве примера на рис. 9.1 показан черноте́льный спектр нашего Солнца. Это обычная звезда средней температуры, и поэтому она выглядит желтоватой. Очень горячие звёзды — голубые, а звёзды, которые холоднее Солнца, — красные.

Наша Земля тоже испускает черноте́льное излучение, но, поскольку в сравнении со звездой она очень холодная, глазом её излучение не увидеть. Спектр черноте́льного излучения Земли изображён на рис. 17.1. Это инфракрасное излучение, то есть оно лежит в длинноволновой (низкоэнергетической) части спектра. Без атмосферы всё черноте́льное излучение, испускаемое Землёй, уходило бы в космос и наш мир был бы намного холоднее — возможно, возможно он был бы слишком холодным для существования человека. Однако атмосфера поглощает часть черноте́льного излучения, захватывая тепло в ловушку, и это согревает Землю. Большая часть этого тепла улавливается благодаря водяному пару, у молекул которого переходы между квантованными вращательными энергетическими уровнями соответствуют очень далёкой инфракрасной области (длинным волнам и низкой энергии).

Ранее мы не упоминали о квантовании вращения, и здесь в игру должна вступить ваша квантовая интуиция. Мы говорили о квантованных электронных энергетических уровнях и квантованных колебательных энергетических уровнях. Классические объекты могут вращаться, как, например, волчок. В классической механике энергия, связанная с вращением, является непрерывной величиной. Закрутите волчок чуть быстрее, и его энергия немного возрастёт. Не должно удивлять, что молекулы в газовой фазе, например молекулы водяного пара в воздухе, могут вращаться, а поскольку они являются абсолютно малыми, их вращательная энергия квантуется. Она может меняться только дискретными шагами. Молекула воды может вращаться с одной скоростью, а затем совершить переход к другой скорости, но она не может вращаться с промежуточными скоростями. Представьте, что это означало бы в применении к большим классическим системам. Вот, например, вы едете на велосипеде. Вы нажимаете педали с одной скоростью, но поехать чуть быстрее вы не можете. Надо сразу совершить дискретный скачок к следующему квантовому вращательному энергетическому уровню. Конечно, с абсолютно большими объектами, энергия которых изменяется непрерывно, такого не происходит.

Водяной пар не поглощает земное черноте́льное излучение вблизи пика его спектра, где испускается наибольшее количество энергии. Однако это делает углекислый газ. Как говорилось в главе 17, молекулы обладают квантованными колебательными уровнями энергии. Молекула углекислого газа CO₂ состоит из трёх атомов, и атом углерода находится в её центре. Это линейная молекула, которая испытывает деформационные колебания. Колебательные движения обладают квантованными энергетическими уровнями, и так случилось, что разница между двумя колебательными энергетическими уровнями CO₂ находится вблизи энергии, соответствующей пику земного черноте́льного излучения. По этой причине молекулы CO₂ в воздухе поглощают значительную часть испускаемого Землёй черноте́льного излучения, которая в противном случае уходила бы в космос. Чем больше в воздухе CO₂, тем меньше испущенной Землёй энергии покидает земную атмосферу. В результате с увеличением содержания CO₂ в воздухе всё больше земного тепла остаётся в атмосфере, и планета нагревается. CO₂ является парниковым газом благодаря двум квантовым явлениям: черноте́льному излучению и квантованию колебательных уровней энергии.

Очень горячие объекты испускают видимое черноте́льное излучение

Что касается черноте́льного излучения, то теперь мы знаем, что всякий раз, видя красное свечение таких объектов, как, например, расплавленная лава, изливающаяся из вулкана, или раскалённый нагревательный элемент в электрической печи, мы наблюдаем черноте́льное излучение. Когда электрическая печь настроена на малую мощность, температура её достаточно низка, чтобы всё черноте́льное излучение испускалось в инфракрасном диапазоне, так что мы не видим его глазом. Если использовать спектрометр или инфракрасный детектор, то можно измерить инфракрасные «цвета» испускаемого излучения. Спектр инфракрасного изучения нагревательного элемента характеризует его температуру. Когда печь переключается на высокую мощность, нагревательный элемент краснеет, поскольку становится значительно горячее. Бо́льшая часть его черноте́льного излучения остаётся в инфракрасном диапазоне, но высокоэнергетическая часть черноте́льного спектра приходится на низкоэнергетическую часть видимого спектра, которой соответствует красный цвет.

Электрический нагрев — квантовое явление

Но почему нагревательный элемент печи вообще становится горячим, когда по нему проходит электрический ток? Несмотря на то что сам нагревательный элемент является макроскопическим объектом, мы в главе 19 узнали, что электропроводность и приводящее к нагреву электрическое сопротивление — это проявления фундаментальных квантовых эффектов. Металлические кристаллы, такие как натрий или медь, имеют электроны на взаимодействующих друг с другом атомных орбиталях. Эти атомные орбитали всех атомов кристалла объединяются и образуют молекулярные орбитали, растянутые на весь размер кристалла. Подобно ароматической молекуле бензола, содержащей шесть электронов на шести делокализованных молекулярных орбиталях, образованных взаимодействующими p-орбиталями углерода (см. главу 18), электроны в металле не связаны с конкретным атомом или парой атомов. Вместо этого МО простираются на всю систему, а электроны свободно по ней перемещаются, будь то молекула бензола или металлический кристалл.

Для бензола взаимодействие шести атомных орбиталей приводитк появлению шести молекулярных орбиталей, которые делокализованы в масштабах молекулы. В бензоле только шесть МО, и энергетические интервалы между ними велики. Но даже в очень маленьком металлическом кристалле содержатся миллиарды и миллиарды атомов, что порождает миллиарды и миллиарды МО. За счёт существования такого большого количества МО интервалы между ними очень малы. В металлах все эти МО образуют полосу квантовых энергетических состояний, называемую зоной проводимости. Каждая из этих МО распространяется на весь кристалл. Однако мы знаем, что такие квантовые состояния — собственные энергетические состояния — могут входить в суперпозицию, порождая электронные волновые пакеты, которые более или менее локализованы в соответствии с принципом неопределённости Гейзенберга. И эти электронные волновые пакеты практически свободно движутся по кристаллу.

Электроны заряжены отрицательно. Когда батарея или другой источник тока присоединяется к куску металла, например к отрезку медного провода, электроны стекают на положительный электрод батареи и вытекают из отрицательного электрода. Электроны ускоряются в направлении положительного полюса батареи, что увеличивает их кинетическую энергию. Однако электроны не единственный тип волновых пакетов, движущихся по металлическому кристаллу. Механические колебания атомов в кристаллической решётке имеют квантованные энергетические уровни. Как и в случае с электронной полосой состояний, в макроскопическом куске металла из-за огромного числа атомов имеется колоссальное число квантованных вибрационных уровней, которые образуют полосу механических энергетических уровней. Квантованные делокализованные механические движения связанных в решётку атомов называются фононами. Эти делокализованные фононные волны объединяются и образуют фононные волновые пакеты, которые распространяются по решётке.

Электронные и фононные волновые пакеты сталкиваются. Такие столкновения называются электрон-фононным рассеянием (см. рис. 19.7). Часть избыточной кинетической энергии, которую электрон приобрёл за счёт ускорения в электрическом поле, передаётся фонону. После рассеяния энергия электрона уменьшается, а энергия фонона — увеличивается. Множество таких актов электрон-фононного рассеяния приводит к тому, что совокупная энергия фононов возрастает.

Механическая энергия — это тепло. Температура есть мера количества кинетической энергии в веществе. Электрон-фононное рассеяние замедляет электроны, и этот эффект мы называем электрическим сопротивлением. Увеличение энергии фононов приводит к повышению температуры металла — он становится горячим. Нагрев куска провода при пропускании по нему электрического тока (проходящими по нему электронами) вызван столкновениями электронных и фононных волновых пакетов. Рассеяние этих двух типов волновых пакетов является принципиально квантовомеханическим эффектом. Чем больше протекающий по металлу электрический ток, тем больше случается столкновений и тем горячее становится металл.

Именно это происходит при включении электрической печи. Когда вы увеличиваете ток (число протекающих электронов), то возрастает и число актов электрон-фононного рассеяния. Как следствие увеличивается количество энергии, переходящей в тепло, что вызывает повышение температуры. Когда металлический нагревательный элемент становится достаточно горячим, он начинает испускать красное свечение, поскольку его черноте́льное излучение переходит в видимую часть спектра. В итоге получается, что включение электрической печи или электрообогревателя, сопровождающееся красным свечением нагревательного элемента, включает в себя множество квантовых явлений. Теперь всякий раз, видя раскалённый докрасна нагревательный элемент, вместо того чтобы пребывать в неведении, подобно младенцу, глядящему на луну, подумайте о квантовых электронных состояниях, электронных волновых пакетах, фононных волновых пакетах, порождающем тепло электрон-фононном рассеянии и, наконец, о черноте́льном излучении. Повседневные наблюдения полны квантовых явлений.

Абсолютно малое

Окружающие нас явления квантовой физики проистекают в конечном счёте из того факта, что размер является абсолютным и абсолютно малые частицы ведут себя совсем не так, как классические, то есть абсолютно большие, объекты. Бейсбольный мяч — это классическая частица. Звуковая волна — классическая волна. Бейсбольные мячи и звуковые волны — большие. В классической механике — теории больших вещей — мы встречаемся с волнами и частицами.

Мы говорили, что свет поступает дискретными пакетами, называемыми фотонами. Описание фотонов и электронов как волновых пакетов принципиальным образом отличается от всего, что встречается в классической механике. Абсолютно малые частицы, такие как фотоны и электроны, — это, как мы выяснили в главах 4–7, не волны и не частицы. Это волновые пакеты. Иногда они ведут себя как волны (при дифракции света на решётке или дифракции электронов на кристаллической поверхности), а иногда — как частицы (фотоны в электрическом эффекте и электроны в электронно-лучевой трубке старых телевизоров). Фактически суть природы абсолютно малых частиц состоит в том, что в действительности они не волны и не частицы, а странного типа сущности, которые одновременно обладают свойствами частиц и волн. Этот дуализм материи выражен в принципе неопределённости Гейзенберга. В отличие от классических объектов, таких как бейсбольный мяч, для электрона и других абсолютно малых частиц нельзя одновременно точно знать положение и импульс (произведение массы на скорость).

В каких же случаях частица является малой и принадлежит к новому миру квантовой физики? Дирак учил нас, что существует минимальное возмущение, сопутствующее любому измерению, возмущение, которое связано с самой природой вещей и от которого никогда не удастся избавиться за счёт совершенствования экспериментальной техники. Если это возмущение пренебрежимо мало, то объект является большим в абсолютном смысле и его можно описывать классической физикой. Однако если минимальное возмущение, сопутствующее измерению, не является пренебрежимо малым, то тогда объект абсолютно мал, а его свойства принадлежат царству квантовой механики. Квантовые свойства абсолютно малых частиц не являются странными — они просто нам незнакомы и неподвластны нашей классической интуиции. Они подобны луне для младенца.

В этой книге были изложены фундаментальные концепции квантовой теории, а затем они были применены к ряду важных повседневных явлений. Вы больше не квантовый младенец.

Глоссарий

Абсолютный размер

Объект велик или мал не по сравнению с другим объектом, но по сравнению с неустранимым минимальным возмущением, которое сопровождает любое измерение. Если это возмущение пренебрежимо мало́, объект является больши́м в абсолютном смысле. Если неустранимое минимальное возмущение не является пренебрежимо малым, то объект абсолютно мал.

Ангстрем

Единица длины, равная 10⁻¹⁰ м (одна десятимиллиардная метра). Ангстрем обозначается символом Å.

Анион

Атом или молекула с отрицательным зарядом, например Cl⁻ (анион хлора). Анион образуется при добавлении одного или нескольких отрицательно заряженных электронов к нейтральному атому или молекуле.

Атомная орбиталь

Название волновой функции (волны амплитуды вероятности), которая описывает распределение вероятности электрона вокруг атомного ядра.

Атомный номер

Число протонов (положительно заряженных частиц) в атомном ядре. Нейтральный атом (не ион) имеет такое же число электронов (отрицательно заряженных частиц), как и протонов.

Вектор

Направленный отрезок, обычно изображаемый в виде стрелки. Вектор — это величина, которая характеризуется абсолютным значением и направлением. Если говорится, что автомобиль движется со скоростью 60 километров в час, то скорость не является вектором. Если говорится, что автомобиль движется со скоростью 60 километров в час на север, то скорость является вектором, поскольку характеризуется значением (60 километров в час) и направлением (на север).

Возбуждённое состояние

Состояние атома или молекулы, которое обладает более высокой, чем минимальная, энергией. Возбуждённое состояние возникает, когда атом или молекула, начиная с состояния наименьшей энергии, поглощает фотон подходящей частоты, чтобы перевести систему на энергетический уровень выше самого низкого, называемого основным состоянием. Возбуждённые состояния могут также порождаться теплом или другими механизмами, передающими энергию атому или молекуле.

Волна амплитуды вероятности

Квантовомеханическая волна (волновая функция), описывающая вероятность обнаружения частицы в определённой области пространства. Волна амплитуды вероятности может принимать положительные и отрицательные значения. Вероятность обнаружить частицу в некоторой области пространства определяется квадратом (строго говоря, квадратом абсолютной величины) волны амплитуды вероятности. Чем больше это значение в некоторой области пространства, тем выше вероятность того, что частица будет там обнаружена.

Волновая функция

Решение уравнения Шрёдингера для конкретного состояния системы, например атома или молекулы. Волновая функция — это волна амплитуды вероятности. Она даёт информацию о возможности обнаружить частицу в конкретной области пространства. Например, волновая функция атома водорода даёт вероятность обнаружения электрона на различных расстояниях и в различных направлениях от ядра.

Волновой пакет

Суперпозиция волн, которые, объединяясь, дают частицу, более или менее локализованную в некоторой области пространства. Суперпозиция волн имеет области конструктивной и деструктивной интерференции. Вероятность обнаружить частицу велика там, где интерференция конструктивна. Суперпозиция волн более или менее локализует частицу в некоторой области пространства. Эта локализация не может быть идеальной в силу принципа неопределённости Гейзенберга.

Гибридные атомные орбитали

Комбинации (суперпозиции) атомных орбиталей, которые порождают новые атомные орбитали другой формы. Гибридные атомные орбитали важны при образовании химических связей. Гибридные атомные орбитали образуются для соединения атомов в молекулы с наименьшей энергией (наиболее стабильные молекулы). Формы молекул определяются формой гибридных орбиталей.

Двойная связь

Химическая связь, в которой две пары электронов совместно используются двумя атомами. Двойная связь сильнее и короче, чем одиночная связь.

Деструктивная интерференция

Волны объединяются (складываются друг с другом) таким образом, что общая амплитуда новой волны убывает. Для волн разной длины деструктивная интерференция происходит только в некоторых областях пространства. Волна может быть большой в некоторых областях за счёт конструктивной интерференции и сходить на нет в остальных местах из-за деструктивной интерференции.

Джоуль

Единица энергии: 1 джоуль (Дж) — это произведение метра на килограмм в квадрате, делённое на секунду в квадрате (Дж=м∙кг²/сек²).

Длина волны де Бройля

Длина волны, ассоциированная с частицей, имеющей массу. Для любой частицы существует длина волны де Бройля. Для больших частиц, таких как бейсбольный мяч, дебройлевская длина волны настолько мала, что ею можно пренебречь. Столь большие частицы никогда не ведут себя как волны. Для малых частиц (электронов и т. п.) длина волны сравнима с их размерами, и поэтому малые частицы могут проявлять волноподобные свойства.

Длина волны

Расстояние, на котором волна повторяется, то есть расстояние от одного пика волны до другого.

Допущение Дирака

Минимальное возмущение сопровождает любое измерение. Это возмущение не является следствием экспериментального метода, но присуще самой природе. Никакое усовершенствование техники не сможет его устранить. Если это минимальное возмущение пренебрежимо мало, то частица является большой в абсолютном смысле. Если оно не является пренебрежимо малым, то частица абсолютно мала. Допущение Дирака было подтверждено многочисленными экспериментами и является ключевой идеей для квантовой теории.

Замкнутая конфигурация электронной оболочки

Для атома имеется определённое число электронов, связанных с ядром, которое соответствует одному из благородных газов, занимающих самую правую колонку в Периодической таблице. Замкнутая конфигурация электронной оболочки чрезвычайно устойчива. Благородные газы называют также инертными, поскольку, имея замкнутую конфигурацию оболочки, химически они практически инертны. Атом может обрести замкнутую конфигурацию оболочки, присоединив или отдав электроны и превратившись в ион либо путём совместного использования электронов с другим атомом в рамках ковалентной связи.

Импульсное собственное состояние

Состояние частицы с точно определённым импульсом. Импульсному собственному состоянию свободной частицы, такой как фотон или электрон, соответствует волновая функция, делокализованная по всему пространству. Импульс может быть точно известен при условии, что положение является совершенно неопределённым. Импульсные собственные состояния могут входить в суперпозицию (складываться друг с другом), образуя волновые пакеты, которые имеют более или менее хорошо определённое положение.

Инертные газы (благородные газы)

Атомы, такие как гелий, неон, аргон и т. п., которые обладают замкнутой конфигурацией электронной оболочки. Они занимают правый столбец в Периодической таблице элементов. Благодаря замкнутой конфигурации оболочки они химически почти полностью инертны. Они не создают связей с другими атомами для образования молекул.

Интерпретация Борна

Описание квантовомеханических волновых функций как волн амплитуды вероятности. Интерпретация Борна, также называемая копенгагенской интерпретацией, утверждает, что квантовомеханические волновые функции, получаемые при решении уравнения Шрёдингера, описывают вероятность обнаружения частицы в определённой области пространства.

Интерференция волн

Объединение двух или большего числа волн, порождающее новую волну. В некоторых областях пространства волны могут интерферировать конструктивно, что приводит к увеличению амплитуды волны, а в других областях пространства они могут интерферировать деструктивно, что приводит к уменьшению амплитуды или обращению её в нуль.

Катион

Положительно заряженный атом или молекула, например Na⁺ (катион натрия). Катион — это ион, образующийся при отрыве одного или нескольких отрицательно заряженных электронов от нейтрального атома или молекулы.

Квантованные энергетические уровни

Энергетические уровни, образующие дискретные ступени, когда энергия не может изменяться непрерывным образом. Атомы и молекулы имеют квантованные энергетические уровни.

Квантовое число

Число, определяющее состояние квантовомеханической системы. Для полного описания состояния системы может потребоваться более одного квантового числа. В атоме каждый электрон имеет четыре квантовых числа: n, l, m и s, которые могут принимать лишь определённые значения. Квантовые числа возникают из математического описания квантовомеханических систем.

Кинетическая энергия

Энергия, связанная с движением. Движущаяся частица обладает кинетической энергией, равной половине произведения её массы на квадрат её скорости: E_k=½m∙V².

Классическая механика

Теория вещества и света, разработанная до появления квантовой механики. Рассматривает размер как относительную величину и не может описывать абсолютно малые частицы (электроны, фотоны и т. п.). Это мощная теория, которая безупречно работает при описании больших объектов — мостов, самолётов, траекторий ракет.

Классические волны

Волны, подобные волнам на воде или звуковым волнам, которые можно описывать с помощью классической механики. Электромагнитные волны, которые являются описанием света в классической механике, также относятся к категории классических волн. Классическое описание света как волн хорошо работает для радио и других типов волн, но не может корректно описать корпускулярную природу света (фотонов), ответственную за такие явления, как фотоэлектрический эффект.

Ковалентная связь

Химическая связь, которая удерживает атомы вместе за счёт того, что они совместно используют электроны.

Коллапс волновой функции

Состояние системы часто является суперпозицией волновых функций. Каждая волновая функция соотносится с определённым значением наблюдаемой величины, например энергии. Поскольку суперпозиция состоит из множества волновых функций, она ассоциирована с множеством значений наблюдаемой величины. Когда выполняется измерение, система переходит из состояния суперпозиции волновых функций к одной волновой функции с одним значением наблюдаемой величины (например, энергии). Об этом говорят, что измерение вызывает коллапс волновой функции из состояния суперпозиции в чистое состояние с одним значением наблюдаемой величины. Невозможно заранее сказать, в какое состояние сколлапсирует суперпозиция. Поэтому невозможно предсказать, какое значение измеряемой величины будет получено.

Конструктивная интерференция

Волны объединяются (складываются друг с другом) таким образом, что общая амплитуда новой волны возрастает. Для волн разной длины конструктивная интерференция происходит только в некоторых областях пространства. За счёт конструктивной интерференции волна может быть большой в одной области и сходить на нет в остальных местах.

Кулоновское взаимодействие

Взаимодействие между электрически заряженными частицами, которое убывает с увеличением расстояния. Взаимодействие уменьшается обратно пропорционально квадрату расстояния. Кулоновское взаимодействие заставляет противоположно заряженные частицы (такие, как электрон и протон) притягиваться друг к другу; одинаково заряженные частицы, наоборот, отталкиваются (два электрона или два протона).

Молекулярная орбиталь

Волновая функция для молекулы, составленная из комбинации атомных орбиталей (атомных волновых функций), которая распространяется на всю молекулу. Молекулярные орбитали (МО) могут быть связывающими (связывающие МО). Электроны, находящиеся на связывающих МО, уменьшают энергию молекулы. Молекулярные орбитали также могут быть разрыхляющими (разрыхляющие МО). Электроны, находящиеся на разрыхляющих МО, увеличивают энергию молекулы. Для получения устойчивой молекулы на связывающих МО должно быть больше электронов, чем на разрыхляющих МО.

Нанометр

Единица длины, равная одной миллиардной доле метра (10⁻⁹ м).

Неподелённая пара

Пара электронов в молекуле, которая занимает атомную орбиталь, но не участвует в образовании химической связи. Неподелённые пары электронов не используются атомами совместно.

Одиночная связь

Химическая связь, которая удерживает вместе два атома за счёт одной совместно используемой пары электронов.

Оптический переход

Изменение состояния с одного энергетического уровня на другой в атоме или молекуле, вызванное поглощением или излучением света.

Орбиталь

Другое название для квантовомеханической волновой функции, описывающей электрон или пару электронов в атоме или молекуле. Атом обладает атомными орбиталями, а молекула — молекулярными орбиталями.

Основное состояние

Самое низкое энергетическое состояние атома или молекулы. Возбуждённое состояние порождается, когда атом или молекула, находясь в основном состоянии, поглощает фотон с частотой, подходящей для перевода системы на энергетический уровень выше минимального, то есть основного, состояния. Возбуждённое состояние может порождаться теплом и другими механизмами передачи энергии атому или молекуле.

Поглощение света

Процесс, при котором количество света уменьшается, а энергия объекта увеличивается. Свет (фотоны, частицы света) определённой частоты (цвета) заставляет объект перейти в квантовое состояние с более высокой энергией. Это увеличение энергии объекта в точности совпадает с уменьшением энергии света. Поглощение света объектами обусловливает их цвет.

Постоянная Планка

Фундаментальная постоянная квантовой теории, обозначаемая буквой h. Она входит во многие математические уравнения, используемые в квантовой механике. Например, в соответствии с уравнением Е=h∙ν энергия равна произведению частоты (ν) и постоянной Планка. Значение постоянной Планка составляет: h=6,6∙10⁻³⁴ Дж∙сек. Планк ввёл эту постоянную в 1900 году в своём объяснении черноте́льного излучения.

Потенциальная яма

Область пространства, в которой энергия уменьшается вследствие какого-либо типа притягивающего взаимодействия. Яма в земле является гравитационной потенциальной ямой. Мяч падает на её дно, уменьшая свою гравитационную потенциальную энергию. Чтобы поднять мяч из ямы, необходимо затратить энергию. Электроны удерживаются атомами в кулоновской потенциальной яме, то есть за счёт электрического притяжения отрицательно заряженных электронов к положительно заряженным ядрам. Требуется затратить энергию, чтобы оторвать электрон от атома. Затратив достаточное количество энергии, можно поднять электрон из кулоновской потенциальный ямы, созданной притяжением положительно заряженного ядра.

Принцип запрета Паули

Принцип, согласно которому на одной атомной или молекулярной орбитали может находиться не более двух электронов. Если на одной орбитали находятся два электрона, то они должны иметь противоположные спины, то есть разные электронные квантовые чи́сла s (одно +½, а другое −½). Принцип запрета Паули важен при определении структуры Периодической таблицы элементов и свойств атомов и молекул.

Принцип неопределённости Гейзенберга

Нельзя одновременно точно знать импульс и положение частицы. Если импульс частицы известен точно, то её положение совершенно неопределённо, то есть не может быть никакой информации о её местоположении. Если же точно известно её положение, то не может быть никакой информации о величине импульса. В общем случае принцип Гейзенберга утверждает, что положение и импульс могут быть известны только с определённой степенью погрешности. Это неотъемлемое свойство природы, а не следствие измерительных ошибок.

Принцип суперпозиции

«Когда система находится в одном состоянии, её всегда можно рассматривать как находящуюся частично в каждом из двух или более других состояний».

В соответствии с этим квантовомеханическим принципом система в конкретном квантовом состоянии может быть описана как суперпозиция (сумма) двух или более других состояний. На практике это обычно означает, что конкретная волновая функция может быть выражена как сумма двух или более других волновых функций. Например, волновые функции для молекул можно образовать как суперпозицию атомных волновых функций. Фотонный волновой пакет можно образовать как суперпозицию импульсных собственных состояний.

Пространственное распределение вероятности

Характеризует вероятность обнаружить частицу, такую как электрон, в различных областях пространства. Пространственное распределение вероятности можно вычислить на основе квантовомеханической волновой функции частицы.

Протон

Субатомная частица, имеющая положительный заряд — одна из фундаментальных составляющих атомов и молекул. Положительный заряд протона равен по величине отрицательному заряду электрона. Атом содержит одинаковое число электронов и протонов, так что в целом он не имеет электрического заряда. Число протонов в атомном ядре, называемое атомным номером, определяет заряд ядра. Разные атомы (элементы) имеют разное число протонов в ядре.

Размер абсолютный

Объект велик или мал в абсолютном смысле в зависимости от того, является неустранимое минимальное возмущение, сопровождающее измерение, пренебрежимо малым или нет. Если минимальное возмущение пренебрежимо мало́, то объект является большим в абсолютном смысле. Если оно не является пренебрежимо малым, то объект абсолютно мал. Абсолютно малые объекты могут описываться квантовой механикой, но не классической механикой.

Размер относительный

Размер, определяемый сравнением одного объекта с другим. Объект может быть велик или мал относительно другого объекта. В классической механике предполагается, что размер является относительным. Классическая механика не может описывать объекты, которые малы в абсолютном смысле.

Световой квант

Отдельная частица света. Фотон.

Свободная частица

Частица, на которую не действуют никакие силы. Движение свободной частицы будет прямолинейным, поскольку отсутствуют силы, такие как гравитация или сопротивление воздуха, которые влияли бы на её траекторию.

Собственное состояние

Чистое состояние системы, ассоциированное с точно определённым значением наблюдаемой величины, которое называется собственным значением. Находясь в энергетическом собственном состоянии, система, такая, например, как атом водорода, обладает строго определённой энергией. Атом водорода имеет множество различных энергетических собственных состояний, которым соответствуют различные значения энергии (собственные значения энергии). Система в импульсном собственном состоянии имеет точно определённое значение импульса. Каждому собственному состоянию соответствует волновая функция. Собственные состояния — это фундаментальные состояния в квантовой теории.

Спектроскопия

Экспериментальное измерение количества света на разных длинах волн, поглощаемого или излучаемого системой атомов или молекул.

Тройная связь

Химическая связь, которая удерживает вместе два атома за счёт трёх совместно используемых пар электронов. Тройная связь короче и сильнее (требует больше усилий для разрыва), чем двойная или одиночная связь.

Углеводороды

Молекулы, состоящие только из углерода и водорода, такие как метан (природный газ) и компоненты нефти.

Узел

Для одномерной волны это точка, где амплитуда волны равна нулю. Для трёхмерной волны это плоскость или другая поверхность, где амплитуда волны равна нулю. При пересечении узла знак волновой функции меняется. В квантовой механике узел волновой функции, описывающей частицу, такую как электрон, — это место, где вероятность обнаружить частицу равна нулю.

Уравнение Шрёдингера

Фундаментальное уравнение квантовой теории. Решение уравнения Шрёдингера для атома или молекулы даёт квантованные энергетические уровни и волновые функции, описывающие амплитуду вероятности обнаружения электрона в разных точках пространства в атоме или молекуле.

Фаза

Положение в пределах одного цикла волны. Пик волны (точка максимальной положительной амплитуды) принимается за фазу 0 градусов (0°), ближайший следующий за ней узел (точка, где амплитуда равна нулю) — это 90°. Фаза 90° — это четверть цикла волны. Фаза 180° соответствует половине цикла. Это точка максимальной отрицательной амплитуды. О двух волнах одинаковой длины говорят, что они сдвинуты по фазе, если их пики не совпадают.

Формула Ридберга

Ранняя эмпирическая формула, описывающая цвета излучения, испускаемого и поглощаемого атомами водорода.

Фотон

Частица света.

Фотоэлектрический эффект

Объяснённый Эйнштейном эффект, при котором одиночная частица света — фотон — выбивает из куска металла один электрон. Эйнштейновское объяснение фотоэлектрического эффекта показало, что свет не является волной, как его описывает классическая электромагнитная теория.

Функция радиального распределения

Математическая функция, которая описывает вероятность обнаружения электрона на определённом расстоянии от ядра атома независимо от направления. Она получается из волновой функции электрона в атоме.

Частица в ящике

Квантовомеханическая задача, в которой частица, такая как электрон, заключена в одномерном ящике с бесконечно высокими непроницаемыми стенками. Энергетические уровни частицы в ящике квантуются, то есть для неё существуют дискретные энергетические уровни. Частица в ящике — это простейшая квантовомеханическая задача, в которой частица заключена в небольшой области пространства и имеет квантованные уровни энергии.

Частота

Число повторов регулярного события в единицу времени. Для волны частота — это число пиков волны, которые проходят мимо за определённое время. Для волн, движущихся с одинаковой скоростью, высокая частота соответствует коротким волнам, а низкая частота — длинным волнам. Длина волны — это расстояние между пиками волны. Для световых (электромагнитных) волн частота равна скорости света, делённой на длину волны.

Черноте́льное излучение (излучение абсолютно чёрного тела)

Свет, испускаемый горячим объектом. Цвет этого света зависит от температуры объекта. Черноте́льное излучение — это первое физическое явление, при описании которого Максом Планком в 1900 году были использованы идеи, которые впоследствии легли в основу квантовой механики.

Электромагнитная волна

Волна, состоящая из электрического и магнитного полей, которые колеблются с одинаковой частотой и распространяются со скоростью света. Электромагнитные волны — это описание света в классической механике. Классическая теория электромагнитных волн полезна в описании многих свойств света и радиоволн, но она не может описать многие явления, такие как фотоэлектрический эффект.

Электрон

Субатомная частица с отрицательным зарядом, одна из фундаментальных составляющих атомов и молекул. Отрицательный заряд электрона равен положительному заряду протона, но противоположен по знаку. Атом содержит одинаковое число электронов и протонов, так что в целом он не имеет электрического заряда. Добавление электрона к атому превращает его в анион с единичным отрицательным зарядом. Отдавая электрон, атом становится катионом с единичным положительным зарядом.

Энергетические уровни

В атомах, молекулах и других квантовых абсолютно малых системах энергия не является непрерывной величиной. Изменения энергии могут происходить только дискретными шагами. Каждое отдельное дискретное значение энергии называется энергетическим уровнем.

Комментарии

1

Сёрен Кьеркегор (1813–1855) — датский философ и писатель. — Примеч. пер.

(обратно)

2

Отождествлять массу и вес не вполне корректно. Масса — это скалярная характеристика, присущая объекту самому по себе, а вес — векторная величина (сила), зависящая от состояния, в котором объект находится. Однако для объектов, покоящихся на поверхности Земли, масса и вес пропорциональны друг другу, и в обиходе между ними часто не делают различия. — Примеч. пер.

(обратно)

3

Строго говоря, эта величина называется размахом колебания, а амплитудой обычно называют половину этой величины, то есть отклонение пиков от среднего уровня. — Примеч. пер.

(обратно)

4

В приведённых примерах в качестве обозначений используются первые буквы английских слов velocity (скорость), distance (расстояние) и time (время). Однако нередко буквы выбираются совершенно произвольно. — Примеч. пер.

(обратно)

5

По вертикали. — Примеч. пер.

(обратно)

6

О таких волнах говорят, что они находятся в противофазе. — Примеч. пер.

(обратно)

7

Эдвард Уильямс Морли (1838–1923) — американский физик и химик, с высочайшей точностью определивший атомную массу кислорода. — Примеч. пер.

(обратно)

8

Колебаться. — Примеч. пер.

(обратно)

9

В нашей стране эта игра носит название «Али-Баба». — Примеч. пер.

(обратно)

10

Более известен в России как Луи де Бройль. — Примеч. пер.

(обратно)

11

Точнее, эти функции (комплекснозначные), заданные на трёхмерном пространстве. — Примеч. пер.

(обратно)

12

За пределами видимого диапазона о цвете излучения можно вести речь лишь условно. Корректнее говорить о длине волны света. — Примеч. пер.

(обратно)

13

На уровне n=5 не показаны девять g-орбиталей, соответствующих l=4. — Примеч. пер.

(обратно)

14

Квантовое число l называется орбитальным и характеризует момент импульса электрона, называемый также угловым моментом. — Примеч. пер.

(обратно)

15

Другой термин — «отталкивание электронных пар». — Примеч. пер.

(обратно)

16

Первый ряд переходных металлов располагается в четвёртом периоде Периодической системы элементов и охватывает элементы от скандия (Sc) до цинка (Zn). Второй ряд переходных металлов располагается в пятом периоде и охватывает элементы от иттрия (Y) до кадмия (Cd). Подробнее они описываются ниже. — Примеч. пер.

(обратно)

17

В оригинале Aufbau procedure (от нем. Aufbau — «строительство, сборка»). В русскоязычной литературе обычно используется термин «правило Клечковского» или, реже, «правило Маделунга». — Примеч. пер.

(обратно)

18

В 2000 году группа финских химиков в университете Хельсинки сумела синтезировать гидрофторид аргона HArF. Это единственное известное на сегодня соединение аргона. Оно очень нестойкое и существует лишь при температурах порядка 10 K. — Примеч. пер.

(обратно)

19

В последние годы вместо термина «разрыхляющая молекулярная орбиталь» всё чаще используется калька с английского «антисвязывающая молекулярная орбиталь». — Примеч. пер.

(обратно)

20

От англ. spin — вращение, вращаться. — Примеч. пер.

(обратно)

21

Молекула диуглерода (C₂) может возникать на короткое время, но она химически очень активна и неустойчива. Диуглерод появляется, например, как промежуточный продукт при горении природного газа. Спектральные линии диуглерода (полосы Свана) придают пламени газовой горелки голубой цвет. — Примеч. пер.

(обратно)

22

Шаростержневые модели молекул являются частным случаем более общего типа моделей, называемых скелетными. — Примеч. пер.

(обратно)

23

Объёмные модели молекул также называют моделями Стюарта-Бриглеба. — Примеч. пер.

(обратно)

24

Строго говоря, этот угол составляет 109,471…°. — Примеч. пер.

(обратно)

25

Эта быстрая реорганизация сети водородных связей лишает смысла всякий разговор о памяти воды, на которую часто ссылаются гомеопаты и околомедицинские шарлатаны. — Примеч. пер.

(обратно)

26

Фолдингом (или укладкой) белка называют процесс самопроизвольного сворачивания аминокислотной цепи белка в уникальную, характерную для неё пространственную структуру. Большинство биологически значимых свойств белков проявляется только в таком сложенном состоянии. — Примеч. пер.

(обратно)

27

Мазут по-английски — heating oil, дословно «топочное масло». Поэтому в английском языке мазут естественным образом встаёт в один ряд с маслом любого вида (oil), бензином (light oil) и нефтью в целом (oil). — Примеч. пер.

(обратно)

28

Точнее, молекула жирной кислоты. В английском языке термин fat (жир) может относиться к жирным кислотам, а не только к состоящим из них триглицеридам (о которых речь в конце главы), как в русском языке. В переводе такое упрощённое словоупотребление сохранено лишь там, где оно не приводит к недоразумениям, то есть в основном в диетологическом контексте. — Примеч. пер.

(обратно)

29

Карбоксильная группа — группа −COOH, характерная для класса карбоновых кислот, к числу которых относятся жирные кислоты. — Примеч. пер.

(обратно)

30

Канола (от англ. canola — Canadian oil) — растительное масло, вырабатываемое в основном из рапса, а также из турнепса. — Примеч. пер.

(обратно)

31

К сожалению, в России на этикетках подсолнечного масла нет информации о содержании разного типа жиров. Поэтому судить о составе можно лишь по отметкам «масло холодного отжима», что означает отсутствие термической обработки и, следовательно, гидрогенизации полиненасыщенных жиров, и «рафинированное», что указывает на обработку, которая устраняет характерные запах и привкус и в то же время значительно повышает содержание в масле насыщенных и мононенасыщенных жиров. Ещё одним косвенным признаком может служить срок хранения. Для рафинированного масла, прошедшего гидрогенизацию, он обычно устанавливается равным 12 месяцам, а для масла холодного отжима, которое не подвергалось гидрогенизации, срок хранения, как правило, короче и составляет от трёх до девяти месяцев. — Примеч. пер.

(обратно)

32

Не путать с внешне похожей гош-конформацией, которая образуется при повороте вокруг одиночной углерод-углеродной связи. — Примеч. пер.

(обратно)

33

В дополнение к сказанному далее в тексте следует отметить, что некоторые ω−3 жирные кислоты (в частности, линоленовая) являются незаменимыми — они необходимы организму, но не синтезируются в нём, а должны поступать с пищей. — Примеч. пер.

(обратно)

34

В дальнейшем будет по-прежнемуиспользоваться традиционный для русскоязычной популярной литературы термин «холестерин». — Примеч. пер.

(обратно)

35

Здесь важно избежать недоразумения. Вся энергия, которую Земля получает за счёт солнечного излучения, в конечном счёте излучается в космос. Вопрос состоит в том, какую равновесную температуру будет при этом иметь поверхность Земли. Если часть её теплового излучения блокируется атмосферой, то температура будет повышаться, пока баланс между притоком и оттоком энергии не восстановится. — Примеч. пер.

(обратно)

36

Part per million (ppm) — частей на миллион по объёму (млн⁻¹) — принятый способ описывать содержание небольших составляющих атмосферного воздуха. — Примеч. пер.

(обратно)

37

Строго говоря, излучение Земли уносит в космос всё что поступает от Солнца, и даже немного больше — добавляется небольшой поток тепла, связанный с остыванием земных недр, он, правда, в две-три тысячи раз меньше связанного с Солнцем. — Примеч. пер.

(обратно)

38

Несмотря на технические трудности, ряд компаний уже наладил выпуск сверхпроводящих кабелей из керамических высокотемпературных сверхпроводников, охлаждаемых протекающим внутри них жидким азотом. Для магистральных линий электропередачи такие кабели слишком дороги, но они уже применяются на электрораспределительных подстанциях и, возможно, послужат средством подведения большой электрической мощности в густонаселённые городские районы. — Примеч. пер.

(обратно)

Оглавление

Предисловие

1. Кот Шрёдингера

  Кот Шрёдингера

  Не так, как при бросании монеты

  Реальные явления могут вести себя подобно шрёдингеровским котам

2. Размер абсолютен

  Размер в повседневной жизни

  Метод наблюдения имеет значение

  Большое или малое — это величина возмущений

  Причинность для больших объектов

  Возмущения, которыми нельзя пренебречь, — это важно

  Возмущение есть всегда

  Нельзя рассчитать будущее — только вероятности

3. Кое-что о волнах

  Что такое волны?

  Волны характеризуются скоростью и частотой

  Океанские волны

  Звуковые волны

  Классические световые волны

  Видимый свет

  Сложение волн — интерференция

  Интерференционные картины и оптический интерферометр

4. Фотоэлектрический эффект и объяснение Эйнштейна

  Фотоэлектрический эффект

  Волновая модель не работает

  Эйнштейн даёт объяснение

  Красный свет выбивает более медленные электроны, чем голубой

  Очень красный свет не выбивает электронов

  С какой скоростью вылетает электрон

5. Свет: волны или частицы?

  Классическое описание интерференции не годится для фотонов

  Новое описание фотонов в интерферометре

  Фотон интерферирует сам с собой

  Фотон может находиться в двух местах сразу

  Наблюдение вызывает непренебрежимо малое возмущение, приводящее к изменению состояния

  Возвращаемся к котам Шрёдингера

  Возвращаемся к фотоэлектрическому эффекту

6. Размеры фотона и принцип неопределённости Гейзенберга

  Частицы имеют длину волны

  Как выглядит волновая функция свободной частицы

  Частица с хорошо определённым импульсом размазана по всему пространству

  Интерференция волн разной длины

  Принцип суперпозиции

  Собственные состояния

  Суперпозиция волн амплитуды вероятности импульсных собственных состояний

  Импульс свободной частицы в состоянии суперпозиции

  Импульс частицы в состоянии суперпозиции определён не вполне чётко

  Где находится частица, когда она пребывает в состоянии суперпозиции по импульсу?

  Волновые пакеты

  Разброс по импульсу и координате

  Принцип неопределённости Гейзенберга

7. Фотоны, электроны и бейсбольные мячи

  Волны или частицы?

  Дифракция света

  Дифракция света демонстрирует волновую природу фотонов

  Электроны в кинескопе ведут себя как снаряды

  При дифракции электроны ведут себя как волны

  Электроны и фотоны — это частицы и волны, а бейсбольные мячи — это лишь частицы

8. Квантовый ракетбол и цвет фруктов

  Частица в ящике — классический случай

  Частица в ящике — квантовый случай

  Значения энергии квантовой частицы в ящике

  Волновая функция должна иметь нулевое значение у стенок

  Узлы — это точки, где волновая функция проходит через ноль

  Значения энергии квантуются

  Дискретный набор энергетических уровней

  Связь результатов для частицы в ящике с реальными системами

  Молекулы поглощают свет определённых цветов

  Цвет фруктов

9. Атом водорода: история

  Спектр солнечного черноте́льного излучения

  Тёмные линии в солнечном спектре

  Спектральные линии водорода

  Боровская теория атома водорода (не вполне совершенная)

10. Атом водорода: квантовая теория

  Уравнение Шрёдингера

  Что уравнение Шрёдингера говорит нам о водороде

  Четыре квантовых числа

  Энергетические уровни атома водорода

  s-орбитали атома водорода

  Пространственное распределение s-орбиталей

  Функция радиального распределения

  Формы p-орбиталей

  Формы d-орбиталей

11. Многоэлектронные атомы и Периодическая таблица элементов

  Водород — особый

  Формы орбиталей важны для атомов крупнее водорода

  Энергетические уровни многоэлектронного атома

  Три правила заполнения энергетических уровней электронами

    Правило 1: принцип запрета Паули

    Правило 2: сначала наименьшая энергия, но без нарушения принципа Паули

    Правило 3 (правило Хунда): спины не спариваются, если это возможно без нарушения правил 1 и 2

  Периодическая таблица элементов

    Структура Периодической таблицы

    Конфигурации с замкнутыми оболочками

    Атомы стремятся образовывать конфигурации с замкнутыми оболочками

    Свойства атомов

    При движении сверху вниз по столбцам атомы становятся крупнее

    При движении слева направо по строкам атомы становятся меньше

    Первый ряд переходных металлов

    Более крупные атомы и лантаноиды с актиноидами

    Большинство элементов — металлы

12. Молекула водорода и ковалентная связь

  Два атома водорода, находящихся далеко друг от друга

  Два атома водорода сближаются

  Приближение Борна-Оппенгеймера

  Длина химической связи — это расстояние, которое обеспечивает наименьшую энергию

  Образование связывающих молекулярных орбиталей

  Связывающие и разрыхляющие молекулярные орбитали

  Расселение электронов по молекулярным орбиталям

  Молекула водорода есть, а молекулы гелия нет

13. Что удерживает атомы вместе: двухатомные молекулы

  Сигма-связи (σ) и пи-связи (π)

  Сигма-орбитали молекул

  Молекулярные пи-орбитали

  Связи в двухатомных молекулах: молекула фтора

  Молекулы неона не существует

  Молекула кислорода: правило Хунда имеет значение

  Молекула азота

  Одиночные, двойные и тройные связи

  Гетеронуклеарные двухатомные молекулы

  Визуальные модели молекул

14. Более крупные молекулы: формы многоатомных молекул

  Формы молекул: тетраэдрический метан

  Форма определяется минимизацией отталкивания между связями

  Неподелённые пары тоже имеют значение

  Молекулы треугольной формы

  Переходящие электроны

  Гибридные атомные орбитали: линейные молекулы

  Гибридные атомные орбитали: треугольные молекулы

  Гибридные атомные орбитали: тетраэдрические молекулы

  Углеводороды с одиночной связью

  Большие углеводороды имеют множество структур

  Двойные и тройные углерод-углеродные связи

  Двойная углерод-углеродная связь — этилен

  Тройная углерод-углеродная связь — ацетилен

15. Пиво и мыло

  Спирты

    При комнатной температуре этанол жидкий, а не газообразный

    Вода образует водородные связи

    Вода — великий растворитель

    Этанол участвует в химических реакциях с кислородом

    Метанол крайне ядовит

  Мыло

    Крупные углеводороды — это масло и жир

    Крупные углеводороды могут иметь много разных структур

    Нефтепродукты и вода не смешиваются

    Строение молекул мыла

    В воде мыло образует мицеллы

    Мыло растворяет жирные загрязнения

16. В жирах важны двойные связи

  Из чего состоят жировые молекулы?

  Насыщенные и ненасыщенные жирные кислоты

  Формы жировых молекул

  Насыщенные, мононенасыщенные и полиненасыщенные жирные кислоты

  Важность двойных связей в жирных кислотах

  Химически модифицированные жирные кислоты

  Частично гидрогенизированные и гидрогенизированные жиры

  Гидрогенизация жиров

  Читайте этикетки

  Транс-жиры

  Природа производит цис-жиры, а химическая обработка — транс-жиры

  Транс-жиры могут быть опасны

  Когда ноль — это ноль

  Омега−3 жирные кислоты

  Триглицериды

  Холестерин

  Вопреки общему мнению, холестерин полезен

  Проблема с холестерином

17. Парниковые газы

  Углекислый газ, образующийся при сжигании ископаемого топлива

  Горение метана: природный газ

  Что такое парниковый газ?

  При сжигании ископаемого топлива выделяется углекислый газ

  Выделяемая энергия и количество углекислого газа

  Сжигание реального ископаемого топлива

  Реальное количество углекислого газа, выделяемого при производстве электричества

  Углекислый газ является парниковым в силу квантовых эффектов

  Черноте́льный спектр Земли

  Поглощение земного черноте́льного излучения

  Почему углекислый газ так важен?

  Почему углекислый газ поглощает именно в этой области?

  Колебательные моды углекислого газа

  Квантовые колебания обладают дискретными уровнями энергии

  Энергия квантовых колебаний

  Деформационная мода CO2 поглощает на пике земного черноте́льного спектра

  Парниковый эффект CO2 является кванотовомеханическим

18. Ароматические молекулы

  Бензол: классический ароматический углеводород

  Где находятся двойные связи?

  Делокализация пи-связей

  Связывающие и разрыхляющие молекулярные орбитали

  Углерод-углеродная связь порядка 1,5

  Бензольные делокализованные молекулярные пи-орбитали

  Поглощение света ароматическими соединениями

  Нафталин с позиций задачи о частице в ящике

19. Металлы, изоляторы и полупроводники

  Металлы

    Делокализация молекулярных орбиталей в металлах

    Кусок металла содержит огромное количество энергетических уровней МО, называемое зоной

    Расселение электронов

    Уровень Ферми

    Как электроны движутся сквозь металл

  Диэлектрики

    Диэлектрики не проводят ток вследствие заполненности зоны

    В диэлектриках широкая запрещённая зона

  Полупроводники

    В полупроводниках запрещённая зона небольшая

  Тепловая энергия влияет на электропроводность металлов

  Фононы — вибрации твёрдого тела

  Электронные и фононные волновые пакеты взаимно рассеиваются

  Электрон-фононное рассеяние приводит к нагреванию металла

  Сверхпроводимость

20. Квантовое мышление

  Опыт учит нас понимать классический мир

  Понимание того, что мы видим вокруг себя, требует некоторого знания квантовой механики

  Энергетические уровни и цвета связаны с волновой природой частиц

  Квантовые механизмы скрепляют атомы между собой и определяют форму молекул

  Углекислый газ является парниковым в силу квантовых эффектов

  Очень горячие объекты испускают видимое черноте́льное излучение

  Электрический нагрев — квантовое явление

  Абсолютно малое

Глоссарий

  Абсолютный размер

  Ангстрем

  Анион

  Атомная орбиталь

  Атомный номер

  Вектор

  Возбуждённое состояние

  Волна амплитуды вероятности

  Волновая функция

  Волновой пакет

  Гибридные атомные орбитали

  Двойная связь

  Деструктивная интерференция

  Джоуль

  Длина волны де Бройля

  Длина волны

  Допущение Дирака

  Замкнутая конфигурация электронной оболочки

  Импульсное собственное состояние

  Инертные газы (благородные газы)

  Интерпретация Борна

  Интерференция волн

  Катион

  Квантованные энергетические уровни

  Квантовое число

  Кинетическая энергия

  Классическая механика

  Классические волны

  Ковалентная связь

  Коллапс волновой функции

  Конструктивная интерференция

  Кулоновское взаимодействие

  Молекулярная орбиталь

  Нанометр

  Неподелённая пара

  Одиночная связь

  Оптический переход

  Орбиталь

  Основное состояние

  Поглощение света

  Постоянная Планка

  Потенциальная яма

  Принцип запрета Паули

  Принцип неопределённости Гейзенберга

  Принцип суперпозиции

  Пространственное распределение вероятности

  Протон

  Размер абсолютный

  Размер относительный

  Световой квант

  Свободная частица

  Собственное состояние

  Спектроскопия

  Тройная связь

  Углеводороды

  Узел

  Уравнение Шрёдингера

  Фаза

  Формула Ридберга

  Фотон

  Фотоэлектрический эффект

  Функция радиального распределения

  Частица в ящике

  Частота

  Черноте́льное излучение (излучение абсолютно чёрного тела)

  Электромагнитная волна

  Электрон

  Энергетические уровни

Комментарии

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38